Особенности строения вещества. Лекция №2. Строение кристаллов

Строение кристаллов
Условием термодинамической устойчивости любого кристаллического состояния при данной температуре является минимум свободной энергии
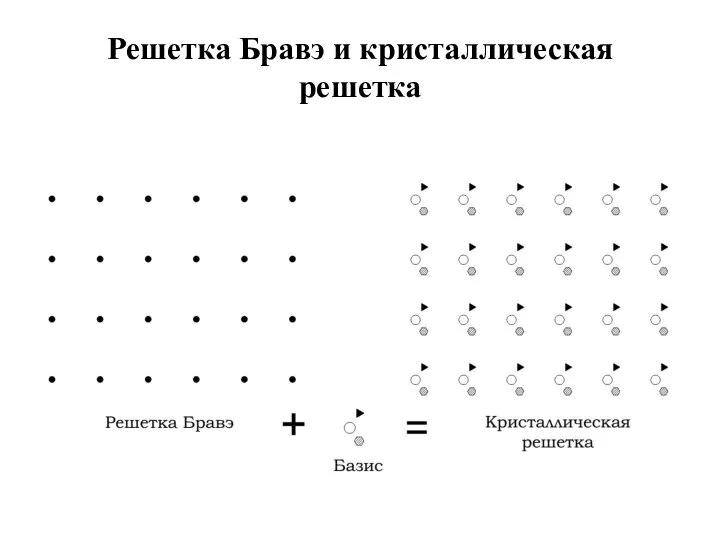
Кристаллическая структура описывается в пространстве с помощью периодически повторяющейся элементарной части кристаллической решетки, называемой элементарной ячейкой, с каждой точкой которой связана некоторая группа атомов, называемая базисом.

Симметрия. Элементы симметрии.
Симметричной фигурой называется такая фигура, в которой отдельные части мысленно могут быть совмещены друг с другом посредством симметричного преобразования.
Точечную группу (класс) симметрии кристаллической решетки можно определить как совокупность операций симметрии, т.е. симметричных преобразований, осуществленных относительно какой-нибудь точки решетки, в результате которых решетка совмещается сама с собой.

Если фигуру повернуть на 180° вокруг линии, перпендикулярной чертежу и проходящей через центр фигуры, то нижняя ее часть совместится с верхней и наоборот. Эта линия называется осью симметрии.
Порядком оси называется число совмещений фигуры при повороте на 360°.

РЕШЕТКИ БРАВЭ

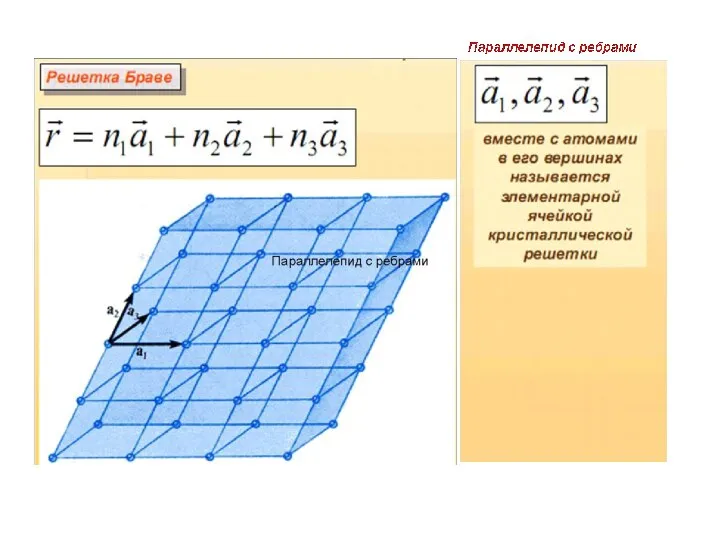
Решетка Бравэ –это бесконечная периодическая структура, образованная дискретными точками и имеющая абсолютно одинаковый пространствен-ный порядок и ориентацию независимо от того, какую точку мы принимаем за исходную.
Число ближайших соседей любой точки решетки Бравэ называется координационным числом.

Решетка Бравэ и кристаллическая решетка

Сингонии кристаллов
Форма элементарной ячейки (соотношение между длинами векторов трансляций и углы между ними) определяет сингонию кристаллов. Различают следующие типы сингоний:

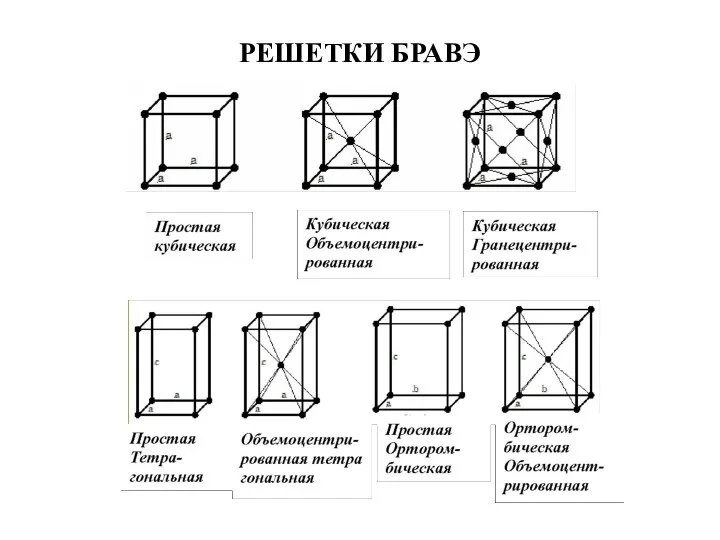
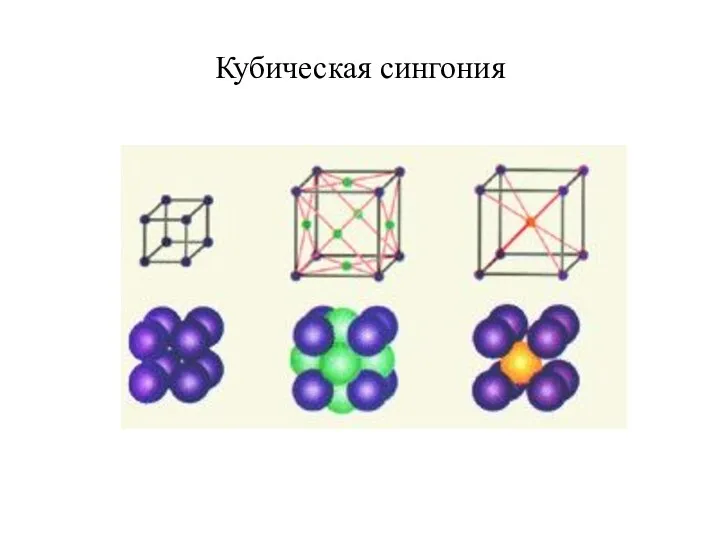
СИММЕТРИИ ПРИМИТИВНЫХ РЕШЕТОК

Кубическая – 3 решетки Бравэ:
Простая кубическая;
Объемноцентрированная
Гранецентрированная
Тетрагональная – 2 решетки Бравэ
Простая тетрагональная
Центрированная тетрагональная
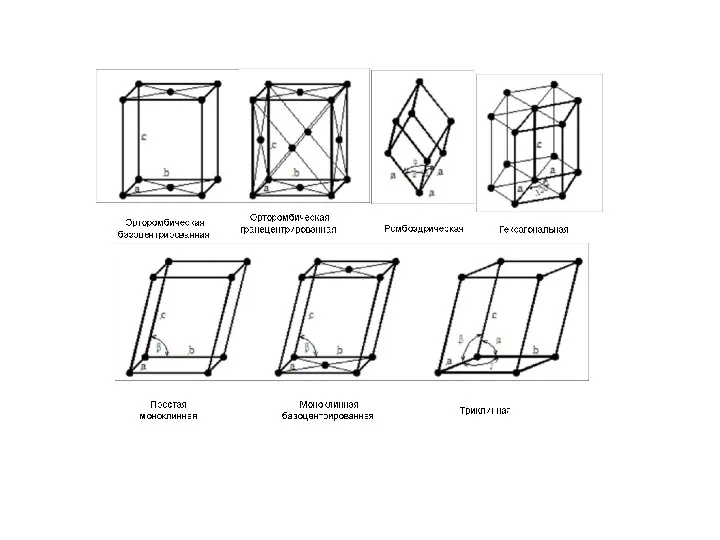
Ромбическая – 4 решетки Бравэ
Простая ромбоэдрическая
Базоцентрированная ромбическая
Объемноцентрированная ромбическая
Гранецентрированная ромбическая
Моноклинная – 2 решетки Бравэ
Простая моноклинная
Центрированная моноклинная
Триклинная - 1 решетка Бравэ
Тригональная - 1 решетка Бравэ
Гексагональная - 1 решетка Бравэ

Кубическая сингония

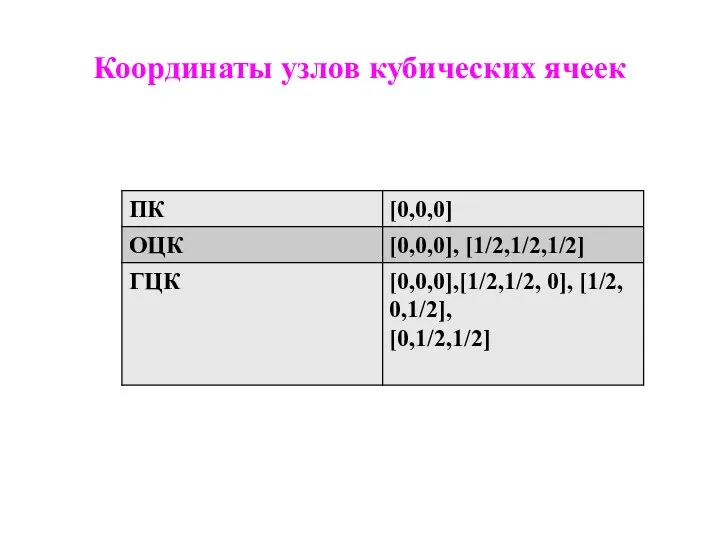
Координаты узлов кубических ячеек

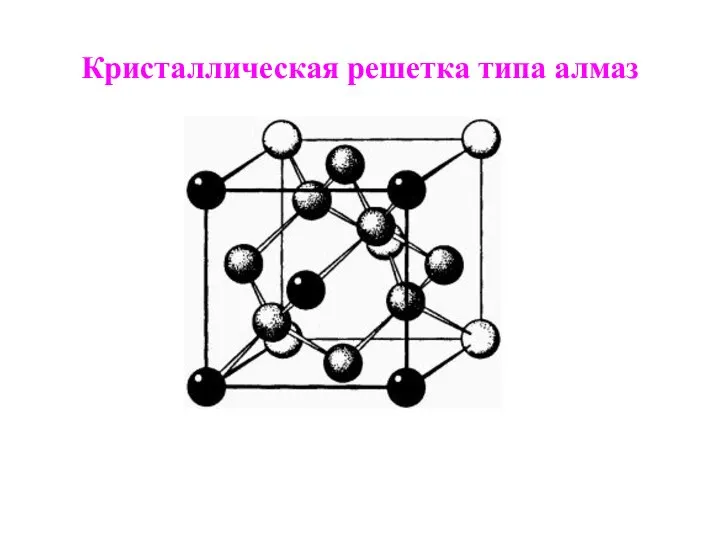
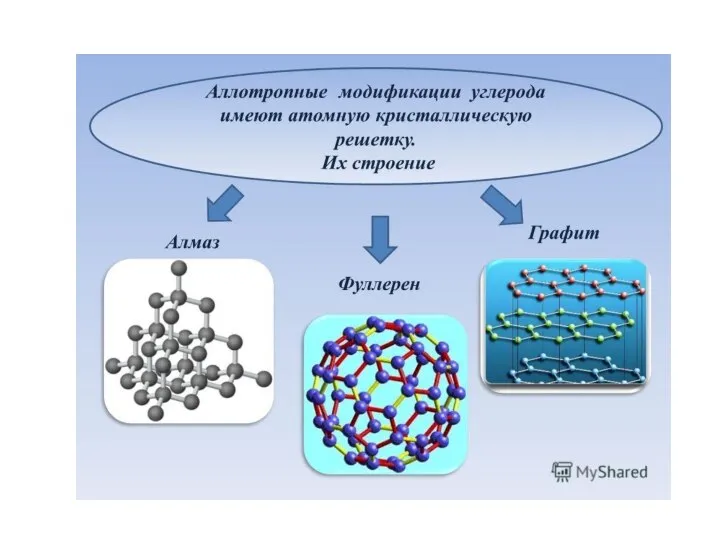
Кристаллическая решетка типа алмаз

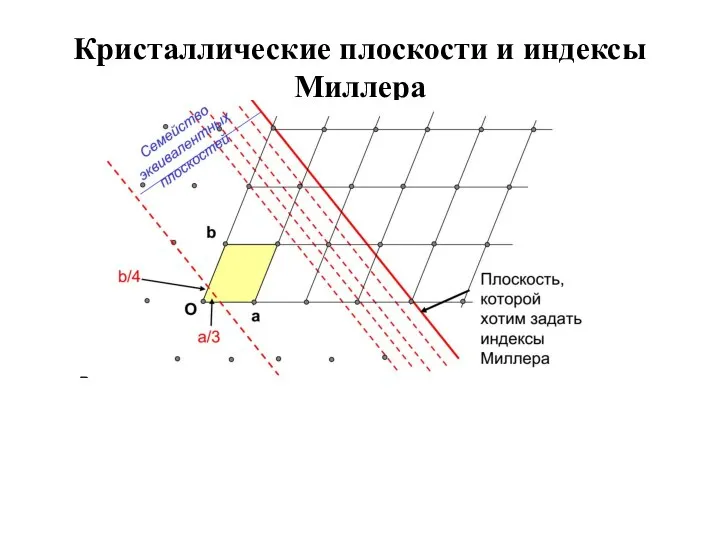
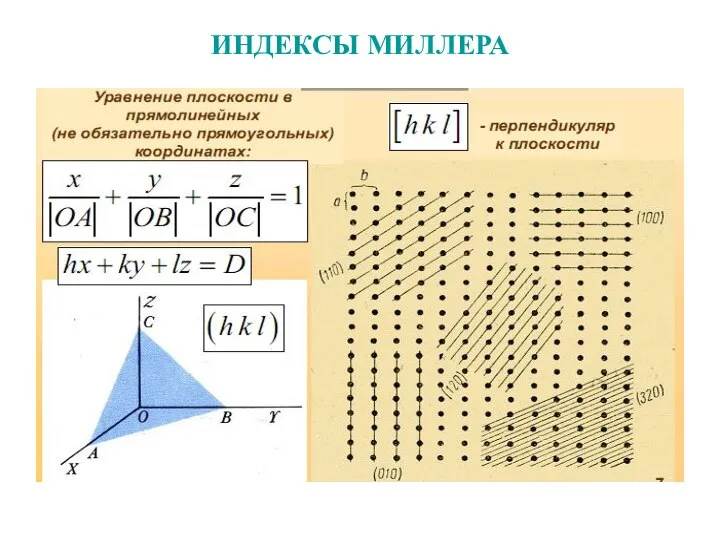
Кристаллические плоскости и индексы Миллера

Кристаллографическое направление – это направление прямой, проходящей через два узла решетки.
Если один из узлов, через который проведена прямая, принять за начало координат, то положение ближайшего к нему узла на прямой, выраженное через числа m,n,p, полностью характеризует положение прямой в кристалле. Координаты этого узла, приведенные к целым числам, заключают в квадратные скобки [mnp] и называют символом направления (ряда) в решетке, а сами индексы m,n,p – индексами Миллера для ряда.

ОБОЗНАЧЕНИЯ

Правила вычисления индексов Миллера

ИНДЕКСЫ МИЛЛЕРА

Индексы Миллера
1) найдем точки, в которых данная плоскость пересекает основные координатные оси, и запишем их координаты в единицах постоянных решетки;
2) возьмем обратные значения полученных чисел и приведем их к наименьшему целому, кратному каждому из чисел.