Слайд 6Доказательство. Единственность решения
Для упрощения записи введем обозначение (а, b):= (х mod p,

x mod q). Вначале покажем, что восстановление исходного значения х вообще возможно, а затем приведем алгоритм его вычисления.
Чтобы вычислить х по заданным (а, b), следует убедиться, что в Zn не существует второго такого числа х', для которого х' mod р = а и х' mod q = b. В противном случае и x и х' привели бы к появлению одной и той же пары (а, b), и ни один алгоритм не смог бы распознать, какое из этих значений является исходным.
Пусть d:= х — х' — это разность чисел, которым соответствует одна и же пара (а, b).
Имеем (d mod р) = (х — х') mod р = (х mod р) — (х'mod p)= =а—а = О, а следовательно, d кратно р.
Аналогичным образом получаем, что d кратно q.
Отсюда следует, что d является кратным НОК(р, q), так как НОК это, наименьшее общее кратное. Поскольку p и q — это неодинаковые простые числа, HОK(p, q) = pq =n, а значит, х — х' кратно n.
Но и x и x' лежат в диапазоне 0,1,... ,n — 1, поэтому разность х - х', кратная n, находится в диапазоне: —n + 1,..., n — 1. Единственным возможным значением такой разности, кратным n, является х—х' = 0, или х = х'. Это доказывает, что для любой заданной пары (а, b) существует не более одного х, удовлетворяющего условиям теоремы. Остается лишь найти значение х.















 ПЛК и безопасность
ПЛК и безопасность Оператор цикла FOR Урок 10
Оператор цикла FOR Урок 10 Понятие информационной системы (ИС)
Понятие информационной системы (ИС) Запоминающие устройства
Запоминающие устройства Мобильные вирусы: миф или угроза
Мобильные вирусы: миф или угроза Массивы в Pascal. Одномерные массивы
Массивы в Pascal. Одномерные массивы Онлайн радиостанция Есть только миг на 101.ру
Онлайн радиостанция Есть только миг на 101.ру 6_1Массивы
6_1Массивы Основные понятия информационных систем, банков и баз данных. Виды учетов в ОВД
Основные понятия информационных систем, банков и баз данных. Виды учетов в ОВД Tensor flow. Smooth dive
Tensor flow. Smooth dive Количество информации. Решение задач
Количество информации. Решение задач Базы данных - основа информационной системы
Базы данных - основа информационной системы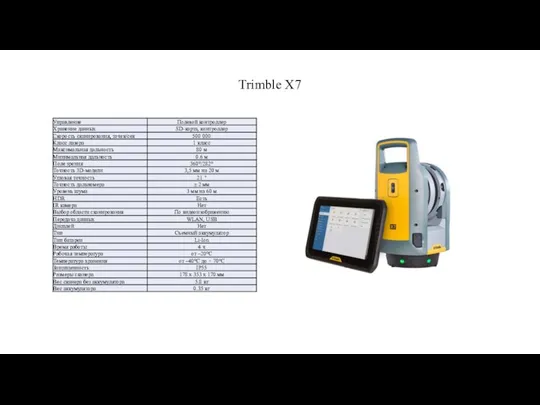 Управление. Хранение данных. Скорость сканирования, точек/сек
Управление. Хранение данных. Скорость сканирования, точек/сек Целеполагание и планирование
Целеполагание и планирование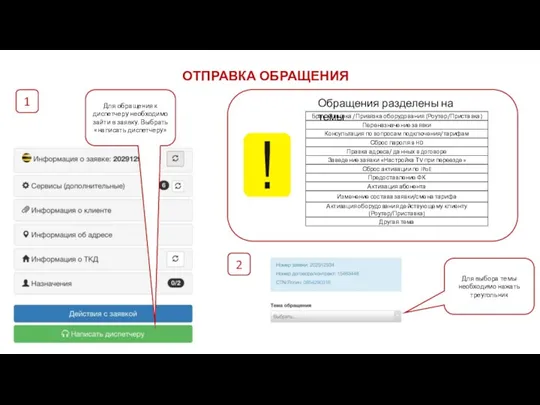 Отправка обращения
Отправка обращения Принципы представления графической информации в ПК
Принципы представления графической информации в ПК Лекция 3-4
Лекция 3-4 СС_8
СС_8 Включение в работу числовых данных. (Урок 5-6)
Включение в работу числовых данных. (Урок 5-6) Отчет по производственной практике Муниципальное образование Илекский сельсовет
Отчет по производственной практике Муниципальное образование Илекский сельсовет История создания смайликов
История создания смайликов Алгоритм. Повторение. Цикл с заданным числом повторений
Алгоритм. Повторение. Цикл с заданным числом повторений Рисуем супер-узоры
Рисуем супер-узоры Шаблон презентации
Шаблон презентации Welcome to Hell - оffice
Welcome to Hell - оffice Нахождение логического выражения по таблице истинности
Нахождение логического выражения по таблице истинности Остросоциальные компьютерные игры
Остросоциальные компьютерные игры Ввод информации в память компьютера. Урок 3
Ввод информации в память компьютера. Урок 3