Алгоритм струны в моделировании травления и осаждения слоев

Вопросы к экзамену
Алгоритм струны в моделировании травления и осаждения слоев.
Расчет процесса травления для заданного показателя анизотропии.
Моделирование процесса литографии. Расчет изображения на поверхности фоторезиста.
Расчет интенсивности освещения в пленке фоторезиста. Моделирование процесса проявления.

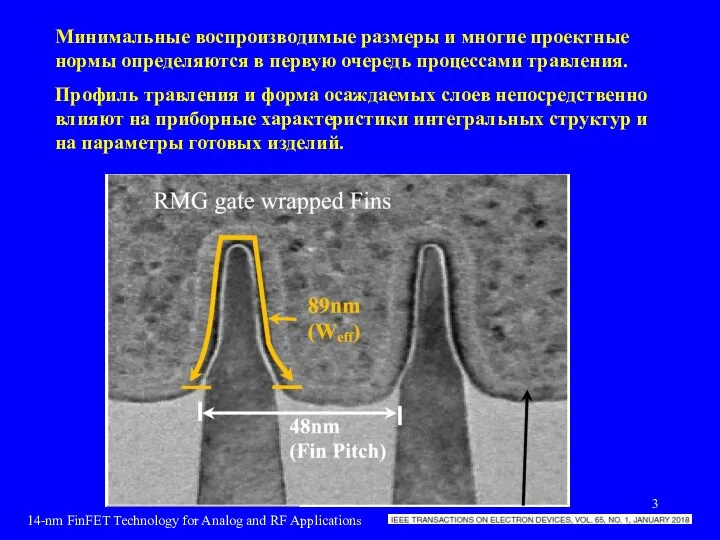
Минимальные воспроизводимые размеры и многие проектные нормы определяются в первую очередь процессами травления.
Профиль травления и форма осаждаемых слоев непосредственно влияют на приборные характеристики интегральных структур и на параметры готовых изделий.
14-nm FinFET Technology for Analog and RF Applications

Выбор моделей травления/осаждения
Следует учитывать трудоемкость процесса разработки высокоточных моделей и программных средств, а также самого вычислительного процесса при расчете каждой задачи, связанной с травлением или осаждением.
При моделировании технологических маршрутов и постановке многофакторных экспериментов на базе «виртуального производства» важной особенностью является очень высокая доля технологических операций травления/осаждения в общей последовательности технологических обработок, в том числе при выполнении операций фотолитографии.

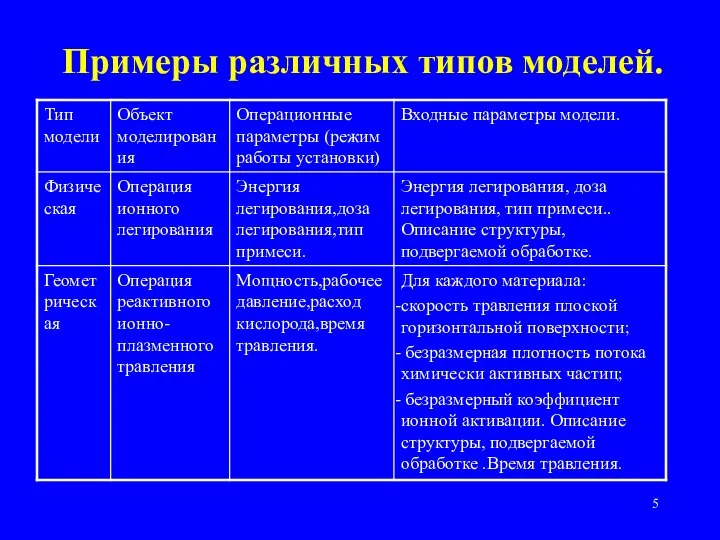
Примеры различных типов моделей.

Особенности использования геометрических алгоритмов
Геометрические модели не учитывают суть происходящих физических и химических процессов, особенности формы и геометрические размеры камеры реактора.
Они оперируют, в основном, с зависимостями скорости травления или осаждения слоя от угла между направлением потока частиц и поверхностью моделируемой структуры в некоторой локальной окрестности.
При правильном выборе параметров такой подход позволяет достаточно точно отображать характер изменения рельефа и рассчитывать временные процессы изменения толщин слоев в интегральных структурах.

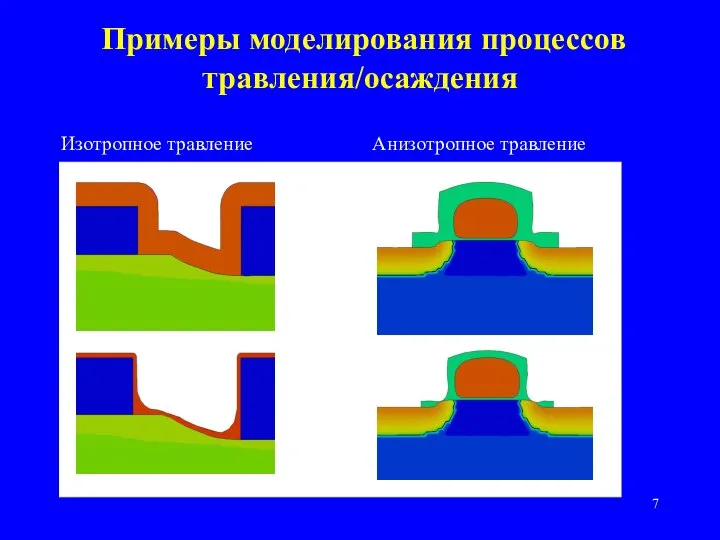
Примеры моделирования процессов травления/осаждения
Изотропное травление
Анизотропное травление

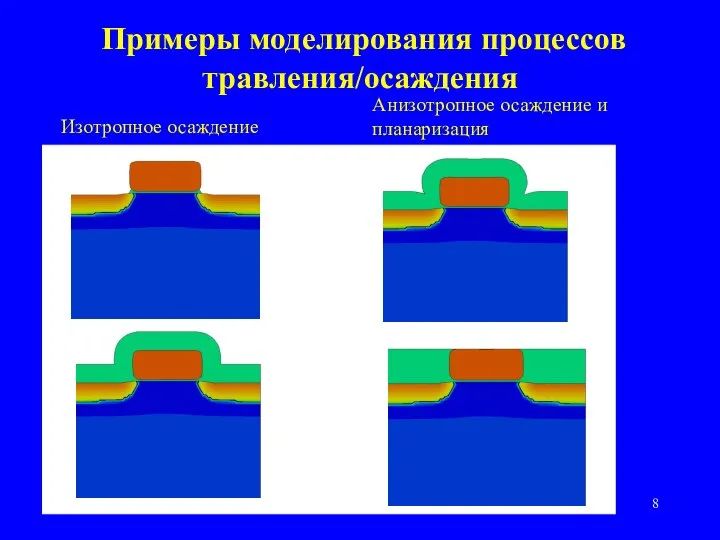
Примеры моделирования процессов травления/осаждения
Изотропное осаждение
Анизотропное осаждение и планаризация

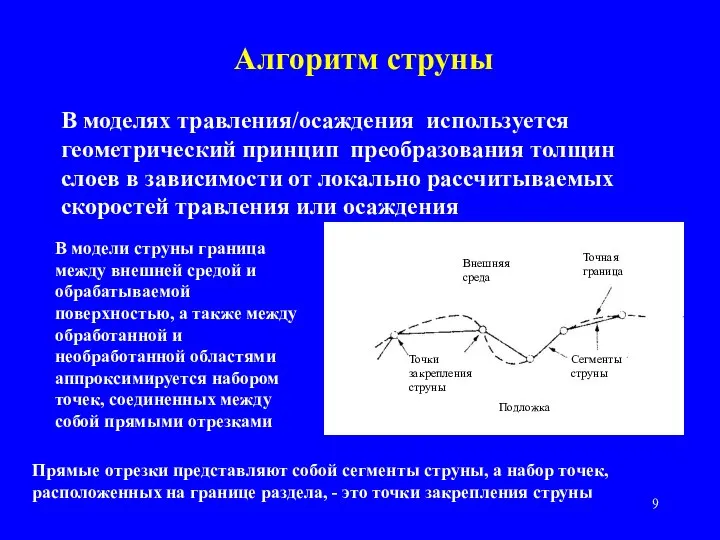
Алгоритм струны
В моделях травления/осаждения используется геометрический принцип преобразования толщин слоев в зависимости от локально рассчитываемых скоростей травления или осаждения
В модели струны граница между внешней средой и обрабатываемой поверхностью, а также между обработанной и необработанной областями аппроксимируется набором точек, соединенных между собой прямыми отрезками
Внешняя среда
Точная граница
Точки закрепления
струны
Подложка
Сегменты
струны
Прямые отрезки представляют собой сегменты струны, а набор точек, расположенных на границе раздела, - это точки закрепления струны

Алгоритм струны (продолжение)
Результирующий профиль обработанной поверхности определяется положением первоначального профиля, который двигается через среду с учетом того, что скорость распространения в каждой точке является функцией локальных переменных.
В каждый текущий момент времени t определяется локальная скорость травления/осаждения в точках закрепления струны;
- по значению локальной скорости рассчитывается перемещение точки за временной шаг Δ t;
- после перемещения точки вновь соединяются прямыми отрезками – сегментами струны, которые составляют результирующее положение фронта травления/осаждения в момент времени t+ Δ t.

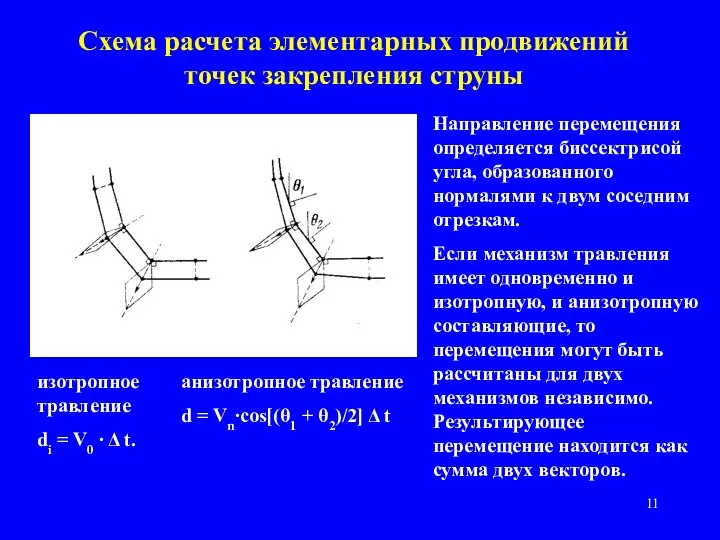
Схема расчета элементарных продвижений точек закрепления струны
изотропное травление
di = V0 ∙ Δ t.
анизотропное травление
d = Vn∙cos[(θ1 + θ2)/2] Δ t
Направление перемещения определяется биссектрисой угла, образованного нормалями к двум соседним отрезкам.
Если механизм травления имеет одновременно и изотропную, и анизотропную составляющие, то перемещения могут быть рассчитаны для двух механизмов независимо. Результирующее перемещение находится как сумма двух векторов.

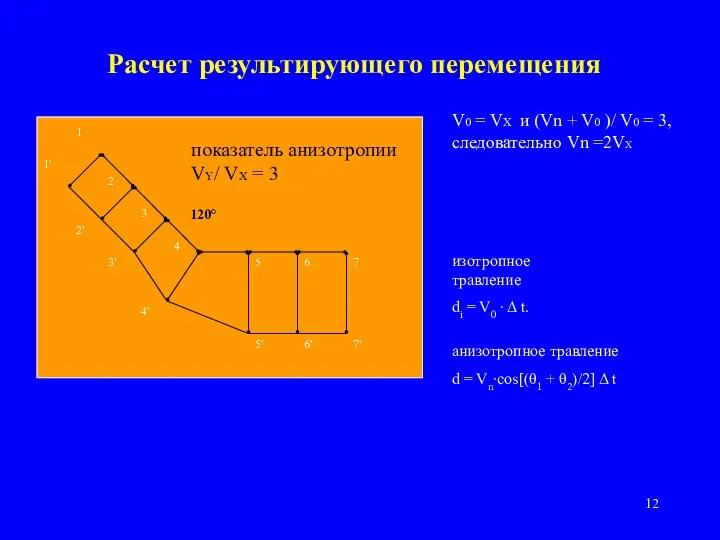
Расчет результирующего перемещения
изотропное травление
di = V0 ∙ Δ t.
анизотропное травление
d = Vn∙cos[(θ1 + θ2)/2] Δ t
показатель анизотропии VY/ VX = 3
V0 = VX и (Vn + V0 )/ V0 = 3, следовательно Vn =2VX

Расчет результирующего перемещения
показатель анизотропии VY/ VX = 3
d1-3 = V0 ∙ Δ t + Vn∙cos[(θ1 + θ2)/2] Δ t =
= V0 ∙ Δ t + 2V0∙cos[(60°+ 60°)/2] Δ t = 2 V0 ∙ Δ t ;
d4 = V0 ∙ Δ t + 2V0∙cos[(60°+ 0°)/2] Δ t = (1+√3) V0 ∙ Δ t ;
d5-7 = V0 ∙ Δ t + 2V0∙cos(0°) Δ t = 3 V0 ∙ Δ t .

Точность алгоритма продвижения струны
Зависит от дискретности представления границы раздела, т.е. от длины сегментов струны
В процессе продвижения фронта длина сегментов может изменяться.
Чтобы избежать такого рода погрешностей, необходимо ввести проверку длины сегментов на каждом новой шаге построения фронта. Если длина какого-либо нового сегмента превышает установленный параметр LMAX, вводится новая точка, и сегмент разбивается на два отрезка

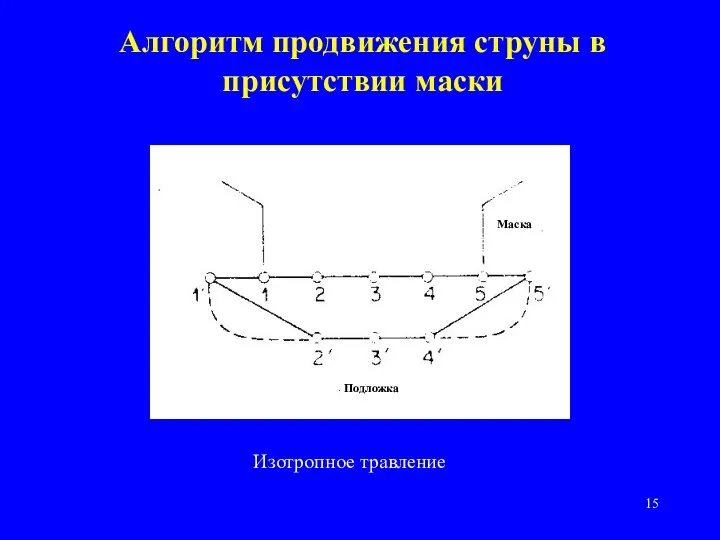
Алгоритм продвижения струны в присутствии маски
Маска
Подложка
Изотропное травление

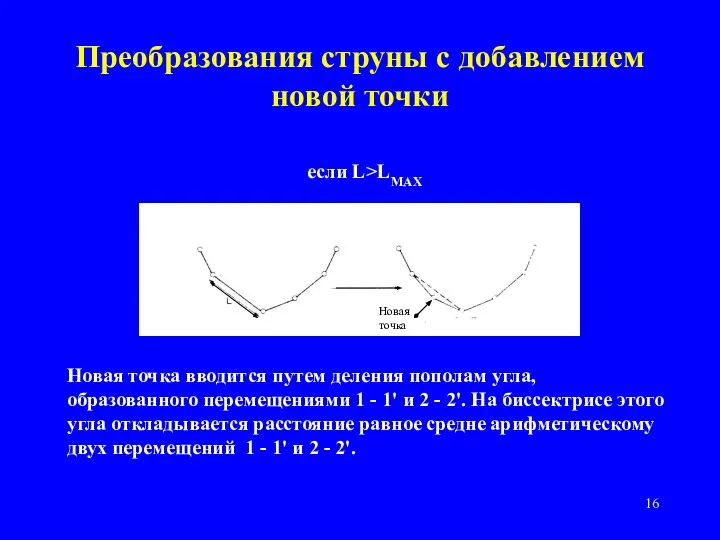
Преобразования струны с добавлением новой точки
Новая точка
Новая точка вводится путем деления пополам угла, образованного перемещениями 1 - 1' и 2 - 2'. На биссектрисе этого угла откладывается расстояние равное средне арифметическому двух перемещений 1 - 1' и 2 - 2'.
если L>LMAX

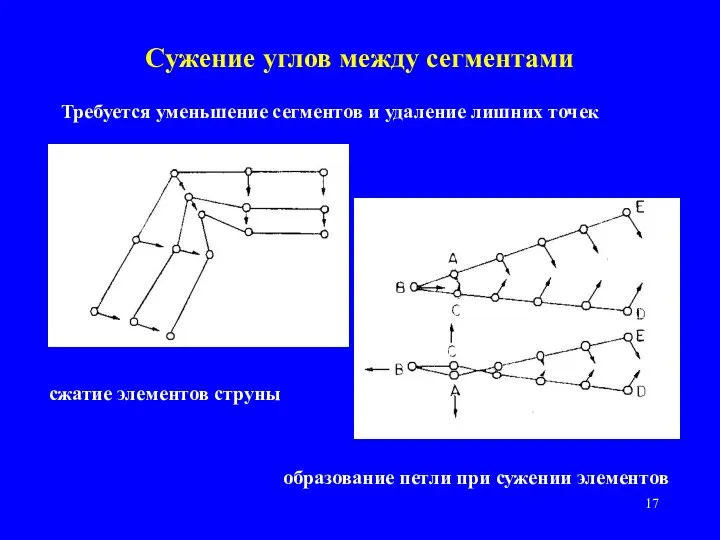
Сужение углов между сегментами
Требуется уменьшение сегментов и удаление лишних точек
сжатие элементов струны
образование петли при сужении элементов

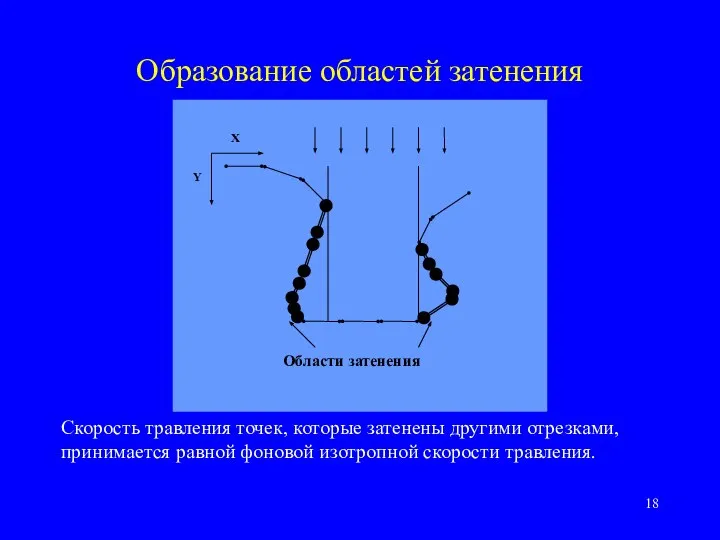
Образование областей затенения
Скорость травления точек, которые затенены другими отрезками, принимается равной фоновой изотропной скорости травления.

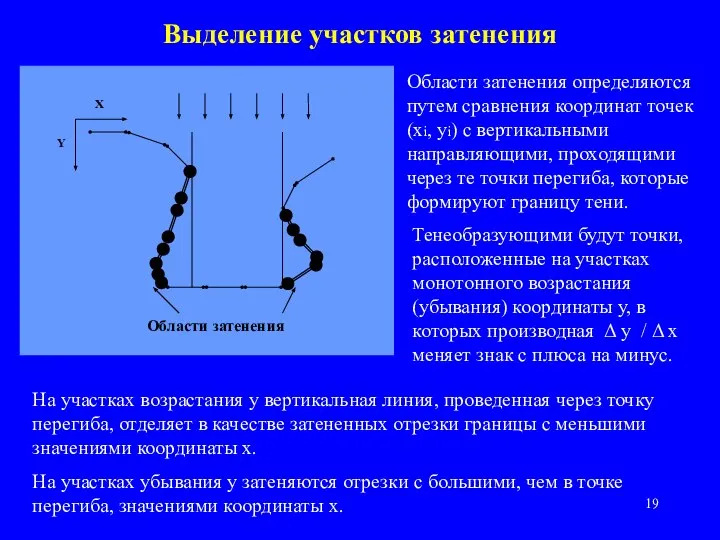
Выделение участков затенения
Области затенения определяются путем сравнения координат точек (xi, yi) с вертикальными направляющими, проходящими через те точки перегиба, которые формируют границу тени.
Тенеобразующими будут точки, расположенные на участках монотонного возрастания (убывания) координаты у, в которых производная Δ y / Δ x меняет знак с плюса на минус.
На участках возрастания y вертикальная линия, проведенная через точку перегиба, отделяет в качестве затененных отрезки границы с меньшими значениями координаты x.
На участках убывания y затеняются отрезки с большими, чем в точке перегиба, значениями координаты x.

Обобщенная геометрическая модель травления
В самом общем случае может быть промоделирован процесс, включающий несколько составляющих скорости травления и несколько потоков травящих частиц, разной интенсивности и направленных под разными углами.
Модель травления на базе разложения в ряд Фурье:
θi – угол между направлением травящего пучка и нормалью к поверхности
factori – относительная интенсивность i-ого травящего пучка
Aj – коэффициенты разложения в ряд Фурье скорости травления как фукции угла θi Для каждого материала может быть задано любое количество коэффициентов Aj.

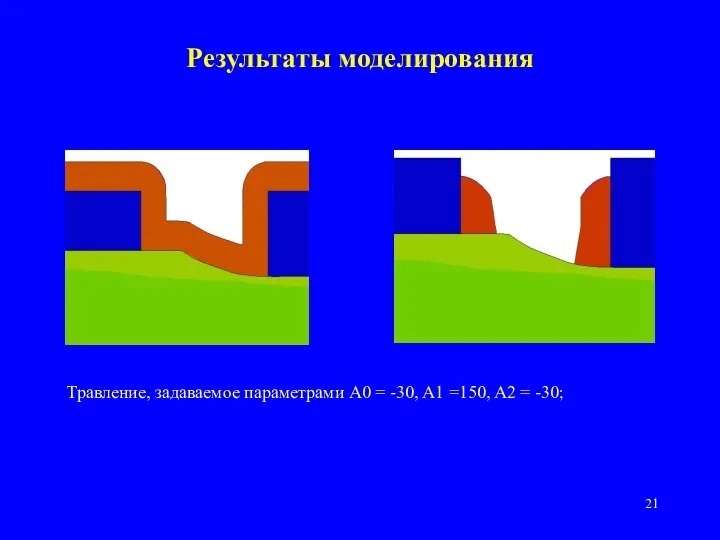
Результаты моделирования
Травление, задаваемое параметрами A0 = -30, A1 =150, A2 = -30;

Моделирование фотолитографии

Цель моделирования фотолитографии
получение расчетного профиля резистивной пленки по краю прорисовки как результата экспонирования и проявления резистивного слоя в ходе соответствующих технологических процессов.
Такой профиль позволяет определять критические размеры элементов, формируемых в резистивной пленке, т.е. ширину линий и зазор, максимальную толщину резистивной пленки, наклон ее края и влияние эффектов стоячих волн на профиль пленки по краю прорисовки.

Основные этапы численного моделирования фотолитографии
расчет распределения интенсивности света, падающего на поверхность резистивной пленки, или фронтального изображения
расчет интенсивности света в пленке как функции глубины
расчет нормализованной концентрации светочувствительного компонента (М) в позитивном резисте как функции координат и времени
определение скорости проявления R(x,y,z) в каждой точке резистивной пленки
расчет процесса проявления с использованием алгоритма продвижения струны

Расчет изображения на поверхности фоторезиста
Распределение интенсивности света на поверхности фоторезиста, называемое также фронтальным изображением, зависит от оптической системы, используемой для проецирования изображения на поверхность
Интенсивность I0 в каждой точке фронтального изображения считается постоянной в течение всего времени экспонирования резистивного слоя. Таким образом, распределение интенсивности света I0 зависит только от координат на поверхности резистивного слоя: I0 = I0(x, y).

Распределение освещенности в плоскости фоторезиста
В идеальном случае интенсивность света должна быть нулевой внутри темных полей или линий и высокой в области зазоров между фигурами. Однако в реальности край изображения никогда не получается идеально резким.
Распределение интенсивности света на краю изображения определяется свойствами источника света и свойствами оптической системы.

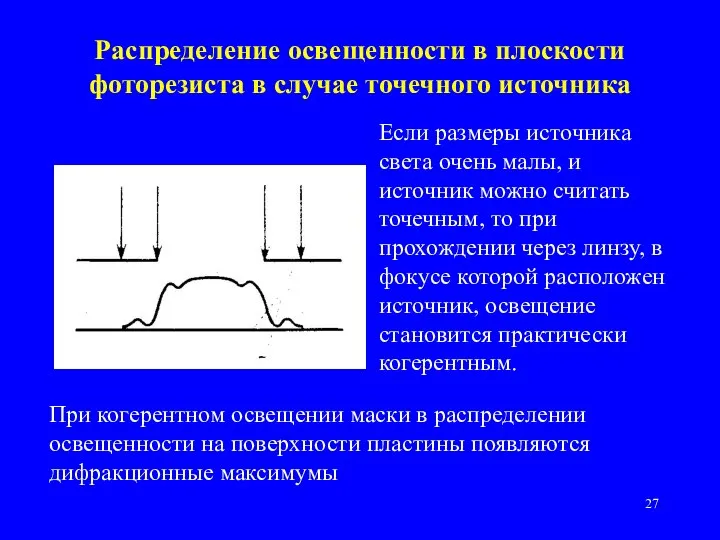
Распределение освещенности в плоскости фоторезиста в случае точечного источника
Если размеры источника света очень малы, и источник можно считать точечным, то при прохождении через линзу, в фокусе которой расположен источник, освещение становится практически когерентным.
При когерентном освещении маски в распределении освещенности на поверхности пластины появляются дифракционные максимумы

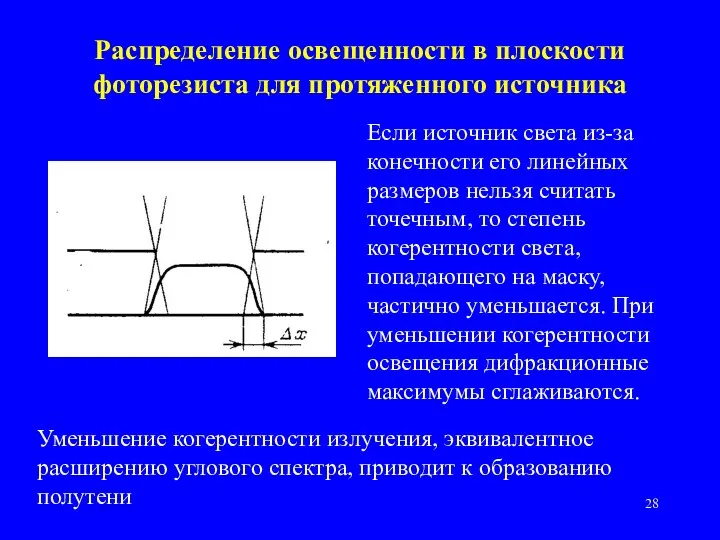
Распределение освещенности в плоскости фоторезиста для протяженного источника
Если источник света из-за конечности его линейных размеров нельзя считать точечным, то степень когерентности света, попадающего на маску, частично уменьшается. При уменьшении когерентности освещения дифракционные максимумы сглаживаются.
Уменьшение когерентности излучения, эквивалентное расширению углового спектра, приводит к образованию полутени

дифракционные максимумы, которые уменьшаются при увеличении размера источника света;
область полутени, которая увеличивается при увеличении размера источника
Два фактора, приводящих к деградации изображения

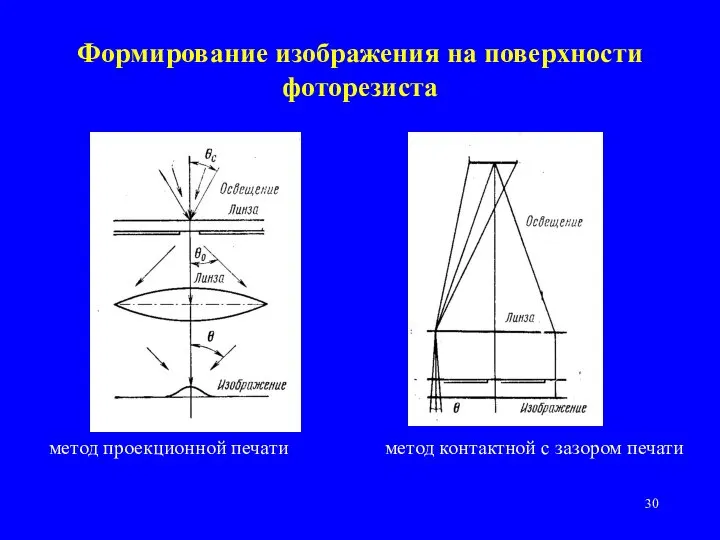
Формирование изображения на поверхности фоторезиста
метод проекционной печати
метод контактной с зазором печати

Параметры, характеризующие маску
Маски амплитудного типа характеризуются функцией пропускания интенсивности T(x, y), такой, что интенсивность освещения, прошедшего через маску, равна
I(x, y) = I0∙ T(x, y),
где I0- интенсивность освещения маски, считающаяся однородной по всей поверхности маски.

Параметры, характеризующие маску
В результате рассеяния на маске каждой из падающих плоских волн образуется спектр когерентных дифрагированных плоских волн. Элементами конфигурации маски являются края и углы прямоугольных прозрачных окон, расположенных на непрозрачном фоне. Предполагая, что стороны прямоугольных окон параллельны осям X и Y системы координат, функцию I(x, y) можно представить в виде разложения в двумерный спектр Фурье:
I(x, y) = ∫∫ J (fX,fY) exp[-2πi (fX∙x + fY∙y)]dfX dfY;
J (fX,fY) = (2π)-2 ∫∫ I(x, y) exp[2πi (fX∙x + fY∙y)]dx dy,
где J (fX,fY) – коэффициенты разложения Фурье для интенсивности освещения, прошедшего через маску, fX, fY – пространственные частоты.

Полная интенсивность I0 уменьшается с глубиной в результате поглощения света резистивным материалом
Отражение света от подложки вызывает наложение стоячих волн в пленке на распределение интенсивности по глубине
Материал резистивного слоя претерпевает химические изменения в процесс экспонирования
Распределение интенсивности по глубине меняется во времени и должно рассчитываться в каждый момент времени отдельно по каждой из имеющихся длин волн
Распределение интенсивности света с длиной волны λ в пленке есть функция трех координат и времени: Iλ = Iλ(x, y, z, t)
Расчет интенсивности освещения в пленке фоторезиста

Физические и химические факторы, учитываемые при расчете распределения интенсивности по глубине
интенсивность освещения на поверхности резистивной пленки
уменьшение интенсивности с глубиной, связанное с поглощением света материалом пленки
отражение света от подложки и возникновение вертикальных стоячих волн
распад светочувствительного компонента в процессе экспонирования (отбеливание фоторезиста) в результате химических реакций и, как следствие, зависимость свойств материала пленки от времени

Моделирование нестационарного процесса отбеливания материала резиста
При моделировании процесса отбеливания позитивного фоторезиста считается, что он имеет комплексный коэффициент преломления, зависящий от нормированной концентрации светочувствительного компонента М и, следовательно, изменяющийся в процессе экспонирования:
n = nr – iλ(A∙M + B)/(4π),
где nr – реальная часть коэффициента преломления, A + B – коэффициент поглощения неотбеленного резиста, B – коэффициент поглощения полностью отбеленного резиста, M изменяется от 1 до 0 в ходе экспонирования. Непосредственно коэффициент поглощения равен
α = A∙M(x, y, z, t) + B.
М - доля светочувствительного вещества, оставшегося в фоторезисте dM/dt = - I(x, y, z, t) ∙ M(x, y, z, t) ∙ C,
где I(x, y, z, t) – локальная интенсивность света, C – чувствительность фоторезиста к отбеливанию

Схема алгоритма анализа прохождения света в тонких пленках
Расчет пропускания и отражения проводится на каждой границе раздела, начиная от поверхности. Определяются комплексные коэффициенты отражения rj и пропускания tj, затем рассчитывается поглощение в каждом тонком слое. Рассчитывается также амплитуда стоячей волны, которая зависит от толщины пленки и оптических коэффициентов. Резист отбеливается (доля светочувствительного вещества М уменьшается) в каждом подслое согласно взвешенной интенсивности и чувствительности С для каждой длины волны, и результаты суммируются по всему спектру длин волн.
На следующем временном шаге t + Δt расчеты повторяются с использованием уже полученных результатов в качестве начальных условий

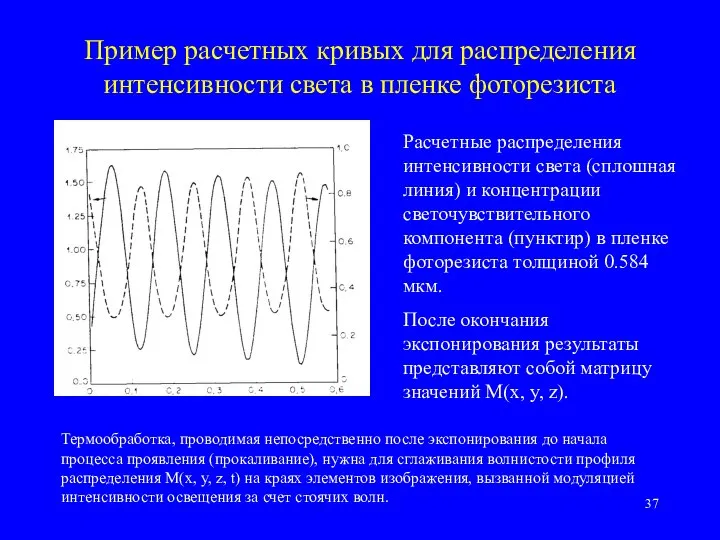
Пример расчетных кривых для распределения интенсивности света в пленке фоторезиста
Расчетные распределения интенсивности света (сплошная линия) и концентрации светочувствительного компонента (пунктир) в пленке фоторезиста толщиной 0.584 мкм.
После окончания экспонирования результаты представляют собой матрицу значений M(x, y, z).
Термообработка, проводимая непосредственно после экспонирования до начала процесса проявления (прокаливание), нужна для сглаживания волнистости профиля распределения M(x, y, z, t) на краях элементов изображения, вызванной модуляцией интенсивности освещения за счет стоячих волн.

Моделирование процесса проявления
Для выполнения расчета профиля резистивной пленки после проявления необходимо задать распределение локальной скорости травления от координат R = R(x, y, z).
Скорость локального травления зависит от концентрации светочувствительной компоненты М, которая одновременно является замедлителем (ингибитором) для реакции растворения пленки. При отбеливании резиста светочувствительная компонента разрушается с выделением органической кислоты, которая является ускорителем в процессе проявления. Можно считать, что доля органической кислоты (ускорителя) пропорциональна (1-М).

Скорость травления химически однородных резистов
1/R(M) = (1-M∙P)/R1 + M∙P/R2 , или
R1 и R2 – скорости травления соответственно полностью отбеленного и неотбеленного материалов,
P = exp[-RS∙(1-M)], RS – безразмерный параметр, характеризующий чувствительность скорости травления к изменению концентрации ингибитора

Полиномиальная аппроксимация скорости травления
R(M) = exp(E1 + E2∙M + E3∙M2).
При использовании таких эмпирических выражений приходится учитывать зависимость значений коэффициентов E1, E2, E3 не только от типа материала резиста, но и от температуры термообработки перед проявлением.
Например, для резиста AZ1350J
E1=5.63, E2=7.43, E3= -12.6, если температура термообработки 70°С, и
E1=4.39, E2=5.69, E3= -9.0, если температура термообработки 100°С.

Типичный профиль края линии в фоторезисте
Расчет процесса проявления методом продвижения струны начинается с поверхности резиста.
Узлы, находящиеся в сильно засвеченной зоне, быстро продвигаются вниз, освобождая центр экспонированного участка, и затем смещаются в стороны к не проявленным зонам, формируя краевой профиль