Алгоритмы и модели трассировки печатных соединений в ЭА

Лекция 8
АЛГОРИТМЫ И МОДЕЛИ ТРАССИРОВКИ ПЕЧАТНЫХ СОЕДИНЕНИЙ В ЭА (часть 1)
1 Трассировка печатных соединений. Постановка задачи
2 Ортогональные алгоритмы трассировки
3 Волновой алгоритм Ли
4 Примеры использования волнового алгоритма

Вопрос 1 Трассировка печатных соединений. Постановка задачи

1) своими координатами (х, у) множество конструктивных элементов
Х = {х1, х2, ..., хt}.
2) множество из L связных подмножеств:
С = {C1, C2, ..., CL},
где каждое l-е подмножество Сl объединяет Nl выводов конструктивных элементов из множества R в соответствии с принципиальной электрической схемой.
3) требования, предъявляемых к топологии платы:
• минимальная ширина проводников и зазора между ними, • размеры контактных площадок, • число слоев металлизации и способы перехода с одного слоя на другой и т. п.
Постановка задачи

с учетом заданных конструкторско-технологических ограничений соединить выводы конструктивных элементов внутри каждого подмножества
Сl ⊂ С
так, чтобы полученные соединения отвечали выбранному показателю качества.
Задача трассировки печатных соединений в общем виде:
1) построение бесперекрестного минимального леса
2) отыскание кратчайшего пути между его вершинами (трассировка соединений).
Требуется

все методы построения минимальных связывающих деревьев не учитывают
- ограничения на размеры монтажного поля
- толщину печатных проводников
- величину зазора между ними.
В результате значительную часть найденных деревьев оказывается невозможным реализовать в виде электрических цепей печатной платы.
Трассировка печатных соединений

Трассировку соединений осуществляют с помощью алгоритмов, основанных на методах динамического программирования.
Общее для алгоритмов - разбиение монтажного поля на ячейки, размер и форма которых определяют плотность и конфигурацию печатных проводников (равносторонние треугольники, квадраты, шестиугольники и др.).
Трассировка печатных соединений

Минимальные размеры ячеек обусловливаются объемом памяти компьютера и соотношением
Трассировка печатных соединений
где d - расстояние между центрами соседних ячеек; bn - минимальная ширина печатного проводника; l -минимальное расстояние между соседними проводниками.
Соединение выводов конструктивных элементов осуществляется в результате последовательного заполнения ячеек трассами, конфигурация которых является локально оптимальной в соответствии с выбранными критериями трассировки.

Вопрос 2 Ортогональные алгоритмы трассировки

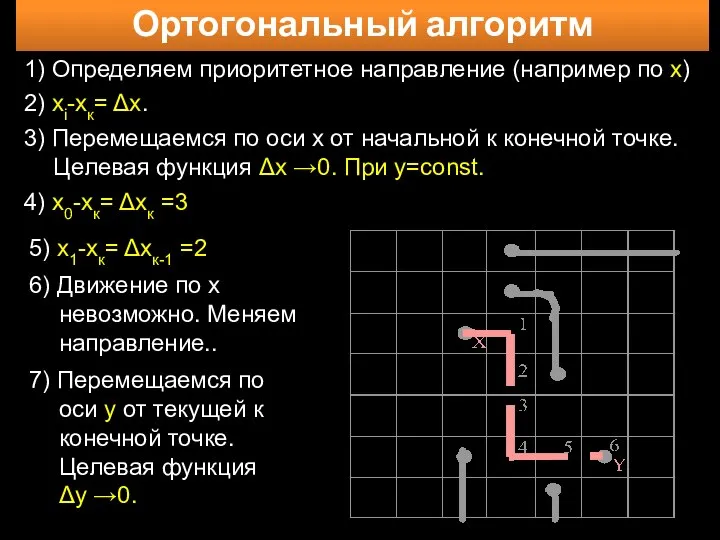
Трассировка печатных соединений по прямым, параллельным осям координат монтажного пространства поочередно для каждой координаты.
При встречи препятствия трасса меняет свое направление на 900. (для МПП – вставляется переходное отверстие)
Достоинства алгоритма:
- обладают самым большим быстродействием
(реализация их на компьютере требует в 75—100 раз меньше вычислений по сравнению с волновыми алгоритмами).
Недостатки алгоритма:
- получение большого числа переходов со слоя на слой,
- отсутствие 100%-ной гарантии проведения ряда трасс,
- большое число параллельно идущих проводников.
Суть:

Ортогональный алгоритм
5) х1-хк= Δхк-1 =2
6) Движение по х невозможно. Меняем направление..
7) Перемещаемся по оси y от текущей к конечной точке. Целевая функция
Δy →0.
5).
1) Определяем приоритетное направление (например по х)
2) хi-хк= Δх.
3) Перемещаемся по оси х от начальной к конечной точке. Целевая функция Δх →0. При y=const.
4) х0-хк= Δхк =3

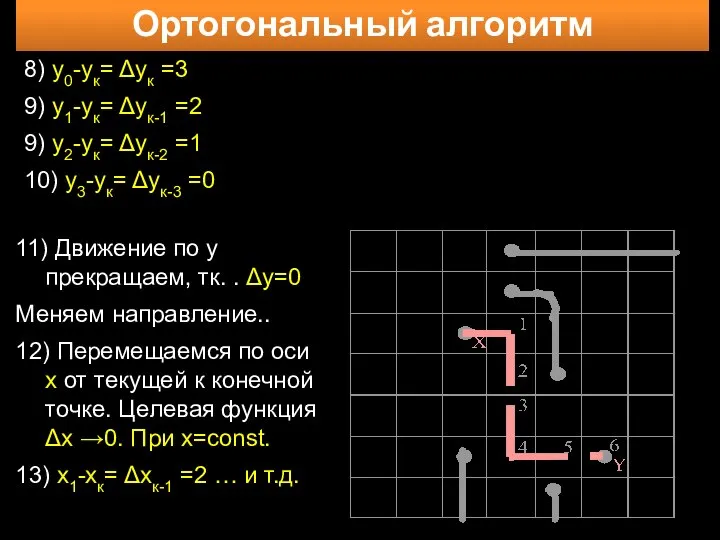
Ортогональный алгоритм
11) Движение по y прекращаем, тк. . Δy=0
Меняем направление..
12) Перемещаемся по оси x от текущей к конечной точке. Целевая функция
Δx →0. При x=const.
13) х1-хк= Δхк-1 =2 … и т.д.
8) y0-yк= Δyк =3
9) y1-yк= Δyк-1 =2
9) y2-yк= Δyк-2 =1
10) y3-yк= Δyк-3 =0

Вопрос 3 Волновой алгоритм Ли

Основные принципы построения
Все ячейки монтажного поля подразделяют на занятые и свободные. Занятые - ячейки, в которых уже расположены проводники, построенные на предыдущих шагах, или находятся монтажные выводы элементов, а также ячейки, соответствующие границе платы и запрещенным для прокладывания проводников участкам.
Остальные - свободные
Для построения трасс возможно использовать только свободные ячейки
На множестве свободных поля моделируют волну влияния из одной ячейки в другую, соединяемых впоследствии общим проводником.

Основные принципы построения
Первую ячейку, в которой зарождается волна влияний, называют источником,
а вторая соединяемая точка - приемник.
Фронту волны влияния на каждом этапе присваивают некоторый вес
где Pk и Рk-1 ‑ веса ячеек k-го и (k‑1)-го фронтов;
Ψ(f1,f2, …,fg) ‑ весовая функция, являющаяся показателем качества проведения пути, каждый параметр которой fi(i = 1, 2, ...,g) характеризует путь с точки зрения одного из критериев качества (длины пути, числа пересечений и т.п.).

Основные принципы построения
Ограничение на вес фронта волны: веса ячеек предыдущих фронтов не должны быть больше весов ячеек последующих фронтов
1) Фронт распространяется только на соседние ячейки, которые имеют с ячейками предыдущего фронта либо общую сторону (хотя бы одну общую точку).
2) Распространения волны продолжается до тех пор, пока ее расширяющийся фронт не достигнет приемника или на i-ом шаге не найдется ни одной свободной ячейки, которая могла бы быть включена в очередной фронт (невозможно провести трассу при заданных ограничениях).
3) При достижении приемника осуществляют «проведение пути» - движении от приемника к источнику по пройденным на этапе распространения волны ячейкам, следя за тем, чтобы значения веса волны монотонно убывали

Основные принципы построения
Для исключения неопределенности при проведении пути (если несколько ячеек имеют одинаковый минимальный вес), вводят понятие путевых координат, задающих предпочтительность проведения трассы.
Каждое направление кодируют двоичным числом по mod q, где q - число просматриваемых соседних ячеек (двухбитным или трехбитным)
Чем меньшее значение путевой координаты - тем более предпочтительно это направление.
Приписание путевых координат производят на этапе распространения волны.
При проведении пути движение от ячейки к ячейке осуществляют по путевым координатам.

Основные принципы построения
Достоинства алгоритма:
- позволяют легко учитывать технологическую специфику печатного монтажа со всей совокупностью конструктивных ограничений.
- всегда гарантируют построение трассы, если путь для нее существует
Недостатки алгоритма:
- невысокое быстродействие;
- большой объем оперативной памяти, необходимый для хранения информации о текущем состоянии всех ячеек коммутационного поля;
- возможность построения лишь соединений типа «вывод - вывод».

Вопрос 4 Примеры использования
волнового алгоритма

Ограничения
Во всех примерах задан приоритетный порядок проведения пути: сверху, справа, снизу и слева:
Проведение пути минимальной длины:
Задано множество ячеек коммутационного поля, на котором построено некоторое число проводников (рис.1).
Построить новый проводник между точками X и Y так, чтобы он не пересекал ранее построенные проводники и имел минимально возможную длину

Проведение пути минимальной длины
Вес ячейки k-го фронта:
Проведение пути начинают с ячейки Y

Проведение пути минимальной длины
4) Процесс продолжаем до тех пор, пока след не приведет в точку X.
1) Просматриваем окрестность точки приемника и находим ячейку, которая в наиболее предпочтительном направлении имеет вес на единицу меньше
2) Перемещаемся в эту ячейку и отмечаем след перехода.
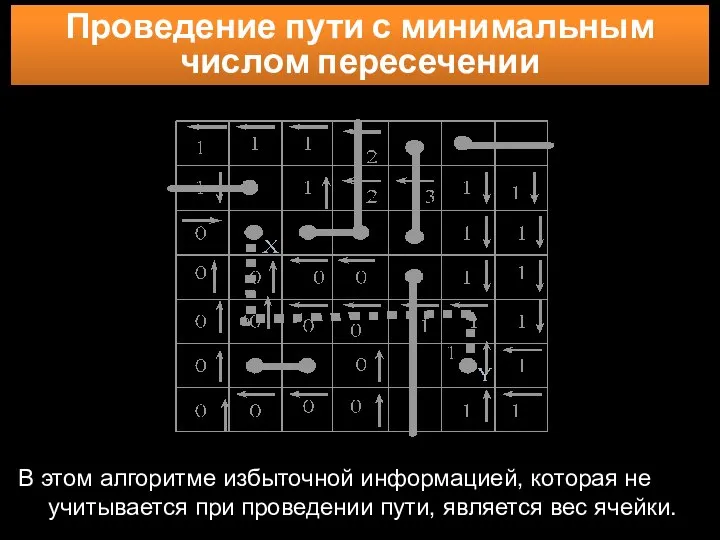
3) …

Проведение пути с минимальным числом пересечении
занятые ячейки: в которых
а) находятся выводы конструктивных элементов,
б) имеются изгибы или пересечения ранее построенных проводников,
в) ячейки, в которых направление проводников совпадает с путевой координатой строящегося пути.
При этом в k-й фронт включаем лишь те ячейки, которые имеют минимальный вес.

В этом алгоритме избыточной информацией, которая не учитывается при проведении пути, является вес ячейки.
Проведение пути с минимальным числом пересечении

Параллельная оптимизация пути по нескольким параметрам
Например:
1) Рk = Pk-1 + 1 если в данной и соседних ячейках нет ранее построенных проводников и путевая координата не меняет своего направления;
2) Рk = Pk-1 + 2, если в соседних ячейках нет ранее построенных проводников, но путевая координата меняет свое направление;
3) Рk = Pk-1 + 4, если в данной ячейке путевая координата не меняет своего направления и нет ранее построенного проводника, но в соседней ячейке такой проводник есть;
4) Рk = Pk-1 + 8, если в данной ячейке происходит пересечение с ранее построенным проводником

Вопросы по прочитанному материалу?