Содержание
- 2. Рекурсия Рекурсивный алгоритм – это алгоритм, в описании которого содержится обращение к самому себе. Рекурсивная функция
- 3. Пример рекурсии. Вычисление факториала static int Factorial(int x) { if (x == 1) { return 1;
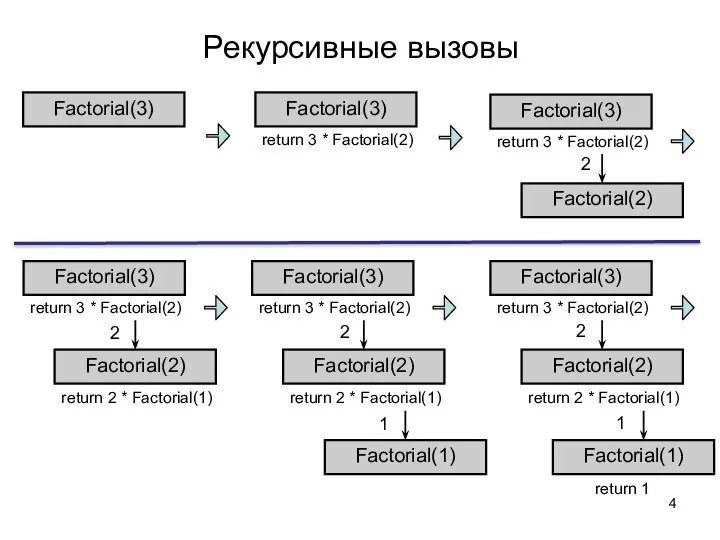
- 4. Рекурсивные вызовы Factorial(3) return 3 * Factorial(2) Factorial(3) return 3 * Factorial(2) Factorial(3) Factorial(2) return 3
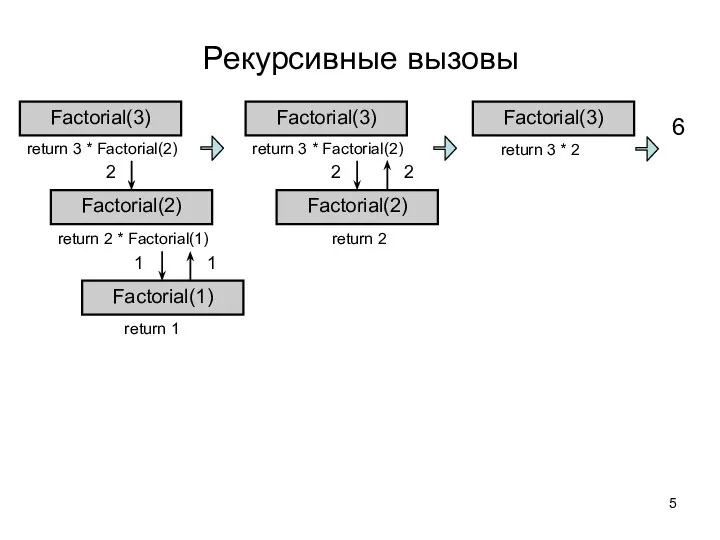
- 5. Рекурсивные вызовы return 3 * Factorial(2) Factorial(3) Factorial(2) return 2 * Factorial(1) Factorial(1) return 1 2
- 6. Построение оценки для рекурсивного алгоритма static int Factorial(int x) Т(n) { if (x == 1) 1
- 7. Методы решения рекуррентных отношений Метод итераций Дерево рекурсии Основная теорема
- 8. Метод итераций На основании формулы T(n) записываем формулу для меньшего элемента, находящегося в правой части формулы,
- 9. Сумма n - первых членов арифметической прогрессии Sn=a1+a2+…+an может быть найдена по формуле где а1 —
- 10. Метод итераций. Вычисление Factorial T(n)=T(n-1)+1, T(1)=1 T(n)=θ(g(n)), g(n)=? T(n-1)=T(n-2)+1 T(n-2)=T(n-3)+1 T(n)= T(n-1)+1= T(n-2)+1+1= T(n-3)+1+1+1=… Т(1) +n-1=
- 11. Сортировка слиянием (merge sort) – асимптотически оптимальный алгоритм сортировки сравнением, основанный на методе декомпозиции («разделяй и
- 12. Разбиваем массив на две половины меньшего размера, пока размер массива больше 1 2. Рекурсивно сортируем каждую
- 13. void mergeSort (int a[], int l, int r) { int mid; if (l mid = (l
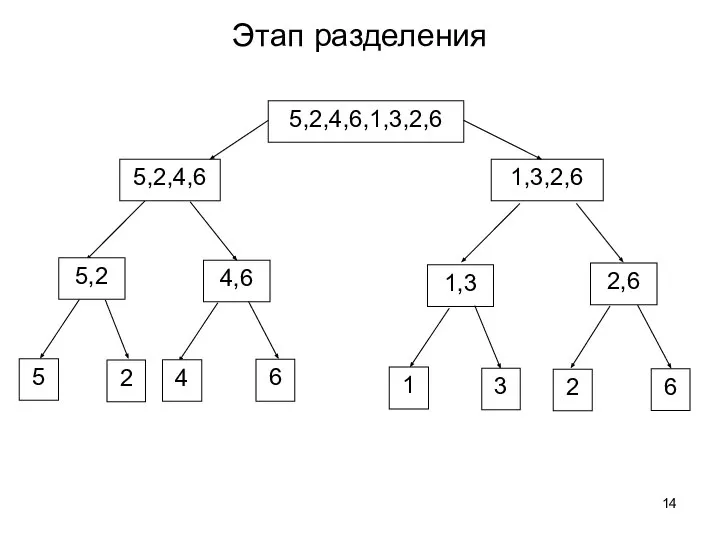
- 14. Этап разделения
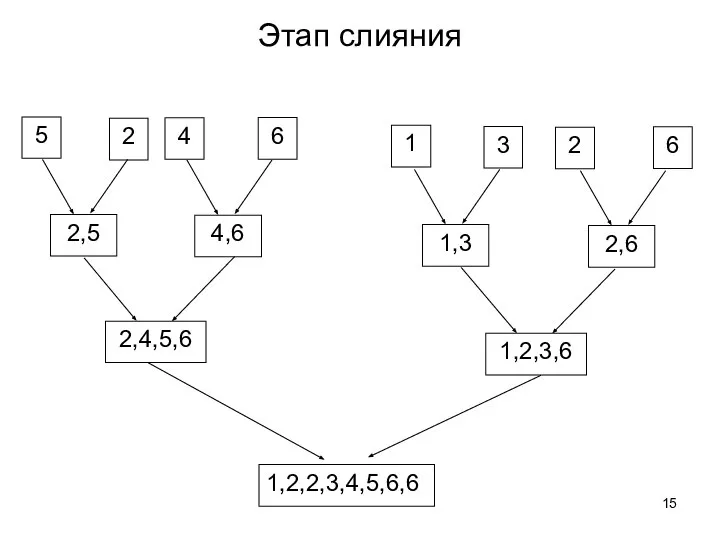
- 15. Этап слияния
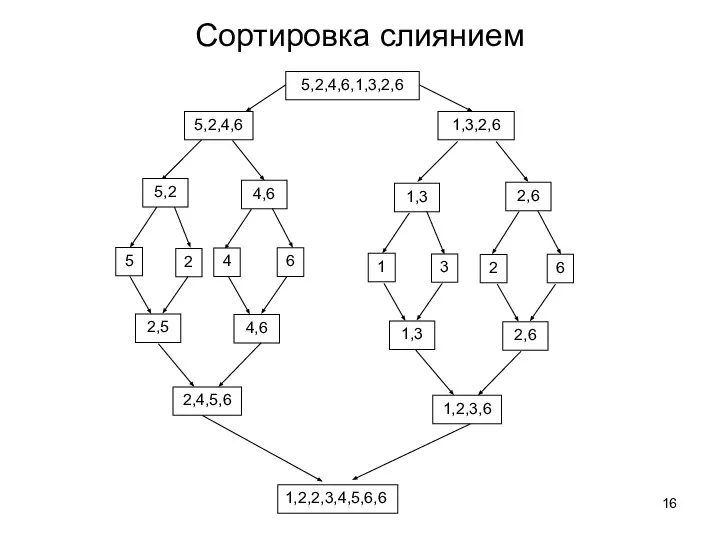
- 16. Сортировка слиянием
- 17. A1: 3, 4, 6, 11 A2: 2, 5, 7, 8 A: 2 2 A1: 3, 4,
- 18. void mergeSort (int a[], int l, int r) { T(n) int mid; 1 if (l mid
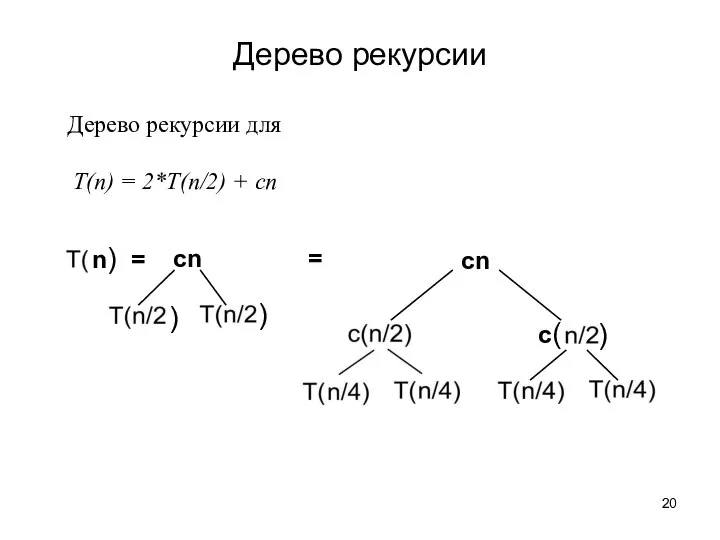
- 19. Рекуррентное соотношение - это соотношение содержащее функцию Т(n) в левой и правой части выражения Дерево рекурсии:
- 20. Дерево рекурсии для T(n) = 2*T(n/2) + cn Дерево рекурсии
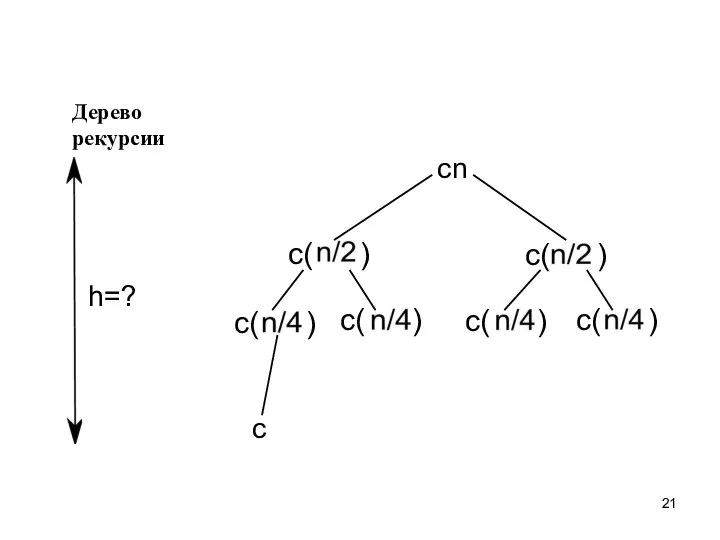
- 21. Дерево рекурсии
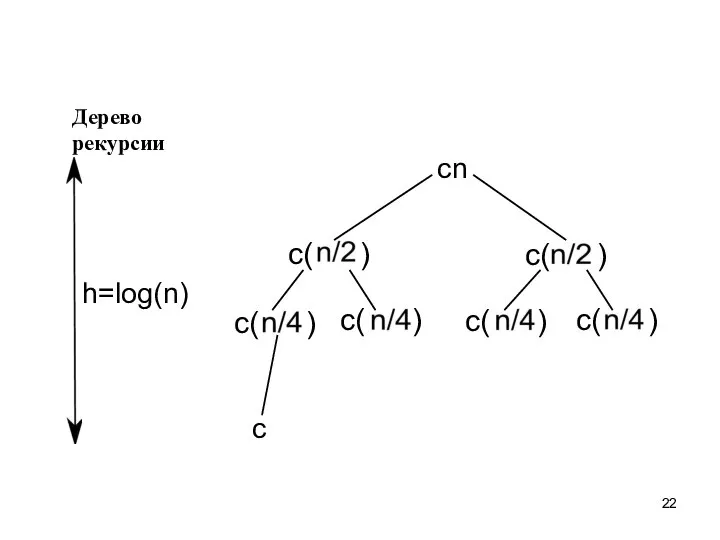
- 22. Дерево рекурсии
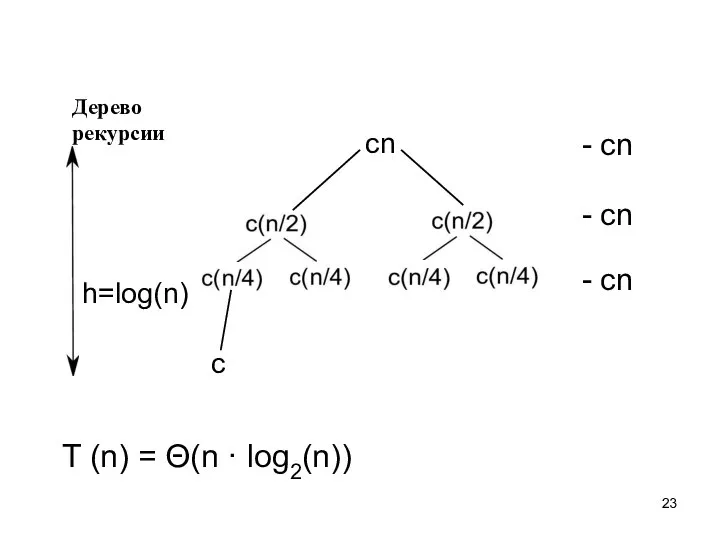
- 23. T (n) = Θ(n · log2(n)) Дерево рекурсии
- 24. Сравнение алгоритмов сортировки Сортировка вставками – Θ(n2) Сортировка слиянием - Θ(n * log2(n))
- 25. Дерево рекурсии Дерево рекурсии - графический метод, который отображает разворачивание рекуррентного соотношения в систему рекурсивных вызовов
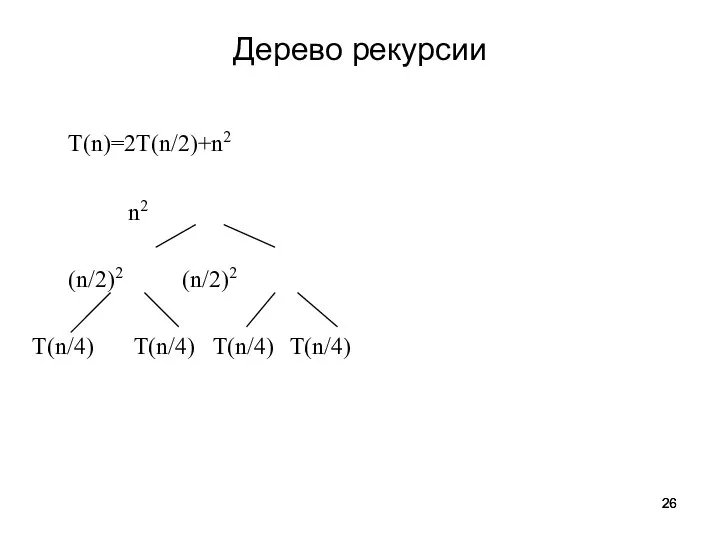
- 26. Дерево рекурсии T(n)=2T(n/2)+n2 n2 (n/2)2 (n/2)2 T(n/4) T(n/4) T(n/4) T(n/4)
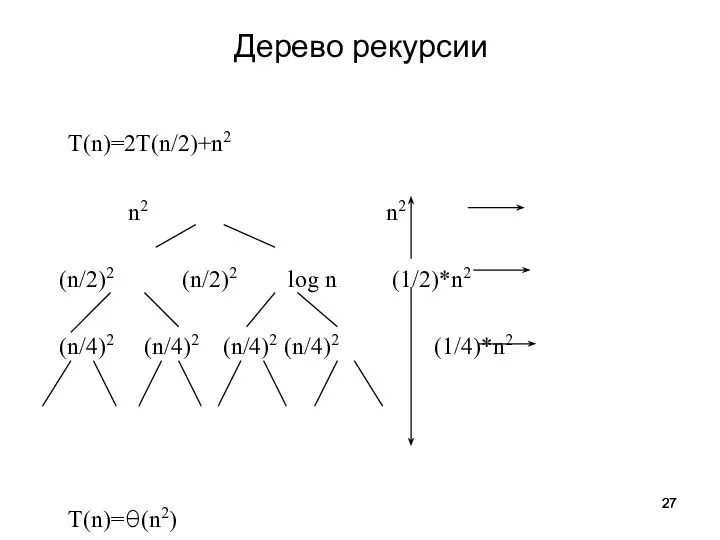
- 27. Дерево рекурсии T(n)=2T(n/2)+n2 n2 n2 (n/2)2 (n/2)2 log n (1/2)*n2 (n/4)2 (n/4)2 (n/4)2 (n/4)2 (1/4)*n2 T(n)=θ(n2)
- 28. Сумма: по уровням (1 + 1/2 + 1/4 + . . . + 1/2k + .
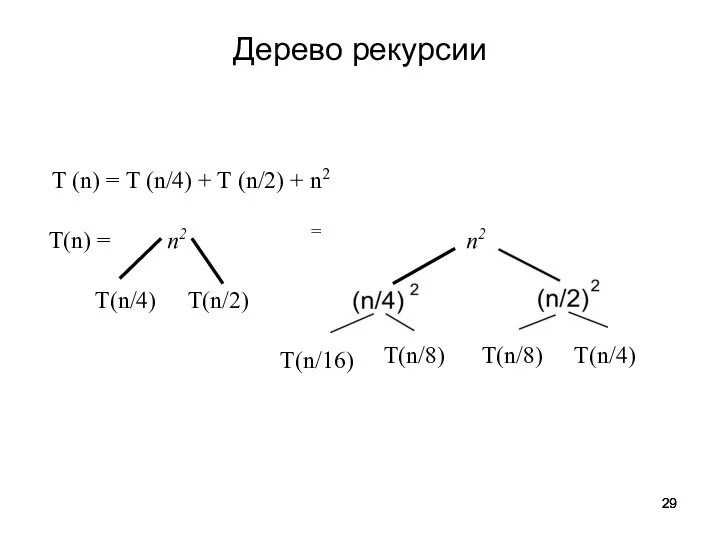
- 29. Дерево рекурсии
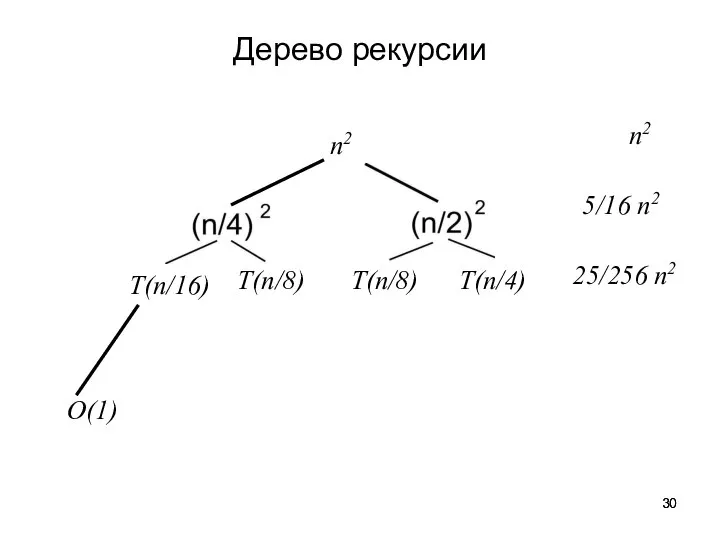
- 30. Дерево рекурсии
- 31. Сумма: по уровням (1 + 5/16 + 25/256 + . . . + 5k/16k + .
- 32. T (n) = aT (n/b) + f (n), a ≥ 1, b > 1, f (n)
- 33. 1. T (n) = 4T (n/2) + n a=4, b=2, f(n)=n При ε=1 выполняется условие для
- 34. 2. T (n) = 4T (n/2) + n2 a=4, b=2, f(n)=n2 второй случай теоремы T(n)=θ(n2*log n)
- 36. Скачать презентацию









![void mergeSort (int a[], int l, int r) { int mid; if](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1124721/slide-12.jpg)

![void mergeSort (int a[], int l, int r) { T(n) int mid;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1124721/slide-17.jpg)








 3D-проектирование в AutoCAD: создание 3D-модели объекта и её проекций
3D-проектирование в AutoCAD: создание 3D-модели объекта и её проекций Актуальность сайта Gdz
Актуальность сайта Gdz Кот и колбаса
Кот и колбаса Шифровки с новогодними письмами
Шифровки с новогодними письмами Табличные информационные модели моделирование и формализация
Табличные информационные модели моделирование и формализация Программное обеспечение для расчета стоимости грузоперевозок ООО НПЗ-Транс
Программное обеспечение для расчета стоимости грузоперевозок ООО НПЗ-Транс How to begin a programmer
How to begin a programmer PHP - Объектно-ориентированное программирование (2022) (4)
PHP - Объектно-ориентированное программирование (2022) (4) Электронная почта
Электронная почта Памятка клиенту. СББОЛ. Формирование сообщения в Банк
Памятка клиенту. СББОЛ. Формирование сообщения в Банк Цели информатизации образования
Цели информатизации образования Модификатор Edit Poly. Общие сведения. Полигональное моделирование
Модификатор Edit Poly. Общие сведения. Полигональное моделирование Программирование на Python. Алгоритмы и структуры данных. Часть 1. 10 занятие
Программирование на Python. Алгоритмы и структуры данных. Часть 1. 10 занятие Система поиска книг, фильмов и музыки
Система поиска книг, фильмов и музыки Программирование циклов
Программирование циклов Среда программирования Pascal ABC
Среда программирования Pascal ABC Технологические операторы, рассчитывающие паро-жидкостное равновесие в системе
Технологические операторы, рассчитывающие паро-жидкостное равновесие в системе Информационная система
Информационная система Тест: Паскаль. Вариант 3
Тест: Паскаль. Вариант 3 Презентация на тему Информация и информационные процессы
Презентация на тему Информация и информационные процессы  Элементы цифровой логики. Простейшие логическое схемы
Элементы цифровой логики. Простейшие логическое схемы Strides. Планомерное развитие Ваших проектов
Strides. Планомерное развитие Ваших проектов Локальные компьютерные сети (интерактивный плакат)
Локальные компьютерные сети (интерактивный плакат) Понятие и система средств массовой коммуникации
Понятие и система средств массовой коммуникации Windows 2000
Windows 2000 Что такое издательская система? Самостоятельная работа (вопросы)
Что такое издательская система? Самостоятельная работа (вопросы) Презентация1
Презентация1 Базы данных (БД)
Базы данных (БД)