Содержание
- 2. План Концепция криптосистемы с открытым ключом Элементы теории чисел Односторонние функции Алгоритм Диффи-Хелмана RSA Криптоалгоритмы на
- 3. 1 Концепция криптосистемы с открытым ключом Ключевой обмен, Электронно-цифровая подпись Аутентификация
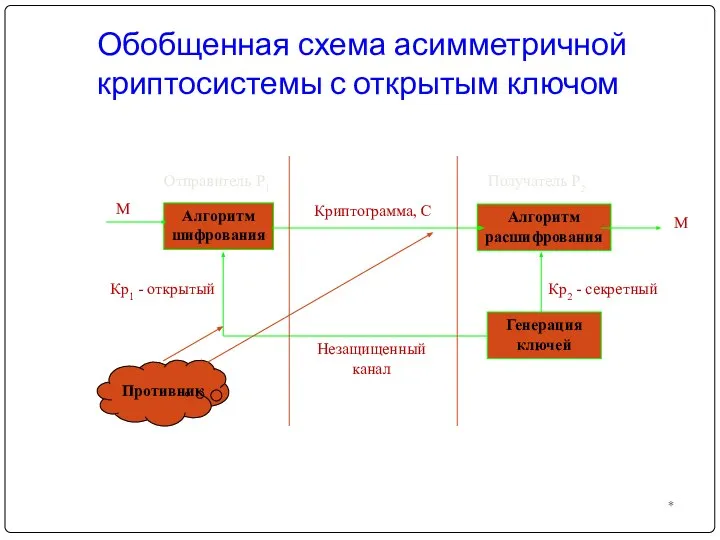
- 4. Обобщенная схема асимметричной криптосистемы с открытым ключом * Алгоритм шифрования Алгоритм расшифрования Генерация ключей Отправитель Р1
- 5. 2 Элементы теории чисел
- 12. 3 Односторонние (однонаправленные) функции Односторонние (однонаправленные) функции обладают следующим свойством: Если известно x , то вычислить
- 14. 4 Алгоритм Диффи-Хелмана
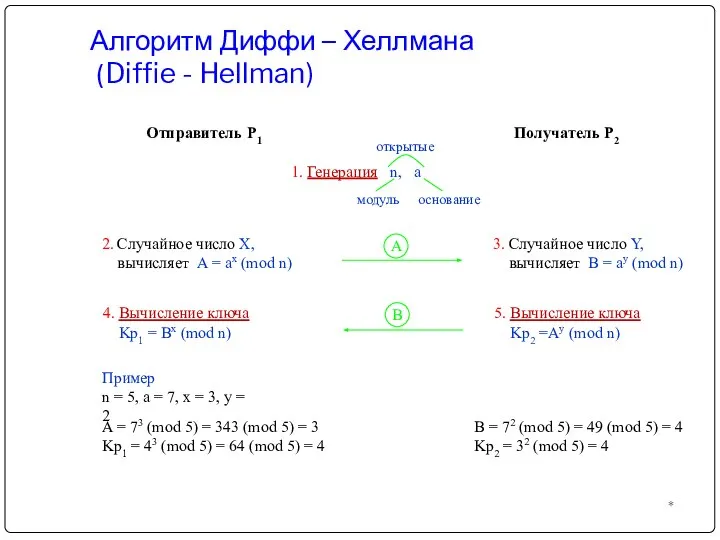
- 15. Алгоритм Диффи – Хеллмана (Diffie - Hellman) *
- 16. 5 RSA
- 17. АСИММЕТРИЧНЫЕ КРИПТОАЛГОРИТМЫ Алгоритм RSA
- 18. АСИММЕТРИЧНЫЕ КРИПТОАЛГОРИТМЫ
- 19. Алгоритм RSA (Rivest-Shamir-Adleman) * Генерация ключей Получатель 1. P, Q - простые, N = P ·
- 20. 6 КРИПТОАЛГОРИТМЫ НА ОСНОВЕ ЭЛЛИПТИЧЕСКИХ КРИВЫХ Общие положения Что такое Эллиптическая кривая? В общем случае эллиптическая
- 21. В случае криптографии с использованием эллиптических кривых приходится иметь дело с редуцированной формой эллиптической кривой, которая
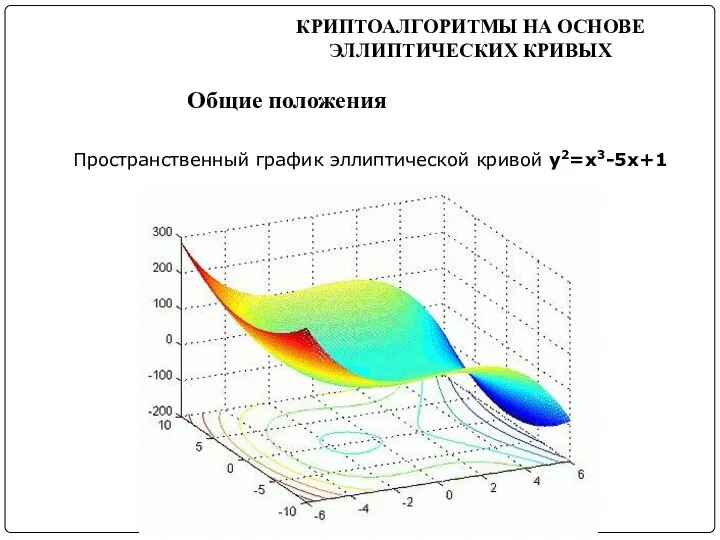
- 22. КРИПТОАЛГОРИТМЫ НА ОСНОВЕ ЭЛЛИПТИЧЕСКИХ КРИВЫХ Общие положения Пространственный график эллиптической кривой y2=x3-5x+1
- 23. Криптоалгоритм основан на “Проблеме Дискретного Логарифма Эллиптической Кривой” (Elliptic Curve Discrete Logarithm Problem – ECDLP): “Даны
- 24. КРИПТОАЛГОРИТМЫ НА ОСНОВЕ ЭЛЛИПТИЧЕСКИХ КРИВЫХ Общие положения Из-за трудности взлома алгоритм ECDLP можно применять для высоко
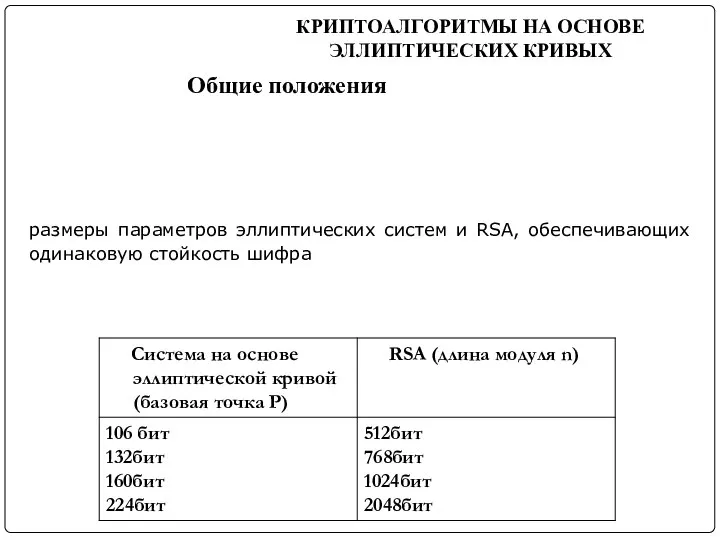
- 25. Использование эллиптических кривых позволяет строить высоко защищенные системы с ключами явно меньших размеров по сравнению с
- 26. КРИПТОАЛГОРИТМЫ НА ОСНОВЕ ЭЛЛИПТИЧЕСКИХ КРИВЫХ Некоторые проблемы и трудности в использовании систем на основе Эллиптической Кривой
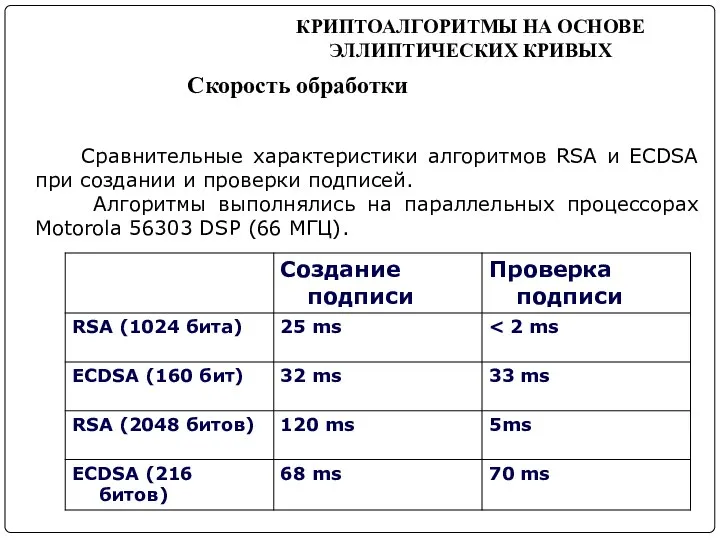
- 27. КРИПТОАЛГОРИТМЫ НА ОСНОВЕ ЭЛЛИПТИЧЕСКИХ КРИВЫХ Скорость обработки Сравнительные характеристики алгоритмов RSA и ECDSA при создании и
- 28. КРИПТОАЛГОРИТМЫ НА ОСНОВЕ ЭЛЛИПТИЧЕСКИХ КРИВЫХ Заключительные замечания Криптосистемы на основе эллиптической кривой получают все большее распространение
- 29. 7 Алгоритм Эль-Гамаля (El Gamal) * Генерация ключей 1. P, G - простые (P>G) 2. Х
- 30. ЭЦП RSA * Генерация ключей 1. P, Q - большие простые числа. 2. Модуль N =
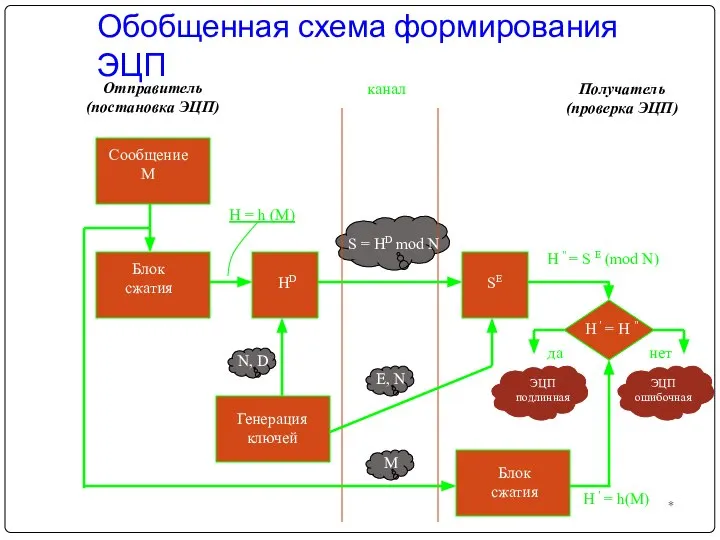
- 31. Обобщенная схема формирования ЭЦП * Отправитель (постановка ЭЦП) Получатель (проверка ЭЦП) Сообщение М Блок сжатия HD
- 33. Скачать презентацию
























 Оператор безусловного перехода GOTO
Оператор безусловного перехода GOTO Как перенести информацию из внешнего мира на какой-либо носитель
Как перенести информацию из внешнего мира на какой-либо носитель Ключевые слова
Ключевые слова Операционные системы
Операционные системы Социальные сети. You Tube
Социальные сети. You Tube Презентация на тему Основы Web-дизайна
Презентация на тему Основы Web-дизайна  Проектирование цифровых устройств
Проектирование цифровых устройств Отчет в рамках исполнения работ по государственному контракту на оказание услуг, выполнение работ
Отчет в рамках исполнения работ по государственному контракту на оказание услуг, выполнение работ Презентация на тему Программирование на языке Си
Презентация на тему Программирование на языке Си  IТ Образование для специалистов всех уровней!
IТ Образование для специалистов всех уровней! Технология установки, настройки и обновления прикладного программного обеспечения
Технология установки, настройки и обновления прикладного программного обеспечения Форматирование текста по образцу в Microsoft Word. Урок 10
Форматирование текста по образцу в Microsoft Word. Урок 10 Продажа металлолома и сырых шкур
Продажа металлолома и сырых шкур Основы музейных коммуникаций
Основы музейных коммуникаций Зертханалық жұмыс
Зертханалық жұмыс Зажигаем свечу. Создание анимации в программе Fdobe Photoshop
Зажигаем свечу. Создание анимации в программе Fdobe Photoshop Автоматизация документооборота
Автоматизация документооборота Знаки и знаковые системы
Знаки и знаковые системы Массивы. Двумерные массивы. Спиралевидный и змеевидный обходы
Массивы. Двумерные массивы. Спиралевидный и змеевидный обходы Создание таблицы
Создание таблицы BlockChain
BlockChain ООП на Delphi
ООП на Delphi Тренинг для операторов
Тренинг для операторов Отчет о деятельности Пресс-центра ППОС СФУ за 2018 год
Отчет о деятельности Пресс-центра ППОС СФУ за 2018 год Интернет - мошенничество
Интернет - мошенничество CryptoBox. Применение шифрования
CryptoBox. Применение шифрования Алгоритмы. Алгоритмизация юридической деятельности
Алгоритмы. Алгоритмизация юридической деятельности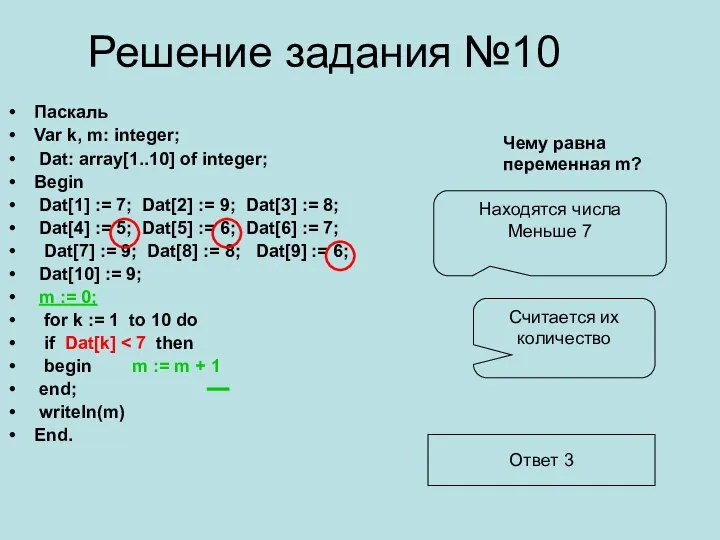 Решение задания №10. Паскаль
Решение задания №10. Паскаль