Содержание
- 2. АВЛ-деревья Возможное промежуточное решение - ввести менее строгий критерий сбалансированности. Определение предложено в 1962 году Г.М.
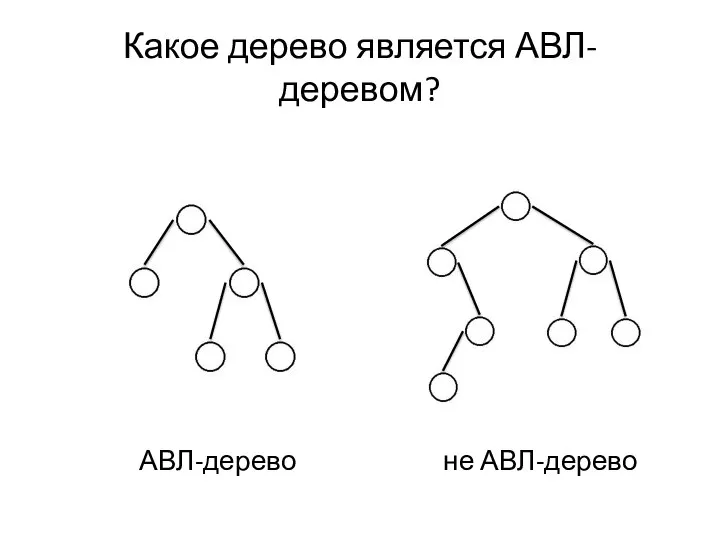
- 3. Определение. Дерево поиска называется АВЛ-деревом, если для каждой его вершины высоты левого и правого поддеревьев отличается
- 4. АВЛ-дерево не АВЛ-дерево Какое дерево является АВЛ-деревом?
- 5. «Плохие» АВЛ-деревья Адельсон-Вельский и Ландис доказали теорему которая, гарантирует, что АВЛ-дерево никогда не будет по высоте
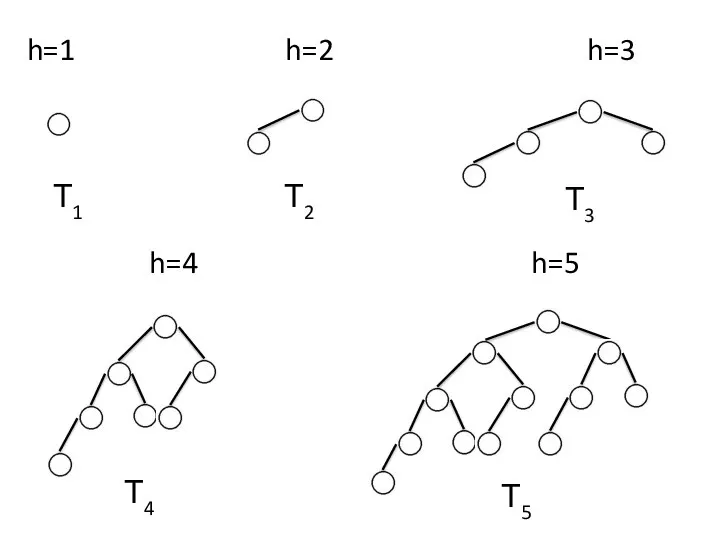
- 6. Определение. «Плохим» будем называть АВЛ-дерево, которое имеет наименьшее чисто вершин при фиксированной высоте. Какова структура «плохого»
- 7. h=1 h=2 h=3 h=4 h=5 Т1 Т2 Т3 Т5 Т4
- 8. Заметим, что Т3 = Т2+Т1 +1; Т4 = Т2+Т3 +1; Т5 = Т3+Т4+1. Для построения Тh
- 9. Построение АВЛ-дерева Рассмотрим, что может произойти при включении в сбалансированное по высоте дерево новой вершины. Пусть
- 10. Пусть добавляется вершина в правое поддерево. Возможны три случая: Если hL > hR , то hL
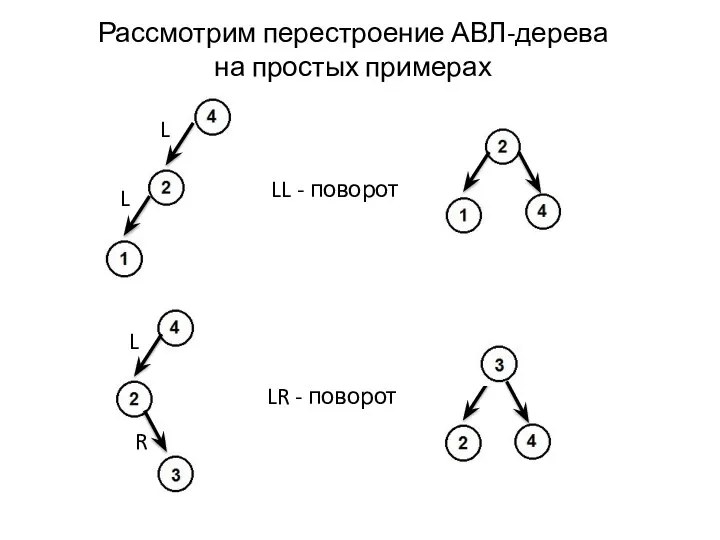
- 11. Рассмотрим перестроение АВЛ-дерева на простых примерах LL - поворот LR - поворот
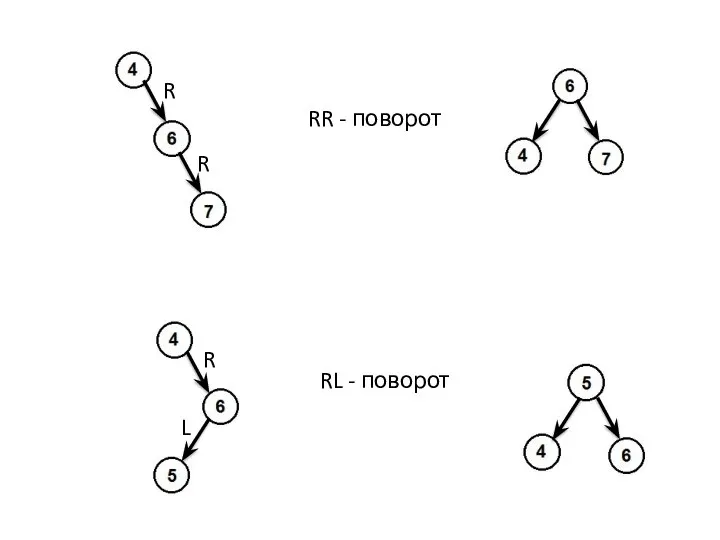
- 12. RR - поворот RL - поворот
- 13. Идея алгоритма построения АВЛ-дерева Вначале добавим новую вершину в дерево так же как в случайное, т.е.
- 14. Задачи при перестроении АВЛ-дерева
- 15. При включении новой вершины её баланс равен нулю. При движении назад по пути поиска показатель баланса
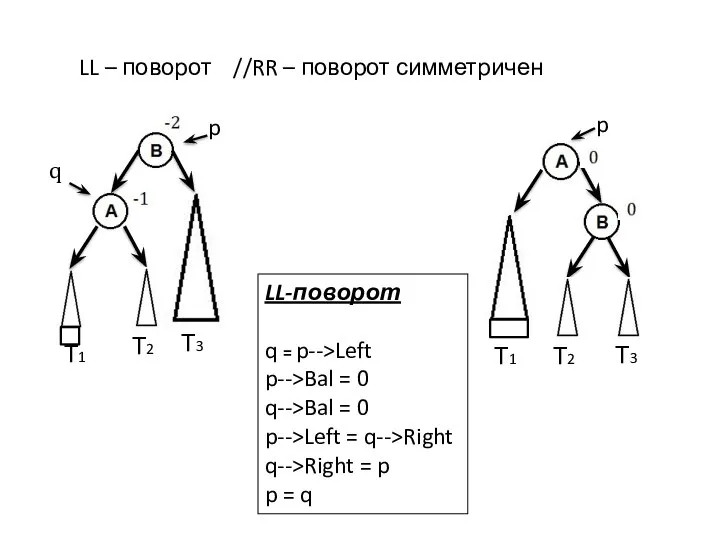
- 16. LL – поворот //RR – поворот симметричен Т1 Т2 Т3 Т1 Т2 Т3 p q p
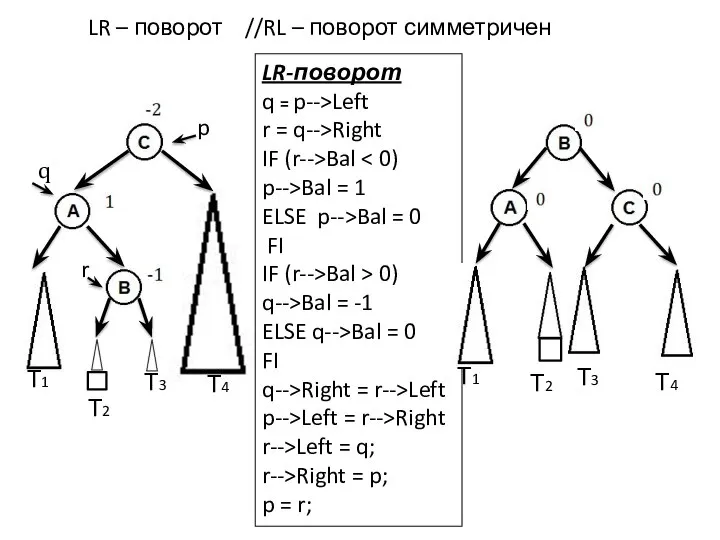
- 17. LR – поворот //RL – поворот симметричен Т1 Т2 Т3 p q LR-поворот q = p-->Left
- 18. Введем логическую переменную Rost которая будет показывать, что дерево увеличилось ( Rost =да) Добавить АВЛ (
- 19. ELSE IF (p-->Data Right) IF (Rost = да) IF (p-->Bal Bal = 0; Rost = нет
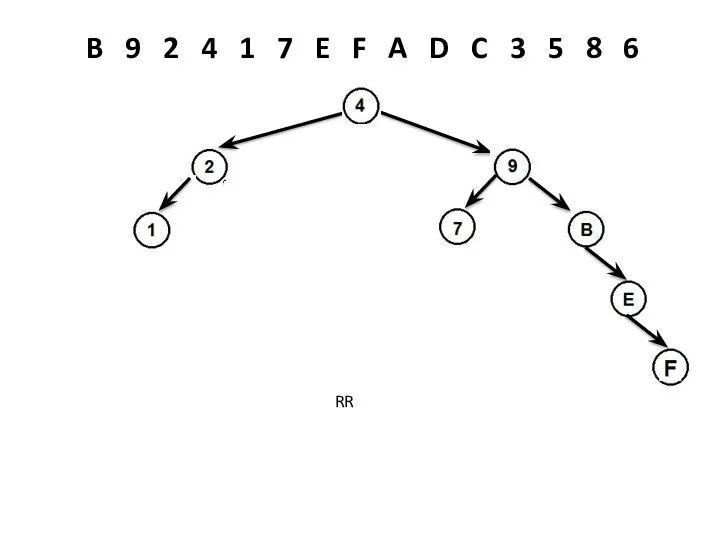
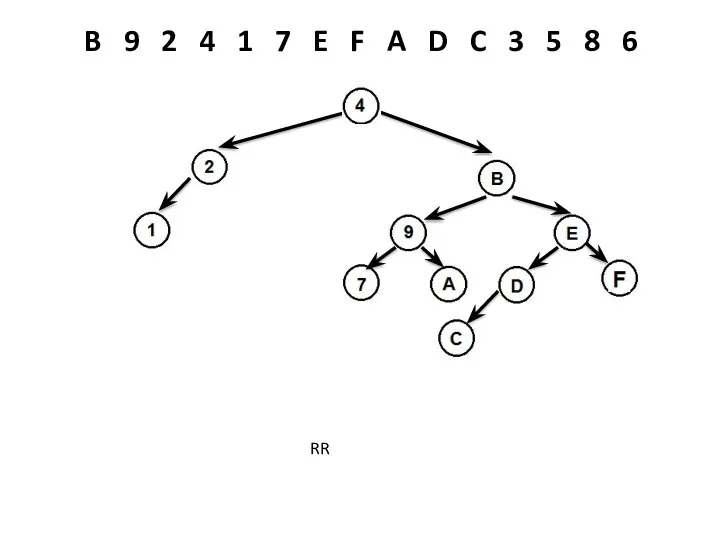
- 20. B 9 2 4 1 7 E F A D C 3 5 8 6 LL
- 21. B 9 2 4 1 7 E F A D C 3 5 8 6 RL
- 23. Скачать презентацию












 Компьютерная графика
Компьютерная графика Алгоритмизация и программирование С#. (Лекция 1.1)
Алгоритмизация и программирование С#. (Лекция 1.1)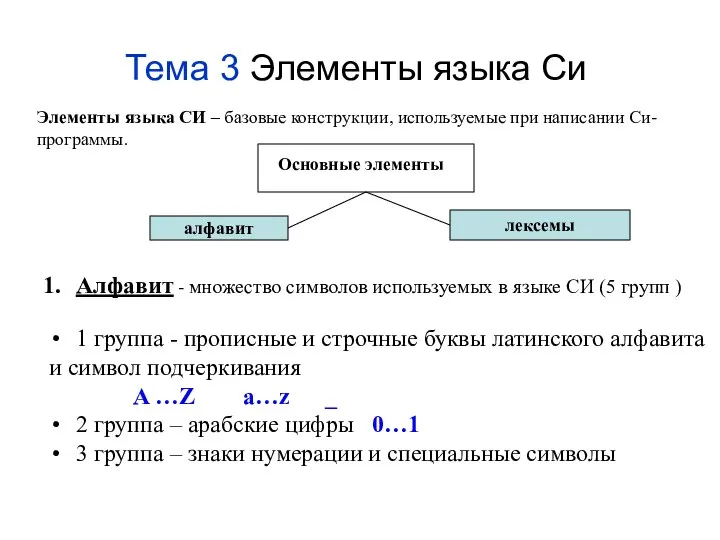 Элементы языка Си
Элементы языка Си Отрисовка дизайна сайта
Отрисовка дизайна сайта Безопасность в сети для 2-4 классов
Безопасность в сети для 2-4 классов Человек на пути
Человек на пути Лекция 1-4 (Топологии_Методы доступа_Архитектура)
Лекция 1-4 (Топологии_Методы доступа_Архитектура) Тестовая документация
Тестовая документация Internet Protocol (IP)
Internet Protocol (IP) Использование веб-сервисов
Использование веб-сервисов Формы представления информации
Формы представления информации Структуры и алгоритмы обработки данных. Лекция 1
Структуры и алгоритмы обработки данных. Лекция 1 Основные свойства информационных банков СПС
Основные свойства информационных банков СПС Создание Flash-анимации
Создание Flash-анимации Защищенные операционные системы
Защищенные операционные системы Представление информации в форме таблиц
Представление информации в форме таблиц Изучение языков программирования
Изучение языков программирования Мобильное приложение. Поиск или нахождение потерянной вещи
Мобильное приложение. Поиск или нахождение потерянной вещи Информация, информационные процессы и информационное общество
Информация, информационные процессы и информационное общество Модификация данных
Модификация данных Компьютерная игра Death Patrol
Компьютерная игра Death Patrol Управление персоналом. Правила подготовки докладов в Power Point
Управление персоналом. Правила подготовки докладов в Power Point Деревья. Лекция 6
Деревья. Лекция 6 Дискретные модели данных в компьютере
Дискретные модели данных в компьютере Лекция 5_ОАИП_2020
Лекция 5_ОАИП_2020 Новые ИТ за 15 лет
Новые ИТ за 15 лет Информационные ресурсы и сервисы Интернета
Информационные ресурсы и сервисы Интернета Методика построения А3. Дивизион Сталь Дирекция по операционным улучшения
Методика построения А3. Дивизион Сталь Дирекция по операционным улучшения