Элементы комбинаторики, теории множеств и математической логики. Операции импликация, эквиваленция

Логическая функция — это однозначное соответствие каждой из возможных комбинаций значений логических переменных одной из логических констант.
Логическую переменную логической функции называют логическим аргументом, который может принимать только одно из двух возможных значений: 0 и 1
Способом описания логической функции является таблица истинности, которая позволяет для каждого набора логических аргументов описать единственное значение логической функции.
Основные операции над аргументами: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция.

Отрицанием называется высказывание <не А>, обозначаемое A, которое считается истинным, если А ложно, и ложным, если А истинно.

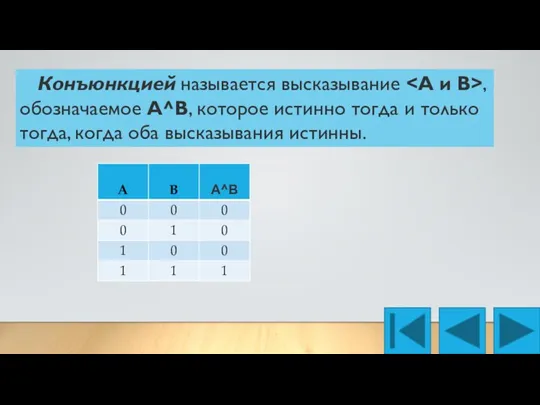
Конъюнкцией называется высказывание <А и В>, обозначаемое А^В, которое истинно тогда и только тогда, когда оба высказывания истинны.

Дизъюнкцией называется высказывание<А или В>, обозначаемое АvВ, которое считается ложным тогда и только тогда, когда оба высказывания ложны.

Импликацией называется высказывание <если А, то В>, обозначается А→В, которое считается ложным тогда и только тогда, когда высказывание А истинно, а высказывание В ложно.

Пример 1.
Рассмотрим высказывания:
Число 3 делится на 2 (A1);
Число 4 является простым (A2);
Число 5 больше 1 (A3).
A1=0, A2=0, A3=1
Построим высказывания A1→A2, A3→A1 и A2→A3:
1) Если три делится на два, то четыре — простое число (A1→A2);
2) Если пять больше единицы, то три делится на два (A3→A1);
3) Если четыре — простое число, то пять больше единицы (A2→A3).
A1→A2=0→0=1
A3→A1=1→0=0
A2→A3=0→1=1

Пример 2.
Запишем обратные и противоположные импликации для высказываний A1→A2, A3→A1 и A2→A3 из предыдущего примера.
1) Если четыре является простым числом, то три делится на два (A2→A1); A2→A1=0→0=1
2) Если три делится на два, то пять больше единицы (A1→A3); A1→A3=0→1=1
3) Если пять больше единицы, то четыре является простым числом (A3→A2). A3→A2=1→0=0
Переходим к противоположным импликациям:
1) Если три не делится на два, то четыре не является простым числом (A1'→A2');
2) Если пять не больше единицы, то три не делится на два (A3'→A1');
3) Если четыре не является простым числом, то пять не больше единицы (A2'→A3').
Так как
A1=A2=0, A3=1,
то
A1=A2=1, A3=0.
Следовательно,
A1→A2=A3→A1=1, A2→A3=0.

Эквиваленцией называется высказывание <для А необходимо и достаточно В>, обозначается А↔В, которое истинно тогда и только тогда, когда оба высказывания А и В одновременно либо истинны, либо ложны.

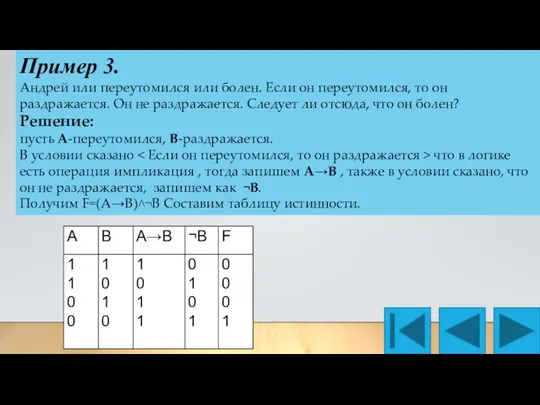
Пример 3.
Андрей или переутомился или болен. Если он переутомился, то он раздражается. Он не раздражается. Следует ли отсюда, что он болен?
Решение:
пусть А-переутомился, В-раздражается.
В условии сказано < Если он переутомился, то он раздражается > что в логике есть операция импликация , тогда запишем А→В , также в условии сказано, что он не раздражается, запишем как ¬В.
Получим F=(А→В)˄¬В Составим таблицу истинности.

Основные законы алгебры логики
1. Закон тождества
Всякое высказывание тождественно самому себе.
A = A
2. Закон исключенного третьего
Высказывание может быть либо истинным, либо ложным, третьего не дано. Следовательно, результат логического сложения высказывания и его отрицания всегда принимает значение «истина».
АvA=1

Основные законы алгебры логики
3. Закон непротиворечия
Высказывание не может быть одновременно истинным и ложным. Если высказывание A истинно, то его отрицание НЕ A должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно.
А^A=0

Основные законы алгебры логики
Закон двойного отрицания
Если дважды отрицать некоторое высказывание, то в результате получим исходное высказывание.
A=A
5. Переместительный (коммутативный) закон
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
А^В=B^A

Основные законы алгебры логики
6. Сочетательный (ассоциативный) закон
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
Аv(ВvС)= (АvВ)vС
(А^В)^С= А^(В ^С)
7. Распределительный (дистрибутивный) закон
Определяет правило выноса общего высказывания за скобку.
Аv(В^С)= (А^В)v(А^С)
Аv(В^С)= (АvВ)^(АvС)

Основные законы алгебры логики
8. Закон общей инверсии Закон де Моргана
(А^В)=AvB (АvВ)=A^B
9. Закон равносильности (идемпотентности)
AvA= A
10.Законы исключения констант
Av0=A Av1=1 A^1=A A^0=0

Основные законы алгебры логики
11. Закон поглощения
Вv(А^В)=В
A^(АvВ)=A
12. Закон исключения (склеивания)
(А^В)v(А^В)=B
(АvВ)^(АvВ)=B
Законы алгебры логики применяются в следующей последовательности:
1)Правило де Моргана
2)Сочетательный закон
3)Правило операций переменной с её инверсией
4)Правило операций с константами

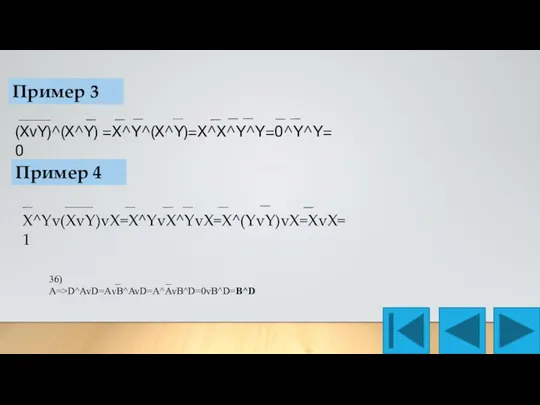
Пример 3
(XvY)^(X^Y) =X^Y^(X^Y)=X^X^Y^Y=0^Y^Y=0
Пример 4
X^Yv(XvY)vX=X^YvX^YvX=X^(YvY)vX=XvX=1
36) _ _
A=>D^AvD=АvB^AvD=A^AvB^D=0vB^D=B^D

Замена операции импликации
Заменить операцию импликации можно в соответствии со следующим правилом: