Графы. Часть 5

Рассматриваемые алгоритмы
Алгоритм Дейкстры
Находит кратчайшее расстояние от заданной вершины до всех остальных, базируется на обходе в ширину.
Асимптотика O(M log(N)).
Алгоритм Флойда-Уоршелла
Находит кратчайшее расстояние между всеми парами вершин.
Асимптотика O(N3).

Приоритетная очередь (std::priority_queue)
Требуется подключение библиотеки #include
По умолчанию первый объект в очереди – самый наибольший.
Объявление объекта приоритетной очереди
priority_queue<‘тип данных’> que;
или
priority_queue<‘тип данных’, ’тип контейнера’<‘тип данных’>,
‘тип компаратора’<‘тип данных’ >> que;
По умолчанию ‘тип контейнера’ – std::vector, а ‘тип компаратора’ – std::less.
Добавление объекта в очередь que.push(obj);
Получение первого объекта из очереди que.top();
Удаление первого элемента из очереди que.pop();
Проверка, пустая ли очередь que.empty();

Алгоритм Дейкстры
Для каждой вершины будем хранить расстояние до неё. Изначально расстояние до всех вершин равно INF (очень большая константа), а до стартовой – 0.
В каждой вершине помимо списка смежных с ней вершин будем хранить и длину ребра, которым они соединены.
Во время обхода будем использовать не обычную, а приоритетную очередь. Хранить в ней будем пары чисел <‘расстояние до вершины’,’номер вершины’>.
Положим в очередь пару <0, ‘стартовая вершина’>, следующие пункты будем повторять, пока очередь не опустеет.
Вынем из очереди верхнюю пару. Если расстояние в этой паре не больше, чем текущее в вершине из этой пары, то перейдём к следующему шагу. Иначе – повторим текущий.
Переберём все смежные вершины. Если расстояние до текущей вершины + длина ребра до смежной меньше текущего расстояния в смежной вершине, то обновим в ней расстояние и добавим в очередь пару <‘новое расстояние до смежной вершины’,’номер смежной вершины’>. Если для решения задачи нужно будет знать путь, то на этом шаге нужно запомнить, что предком смежной вершины является текущая.

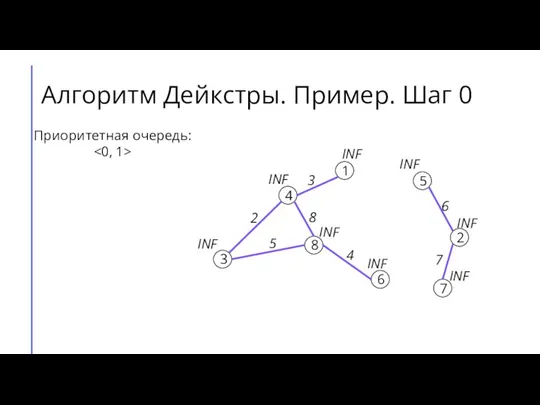
Алгоритм Дейкстры. Пример. Шаг 0
7
2
6
5
8
3
4
1
3
4
8
5
2
6
7
INF
INF
INF
INF
INF
INF
INF
INF
Приоритетная очередь:
<0, 1>

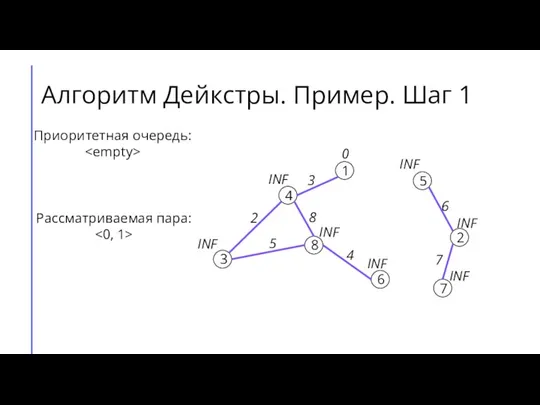
Алгоритм Дейкстры. Пример. Шаг 1
7
2
6
5
8
3
4
1
3
4
8
5
2
6
7
0
INF
INF
INF
INF
INF
INF
INF
Приоритетная очередь:
Рассматриваемая пара:
<0, 1>

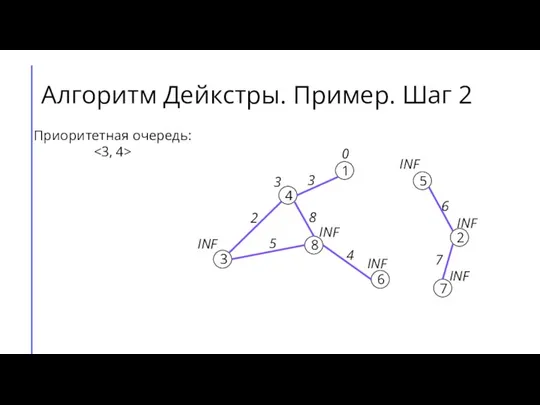
Алгоритм Дейкстры. Пример. Шаг 2
7
2
6
5
8
3
4
1
3
4
8
5
2
6
7
0
3
INF
INF
INF
INF
INF
INF
Приоритетная очередь:
<3, 4>

Алгоритм Дейкстры. Пример. Шаг 3
7
2
6
5
8
3
4
1
3
4
8
5
2
6
7
0
3
INF
INF
INF
INF
INF
INF
Приоритетная очередь:
Рассматриваемая пара:
<3, 4>

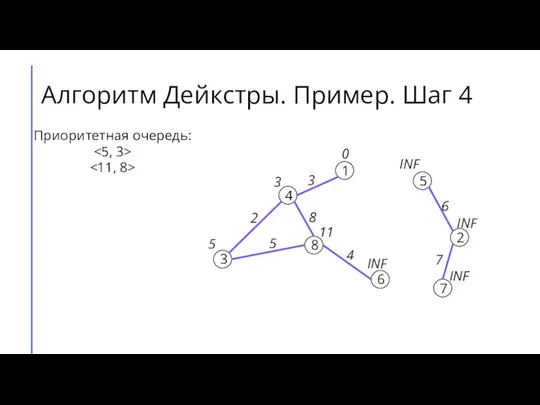
Алгоритм Дейкстры. Пример. Шаг 4
7
2
6
5
8
3
4
1
3
4
8
5
2
6
7
0
3
5
INF
11
INF
INF
INF
Приоритетная очередь:
<5, 3>
<11, 8>

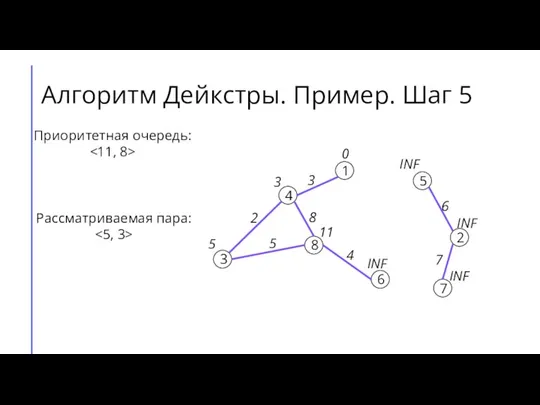
Алгоритм Дейкстры. Пример. Шаг 5
7
2
6
5
8
3
4
1
3
4
8
5
2
6
7
0
3
5
INF
11
INF
INF
INF
Приоритетная очередь:
<11, 8>
Рассматриваемая пара:
<5, 3>

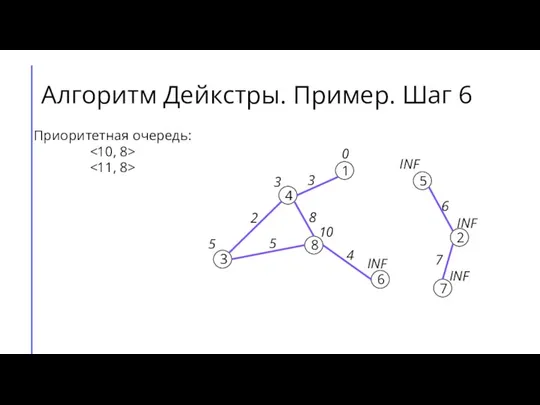
Алгоритм Дейкстры. Пример. Шаг 6
7
2
6
5
8
3
4
1
3
4
8
5
2
6
7
0
3
5
INF
10
INF
INF
INF
Приоритетная очередь:
<10, 8>
<11, 8>

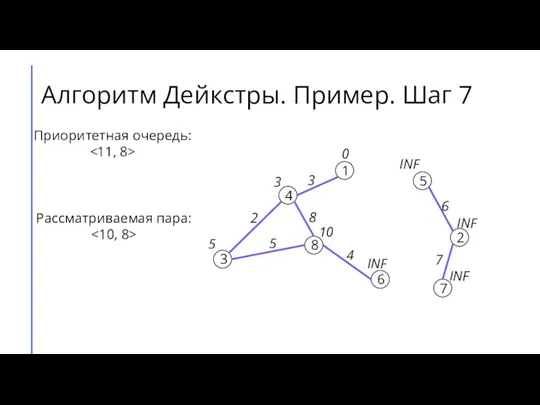
Алгоритм Дейкстры. Пример. Шаг 7
7
2
6
5
8
3
4
1
3
4
8
5
2
6
7
0
3
5
INF
10
INF
INF
INF
Приоритетная очередь:
<11, 8>
Рассматриваемая пара:
<10, 8>

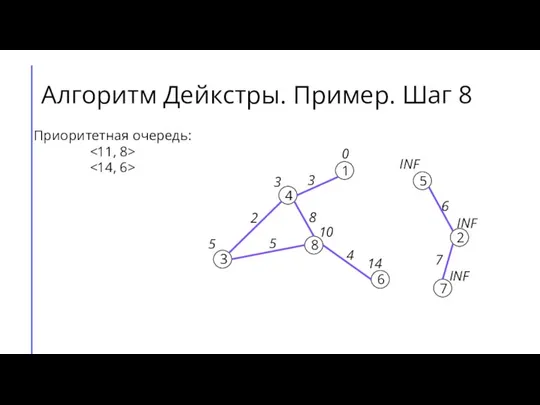
Алгоритм Дейкстры. Пример. Шаг 8
7
2
6
5
8
3
4
1
3
4
8
5
2
6
7
0
3
5
14
10
INF
INF
INF
Приоритетная очередь:
<11, 8>
<14, 6>

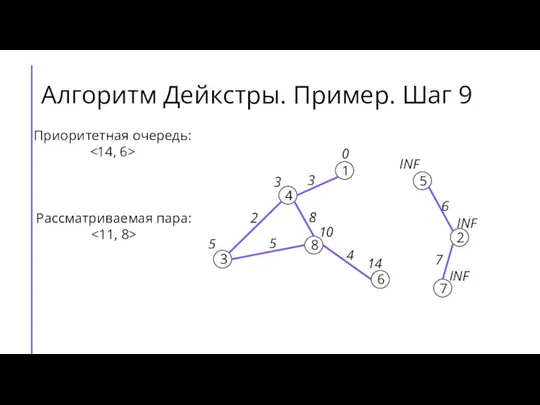
Алгоритм Дейкстры. Пример. Шаг 9
7
2
6
5
8
3
4
1
3
4
8
5
2
6
7
0
3
5
14
10
INF
INF
INF
Приоритетная очередь:
<14, 6>
Рассматриваемая пара:
<11, 8>

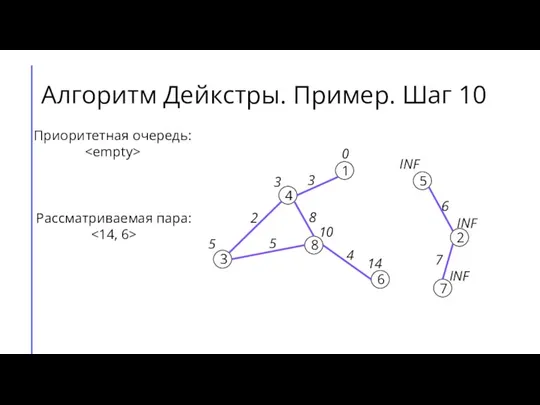
Алгоритм Дейкстры. Пример. Шаг 10
7
2
6
5
8
3
4
1
3
4
8
5
2
6
7
0
3
5
14
10
INF
INF
INF
Приоритетная очередь:
Рассматриваемая пара:
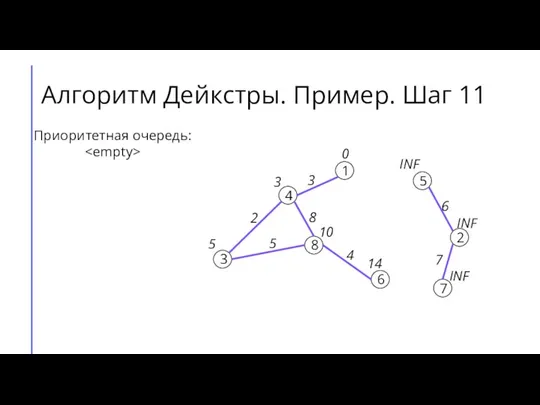
<14, 6>

Алгоритм Дейкстры. Пример. Шаг 11
7
2
6
5
8
3
4
1
3
4
8
5
2
6
7
0
3
5
14
10
INF
INF
INF
Приоритетная очередь:

Задача
Пусть дан ненаправленный взвешенный граф из N вершин и M рёбер. Рёбра описываются числами U, V и D, которые означают, что между вершинами с номерами U и V есть ребро длиной D. Далее даны два числа S и F – номера вершин, между которыми нужно найти кратчайший путь.
Решение
Напишем алгоритм Дейкстры с запоминанием предка. Запустим алгоритм из вершины S, после чего восстановим путь перемещаясь по предкам из вершины F.

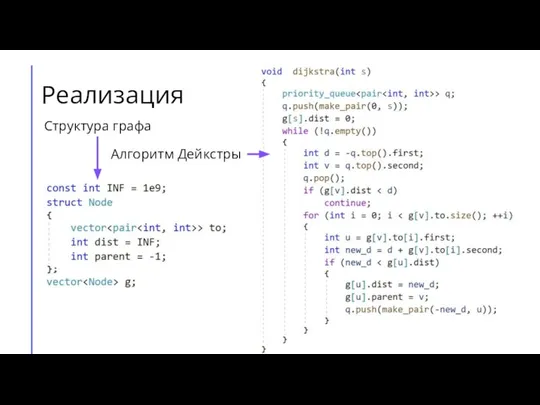
Реализация
Структура графа
Алгоритм Дейкстры

Реализация
Восстановление пути
Ввод графа и запуск алгоритма

Алгоритм Флойда-Уоршелла
Будем хранить матрицу расстояний между всеми парами вершин d[N][N].
Если в графе есть ребро из вершины i в вершину j длиной L, то d[i][j] = L. Расстояние от любой вершины до самой себя равно 0, т.е. d[i][j] = 0,
если i = j. Для всех остальных пар i и j d[i][j] = INF.
Алгоритм состоит из N фаз. Перед k-ой фазой в d[i][j] хранится минимальный путь, проходящий через вершины с номерами, меньшими k, или INF, если пути между данными вершинами не найдено.
Во время k-ой фазы путь между вершинами i и j может либо сохраниться, либо пройти через вершину c номером k, если суммарный путь от вершины i в вершину k и из вершины k в вершину j меньше, чем d[i][j].
То есть на k-ой фазе d[i][j] = min(d[i][j], d[i][k] + d[k][j]).
Алгоритм работает как с ориентированными так и с неориентированными графами. Алгоритм не работает, если в графе есть циклы с отрицательным весом.

Реализация
Пусть дан взвешенный ориентированный граф из N вершин и M рёбер. Требуется найти кратчайшее расстояние между всеми парами вершин. Веса рёбер положительны.

Восстановление пути в алгоритме Флойда-Уоршелла
Заведём дополнительную матрицу p[N][N], заполненную -1.
Когда расстояние между вершинами i и j обновляется благодаря проходу через вершину k запомним это (p[i][j] = k).
Если d[i][j] = INF, то пути не существует, а значит восстанавливать нечего.
Теперь мы знаем, что если путь существует p[i][j] = -1, то кратчайший путь между этими вершинами – непосредственный переход из i в j. Иначе следует восстановить пути из i в p[i][j] и из p[i][j] в j, объединение которых и будет восстановленным путём
из i в j.
Восстановление удобно реализуется рекурсивной функцией.