Слайд 2Определение
Граф – это набор вершин, некоторые пары из которых соединены между собой

рёбрами.
Связный граф – это граф, из любой вершины которого по рёбрам можно попасть в любую другую.
Направленный граф – это граф, по рёбрам которого можно передвигаться только в одном заданном направлении.
Ациклический граф – это граф, не содержащий циклов.
Дерево – это связный граф, имеющий N вершин и N-1 ребро.
Взвешенный граф – это граф, в котором каждое ребро имеет свой вес (обычно длину).
Компонента связности – максимальный по включению связный подграф.
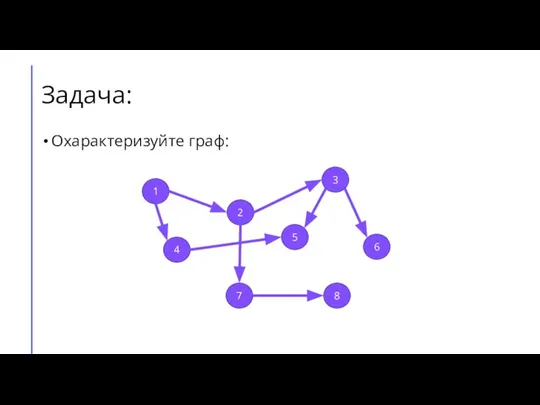
Слайд 3Задача:
Охарактеризуйте граф:
1
2
3
4
5
6
7
8
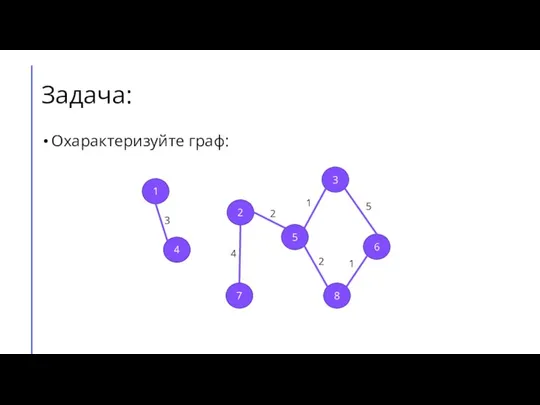
Слайд 4Задача:
Охарактеризуйте граф:
1
2
3
4
5
6
7
8
3
2
4
1
5
2
1
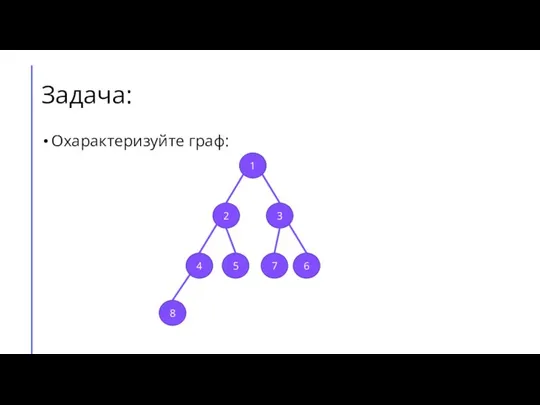
Слайд 5Задача:
Охарактеризуйте граф:
1
2
3
4
5
6
8
7
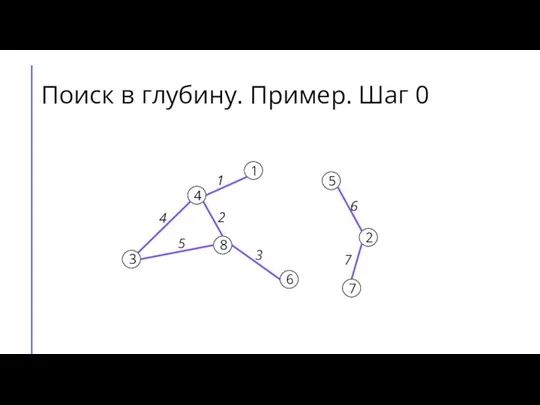
Слайд 6Поиск (обход) в глубину (DFS)
Для каждой вершины графа будем хранить её цвет.

Пусть изначально вершины будут белыми, когда мы в них входим, они будут становиться серыми, а когда выходим – чёрными.
Будем перебирать вершины графа. Если встречаем белую вершину – запускаем из неё поиск в глубину.
Во время поиска в глубину перебираем все вершины, смежные той, в которой сейчас находится алгоритм, и по очереди запускаем из них поиск в глубину.
Если поиск запущен не из белой вершины, то дальше его продолжать не следует.
Слайд 7Поиск в глубину. Пример. Шаг 0
7
2
6
5
8
3
4
1
1
3
2
5
4
6
7
Слайд 8Поиск в глубину. Пример. Шаг 1
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
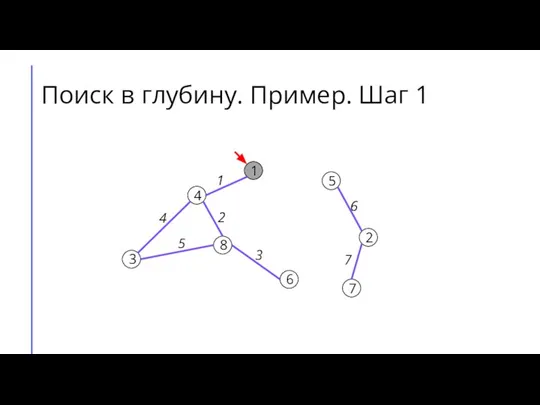
Слайд 9Поиск в глубину. Пример. Шаг 2
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
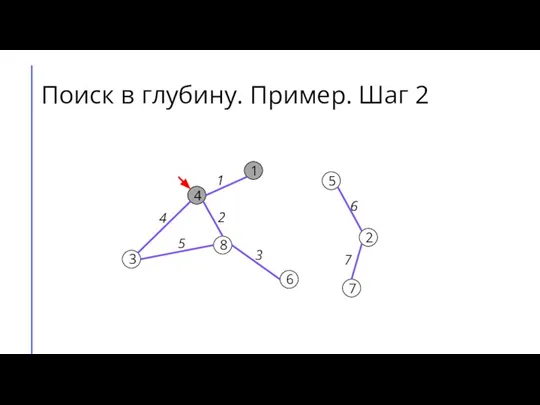
Слайд 10Поиск в глубину. Пример. Шаг 3
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
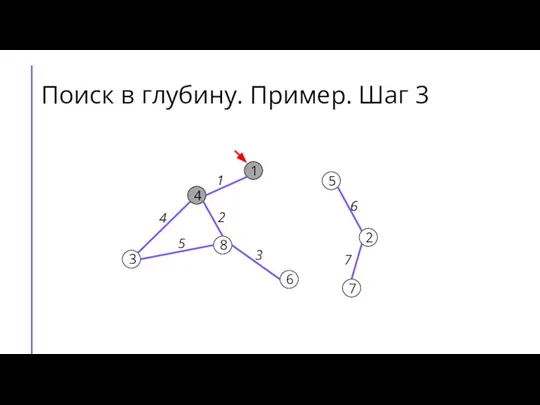
Слайд 11Поиск в глубину. Пример. Шаг 4
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
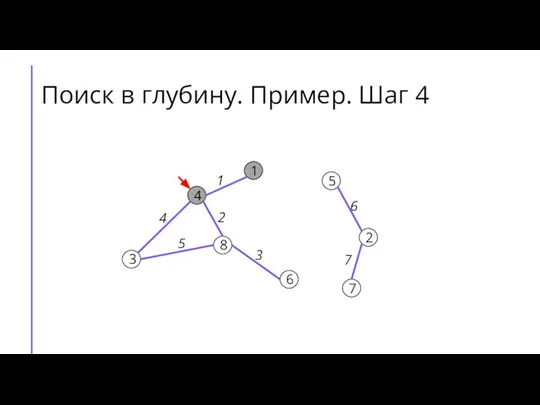
Слайд 12Поиск в глубину. Пример. Шаг 5
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
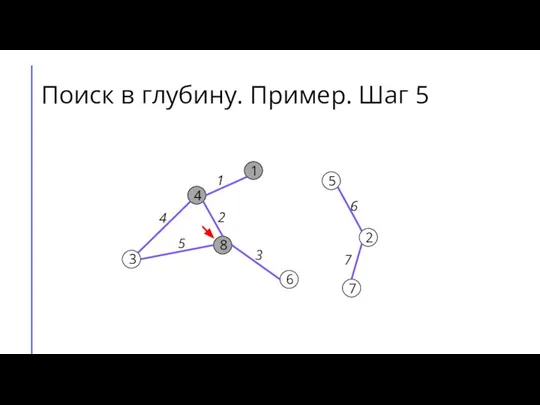
Слайд 13Поиск в глубину. Пример. Шаг 6
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
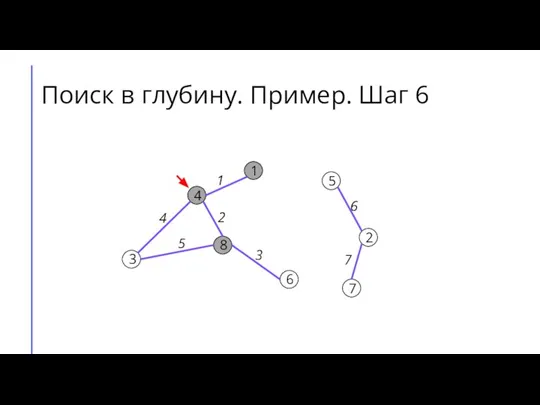
Слайд 14Поиск в глубину. Пример. Шаг 7
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
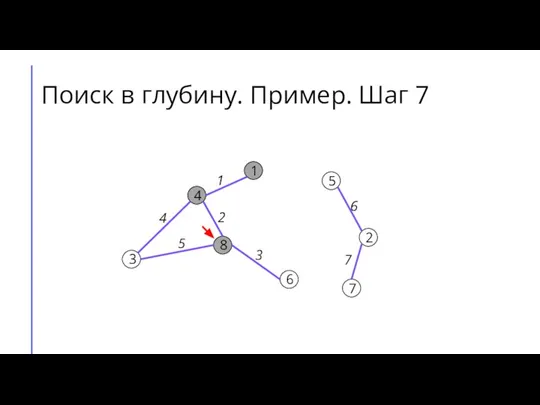
Слайд 15Поиск в глубину. Пример. Шаг 8
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
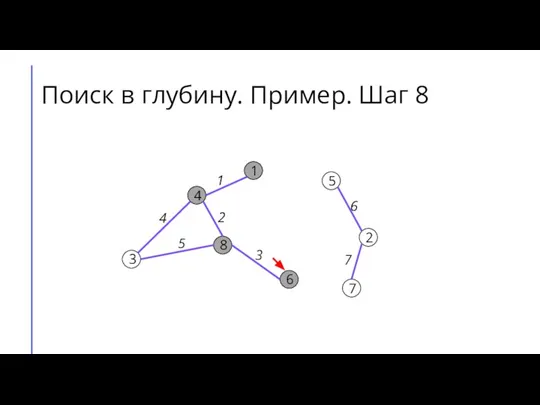
Слайд 16Поиск в глубину. Пример. Шаг 9
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
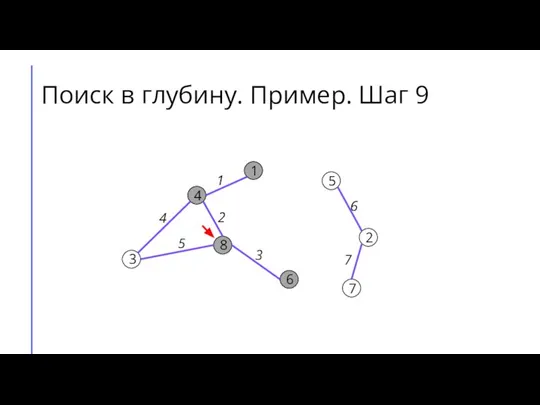
Слайд 17Поиск в глубину. Пример. Шаг 10
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
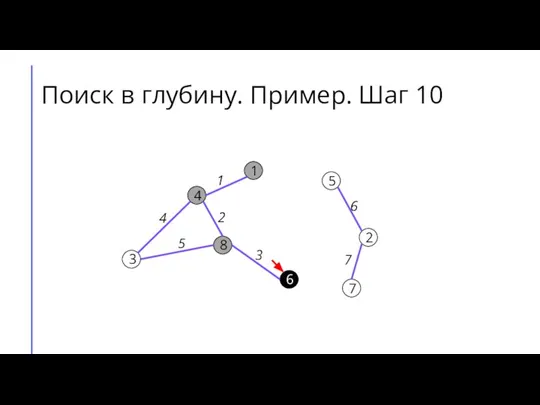
Слайд 18Поиск в глубину. Пример. Шаг 11
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
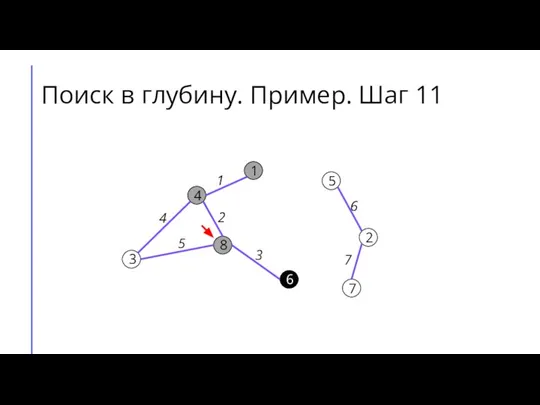
Слайд 19Поиск в глубину. Пример. Шаг 12
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
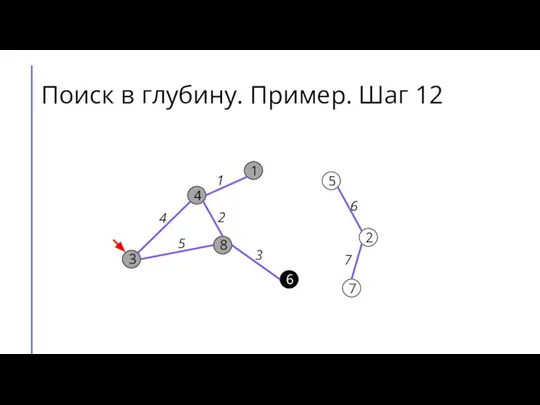
Слайд 20Поиск в глубину. Пример. Шаг 13
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Слайд 21Поиск в глубину. Пример. Шаг 14
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Слайд 22Поиск в глубину. Пример. Шаг 15
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Слайд 23Поиск в глубину. Пример. Шаг 16
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Слайд 24Поиск в глубину. Пример. Шаг 17
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
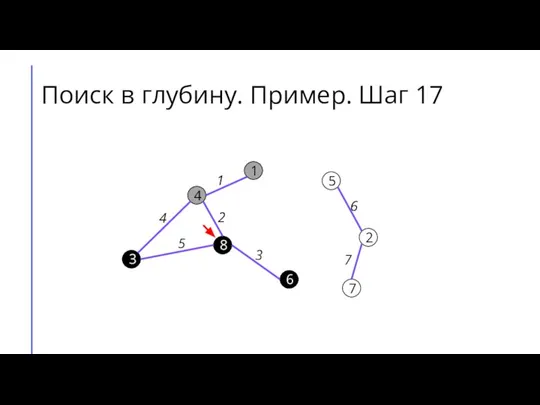
Слайд 25Поиск в глубину. Пример. Шаг 18
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
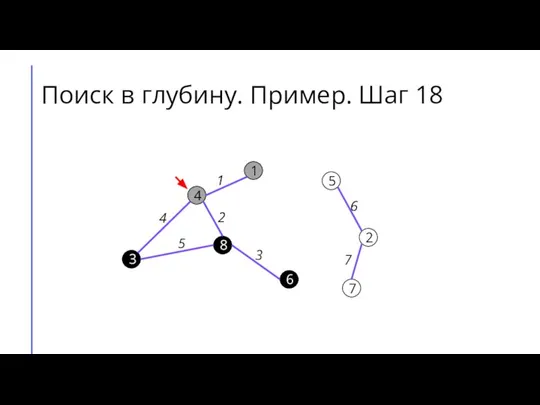
Слайд 26Поиск в глубину. Пример. Шаг 19
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
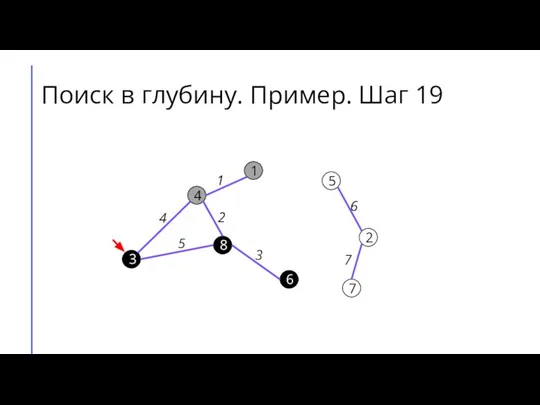
Слайд 27Поиск в глубину. Пример. Шаг 20
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
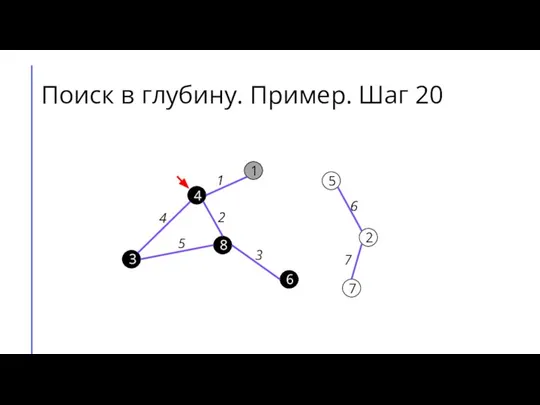
Слайд 28Поиск в глубину. Пример. Шаг 21
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
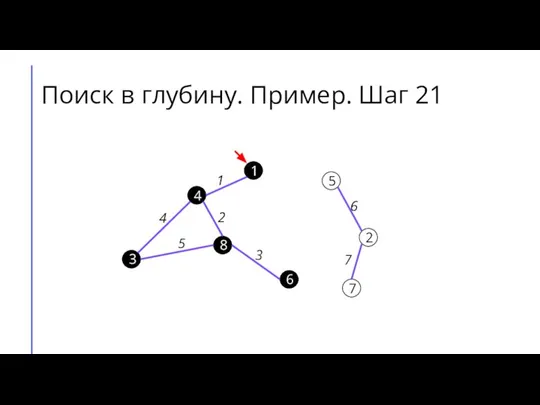
Слайд 29Поиск в глубину. Пример. Шаг 22
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
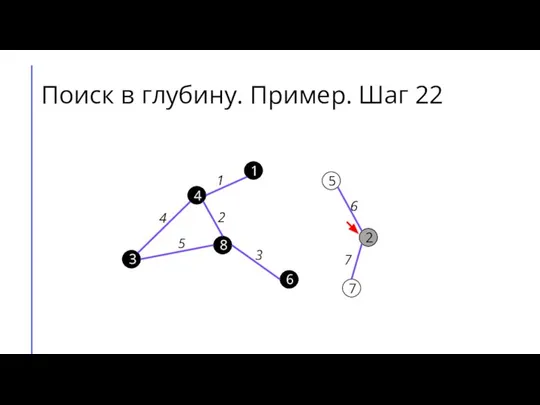
Слайд 30Поиск в глубину. Пример. Шаг 23
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
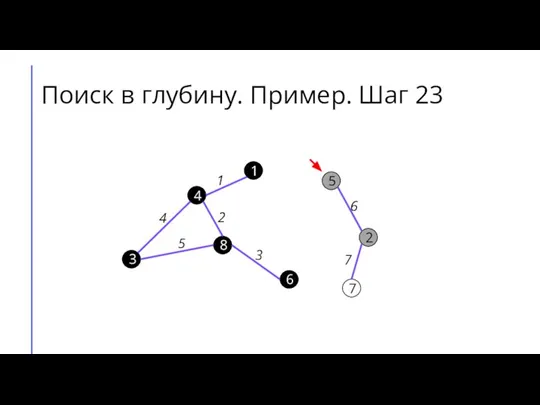
Слайд 31Поиск в глубину. Пример. Шаг 24
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
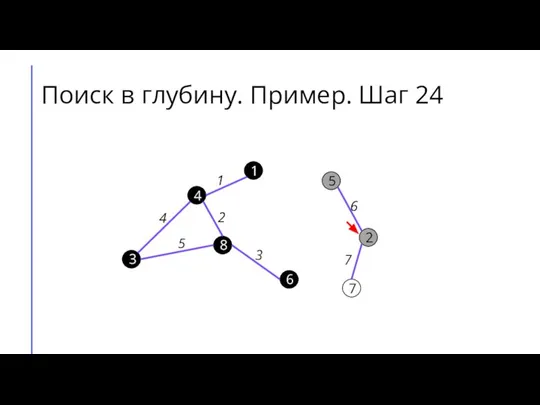
Слайд 32Поиск в глубину. Пример. Шаг 25
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Слайд 33Поиск в глубину. Пример. Шаг 26
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Слайд 34Поиск в глубину. Пример. Шаг 27
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Слайд 35Поиск в глубину. Пример. Шаг 28
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Слайд 36Поиск в глубину. Пример. Шаг 29
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Слайд 37Поиск в глубину. Пример. Шаг 30
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Слайд 38Хранение графа в программе
Создадим собственную структуру Node для хранения информации о вершине

графа.
В Node будем хранить цвет самой вершины и перечень смежных вершин.
Граф будем хранить в виде массива (вектора) вершин.
Слайд 39Реализация поиска в глубину
Поиск в глубину реализуется в виде рекурсивной функции, критерием

остановки которой является повторное посещение вершины.






































 Информация и её кодирование
Информация и её кодирование Проект Змейка с изменяемыми размерами карты
Проект Змейка с изменяемыми размерами карты Демилитаризованная зона DMZ (Demilitarized Zone
Демилитаризованная зона DMZ (Demilitarized Zone Форматирование графических изображений в Microsoft office
Форматирование графических изображений в Microsoft office Урок-викторина Счастливый случай (11 класс)
Урок-викторина Счастливый случай (11 класс) Разбор олимпиадных задач школьного этапа
Разбор олимпиадных задач школьного этапа Сумська обласна наукова медична бібліотека
Сумська обласна наукова медична бібліотека Смыслы в региональной журналистике
Смыслы в региональной журналистике prez_0
prez_0 Понятие информационной безопасности
Понятие информационной безопасности Програмирование в сфере офисных приложениях. Тенденции развития программного обеспечения
Програмирование в сфере офисных приложениях. Тенденции развития программного обеспечения Сервисы для INSMO
Сервисы для INSMO Вирусы и антивирусные программы
Вирусы и антивирусные программы Liver tumor
Liver tumor Автоматизация и диспетчеризация систем вентиляции
Автоматизация и диспетчеризация систем вентиляции Исполнитель робот. Ветвления. Урок 6
Исполнитель робот. Ветвления. Урок 6 Лайфхаки в Word
Лайфхаки в Word Система управления базами данных моделирование и формализация
Система управления базами данных моделирование и формализация Национальная Электронная Библиотека (НЭБ)
Национальная Электронная Библиотека (НЭБ) Понятие алгоритма
Понятие алгоритма Программная обработка данных. 8 класс
Программная обработка данных. 8 класс Программы автоматизированного перевода текста
Программы автоматизированного перевода текста Прерывания
Прерывания AutoCAD: история и возможности
AutoCAD: история и возможности Триггеры в презентации. Применение
Триггеры в презентации. Применение Отчёты. Лекция 6
Отчёты. Лекция 6 Создание и разработка мобильной игры
Создание и разработка мобильной игры Интегрированная система электронного документооборота, архива и управления потоками работ
Интегрированная система электронного документооборота, архива и управления потоками работ