Содержание
- 2. Хэш – функция с точки зрения компьютерных наук – функция, осуществляющая преобразование массива входных данных произвольной
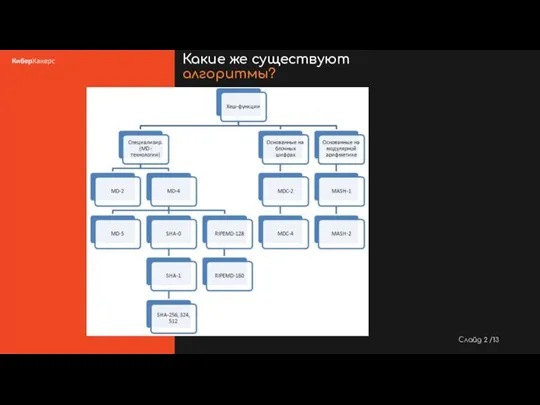
- 3. Слайд /13 Какие же существуют алгоритмы?
- 4. Слайд /13 SHA - 256
- 5. Слайд /13 Шаг 1 - Пролог Возмём строку “hello world”, переведём её в двоичный формат. Затем
- 6. Слайд /13 Шаг 2 – Инициализируем значения хэша (h) Теперь мы создаем 8 хэш-значений. Это жестко
- 7. Слайд /13 Шаг 3 - Инициализируем округленные константы (k) Как и в предыдущем шаге, мы создадим
- 8. Слайд /13 Шаг 4 — Цикл фрагментов Следующие шаги будут выполняться для каждого 512-битного «фрагмента» из
- 9. Слайд /13 Шаг 5 — Созданием расписание сообщений (w) Скопируем входные данные из шага 1 в
- 10. Слайд /13 Шаг 6 — Сжатие Инициализируем переменные a, b, c, d, e, f, g, h
- 11. Слайд /13 Шаг 7 — Изменим окончательные значения После цикла сжатия, во время цикла фрагментов, мы
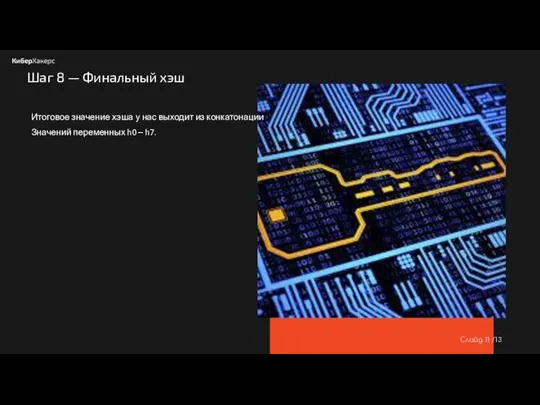
- 12. Слайд /13 Шаг 8 — Финальный хэш Итоговое значение хэша у нас выходит из конкатонации Значений
- 13. Слайд /13 Методы взлома хэш - функций Поиск первого прообраза Поиск второго прообраза Поиск коллизии Так
- 15. Скачать презентацию










 Презентация на тему Издательская программа PageMaker
Презентация на тему Издательская программа PageMaker  Решение задач
Решение задач Всеукраїнське друковане інформаційне видання для безкоштовного розповсюдження у поїздах Інтерсіті +, СВ
Всеукраїнське друковане інформаційне видання для безкоштовного розповсюдження у поїздах Інтерсіті +, СВ Курс SEO-практик. Управление индексацией сайта. Дубли и служебные страницы
Курс SEO-практик. Управление индексацией сайта. Дубли и служебные страницы Интеграция в Windows
Интеграция в Windows циклы Обмена отчеты ФНС
циклы Обмена отчеты ФНС Задания КИМ с решениями
Задания КИМ с решениями Правило Если - то
Правило Если - то Решение логической задачи соки. Рабочая тетрадь №41 стр.36
Решение логической задачи соки. Рабочая тетрадь №41 стр.36 Игра MegaMemory2
Игра MegaMemory2 Информационная безопасность
Информационная безопасность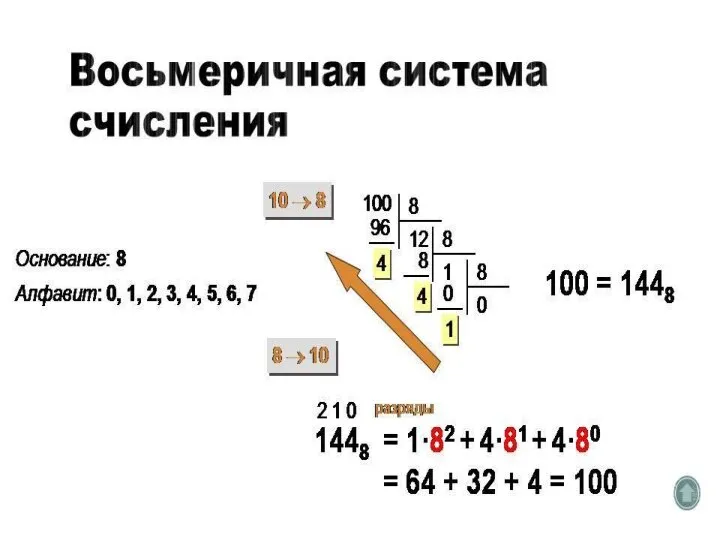 10 класс системы счисления сложение
10 класс системы счисления сложение 12_Строки
12_Строки Система электронного архива
Система электронного архива 30 ноября – международный день защиты информации
30 ноября – международный день защиты информации Система распознавания лиц для контроля доступа на объект
Система распознавания лиц для контроля доступа на объект Инсталляция и эксплуатация вычислительных машин и систем
Инсталляция и эксплуатация вычислительных машин и систем Сетевые технологии, протоколы, утилиты
Сетевые технологии, протоколы, утилиты Інформаційна система обліку досягнень у тренажерному залі
Інформаційна система обліку досягнень у тренажерному залі Этапы параллельного программирования. Лекция 6
Этапы параллельного программирования. Лекция 6 4 Двоичное кодирование
4 Двоичное кодирование Контроль качества
Контроль качества Содержательный процесс разработки ассемблерной программы. (Лекция 8)
Содержательный процесс разработки ассемблерной программы. (Лекция 8) Безопасность детей в Интернете
Безопасность детей в Интернете Ковид19стф.рф –
Ковид19стф.рф – Magazines Today
Magazines Today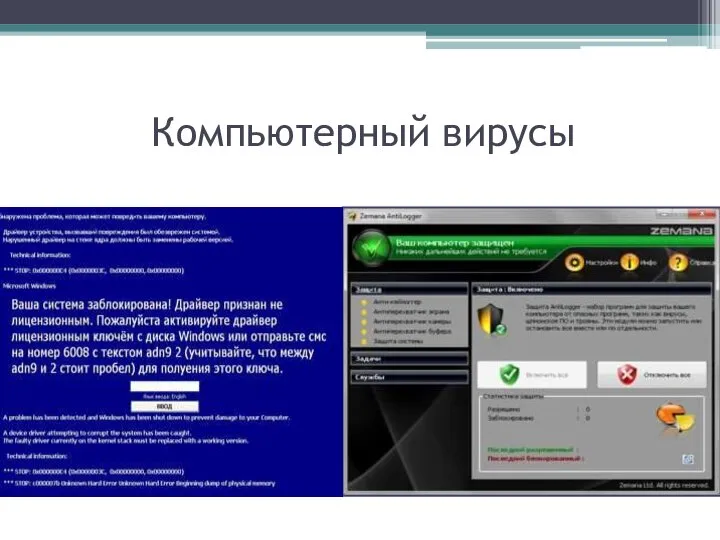 Компьютерный вирусы
Компьютерный вирусы Варианты построения алгоритмов
Варианты построения алгоритмов