Контекстно-свободные языки и грамматики. Лекция 4

План лекции
1 Вывод цепочек
2 Дерево разбора
3 Однозначность КС-грамматик

1 Вывод цепочек
Пример 1. Дано: G=({a, b, +}, {S, T},
{S→T|T+S; T → a|b}, S)
Построить: вывод цепочки a+b+a
Левосторонний вывод:
Правосторонний вывод:
S⇒
T+S ⇒
a+S ⇒
a+T+S ⇒
a+b+S ⇒
a+b+T ⇒
a+b+a
S ⇒
T+S ⇒
T+T+S ⇒
T+T+T ⇒
T+T+a ⇒
T+b+a ⇒
a+b+a

2 Дерево разбора
(1) {VT∪VN ∪ ε},
(2) A∈ VN ,
(3) A∈ VN ,
S,
{VT ∪ ε }
a1, a2, …, an , ai ∈{VT∪VN }
A→a1a2…an ∈Р, n≥1
ε,
A→ ε ∈Р

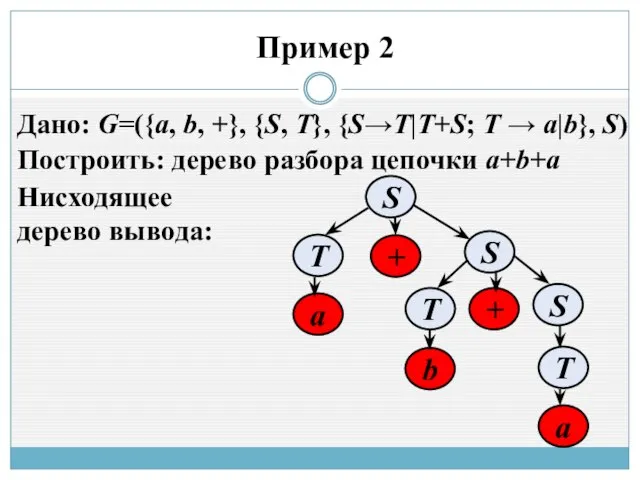
Пример 2
Построить: дерево разбора цепочки a+b+a
Дано: G=({a, b, +}, {S, T}, {S→T|T+S; T → a|b}, S)
Нисходящее дерево вывода:
T
+
a
b
+
a
T
S
S
S
T

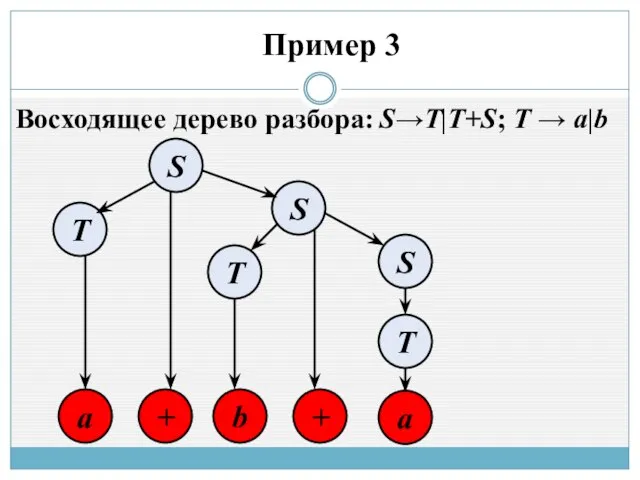
S
T
+
a
T
b
a
+
S
Пример 3
Восходящее дерево разбора:
S
S→T|T+S; T → a|b
T

3 Однозначность КС-грамматик
(1) A → AA | α
(2) A → AαA | β
(3) A → αA | Aβ | γ
(4) A → αA | αAβA | γ
где A∈VN; α, β, γ ∈V*.