Содержание
- 2. Компьютер и его функциональное устройство
- 3. Компьютер – это техническое средство преобразования информации, в основу работы которого заложены те же принципы обработки
- 4. С позиции функционального назначения компьютер – это система, состоящая из 4-х основных устройств, выполняющих определенные функции:
- 5. Запоминающее устройство (память) предназначается для хранения информации и команд программы в ЭВМ. Информация, которая хранится в
- 6. Виды памяти Внутренняя ОЗУ ПЗУ Внешняя Диски Флешки Дискеты Магнитные ленты
- 7. Арифметико-логическое устройство (АЛУ). Производит арифметические и логические действия. Следует отметить, что любую арифметическую операцию можно реализовать
- 8. Устройство управления (УУ) управляет всем ходом вычислительного и логического процесса в компьютере, т.е. выполняет функции "регулировщика
- 9. В современных компьютерах функции УУ и АЛУ выполняет одно устройство, называемое центральным процессором.
- 10. Устройства ввода и вывода - устройства взаимодействия компьютера с внешним миром: с пользователями или другими компьютерами.
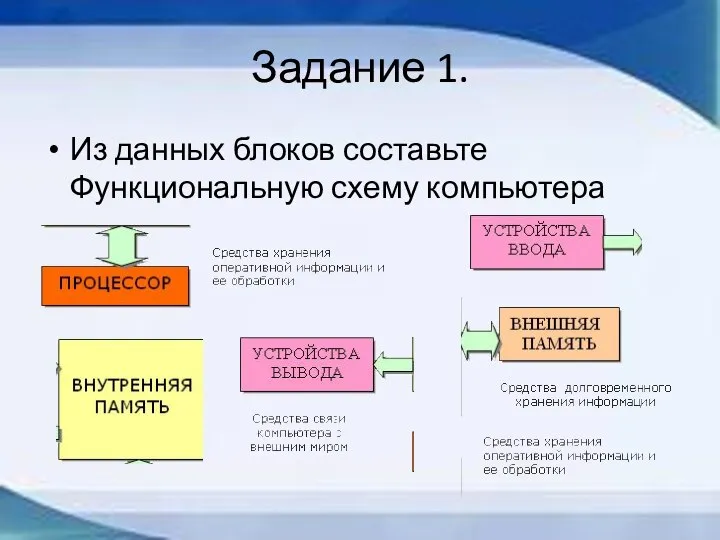
- 11. Задание 1. Из данных блоков составьте Функциональную схему компьютера
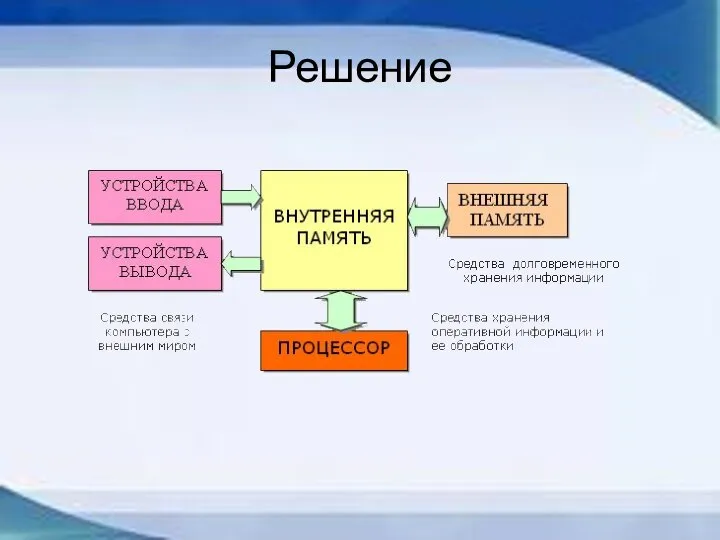
- 12. Решение
- 13. АРИФМЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ ЭВМ
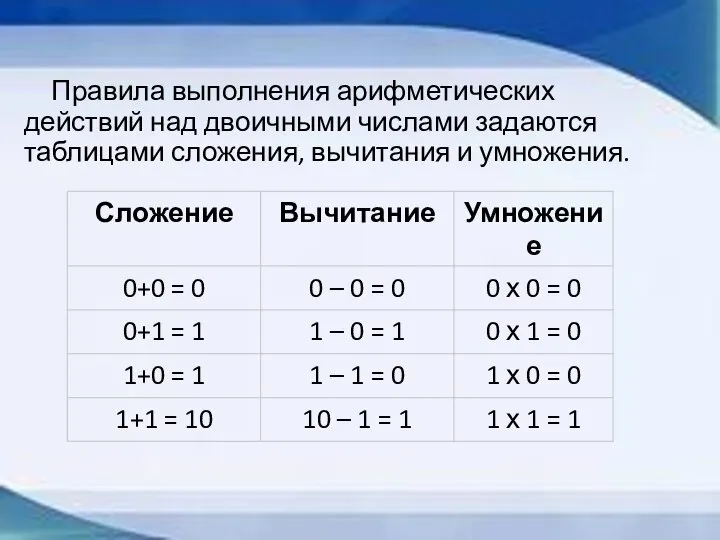
- 14. Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения.
- 15. Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов
- 16. Вся информация в компьютере представлена в виде двоичного кода. Компьютер переводит информацию (числовую, текстовую, графическую, звуковую,
- 17. Алгоритм перевода: Двоичное число записать в развернутой форме. Давайте вернемся в курс математики и вспомним, как
- 18. Задание 2 1. Переведите числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.
- 19. Алгебра логики Булева алгебра оперирует логическими переменными, которые могут принимать только два значения: истина или ложь
- 20. Логической функцией называется функция, которая может принимать только 2 значения – истина или ложь (1 или
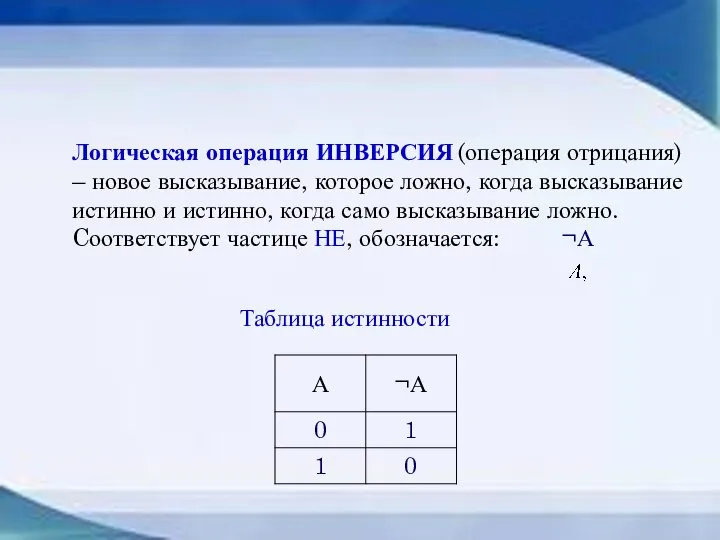
- 21. Таблица истинности Логическая операция ИНВЕРСИЯ (операция отрицания) – новое высказывание, которое ложно, когда высказывание истинно и
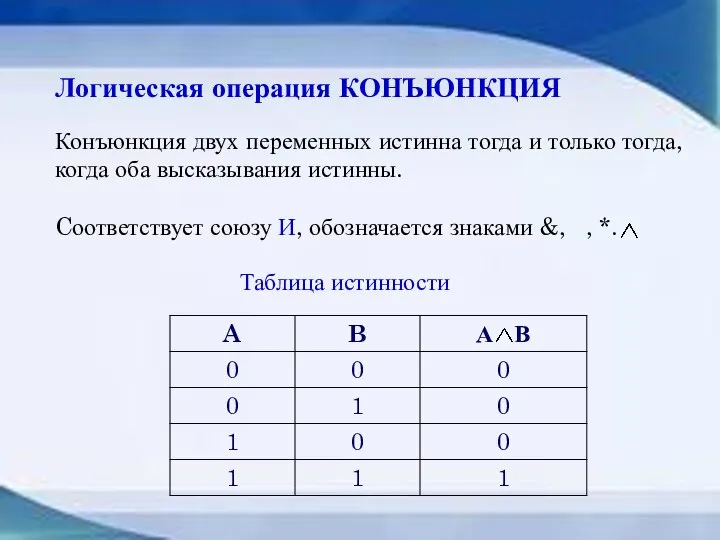
- 22. Логическая операция КОНЪЮНКЦИЯ Конъюнкция двух переменных истинна тогда и только тогда, когда оба высказывания истинны. Cоответствует
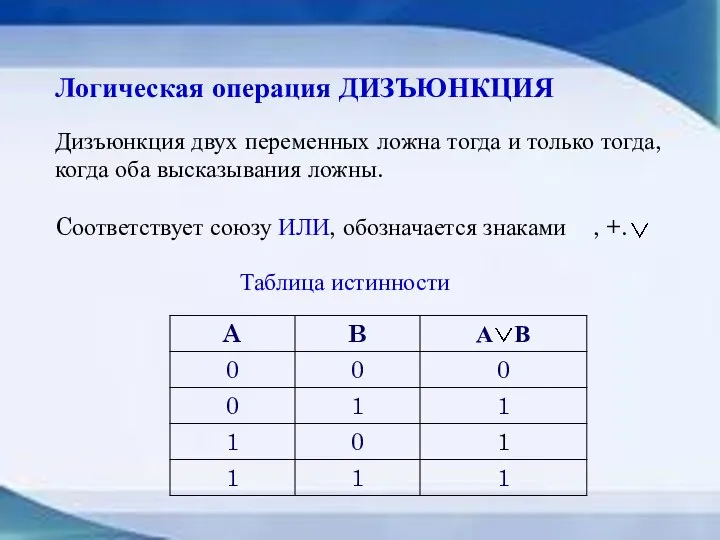
- 23. Логическая операция ДИЗЪЮНКЦИЯ Дизъюнкция двух переменных ложна тогда и только тогда, когда оба высказывания ложны. Cоответствует
- 24. Алгоритм
- 25. Алгоритм – система точных и понятных предписаний (команд, инструкций, директив) о содержании и последовательности выполнения конечного
- 26. Свойства алгоритма Дискретность (от лат. discretus – разделенный, прерывистый) указывает, что любой алгоритм должен состоять из
- 27. Типовые конструкции алгоритмов: Линейный. Циклический. Разветвляющийся. Вспомогательный.
- 28. Линейный (последовательный) алгоритм – описание действий, которые выполняются однократно в заданном порядке. Циклический – описание действий
- 29. Способы описания алгоритмов. на естественном языке; на специальном (формальном) языке; с помощью формул, рисунков, таблиц; с
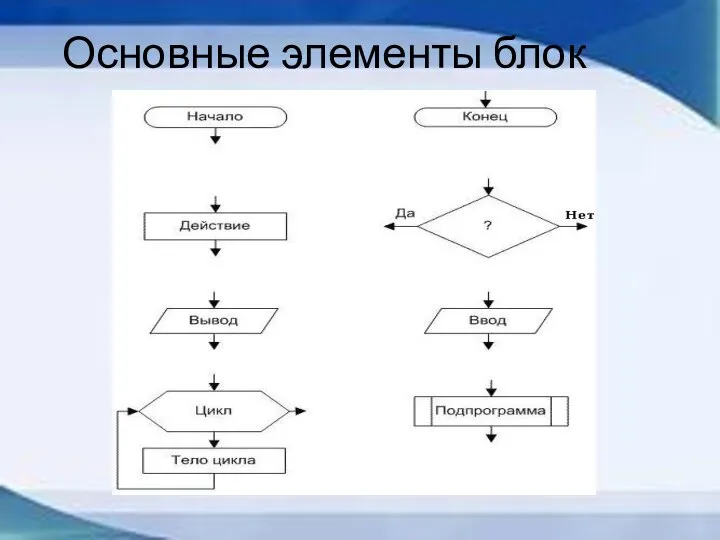
- 30. Основные элементы блок схемы
- 31. Задание 3 Составьте блок-схему для решения полного квадратного уравнения ax2+bx+c=0/
- 33. Скачать презентацию























 Настройка динамической маршрутизации на базе протокола RIP на ободуровании MikroTik
Настройка динамической маршрутизации на базе протокола RIP на ободуровании MikroTik 声明:此工具仅针对平台分离式
声明:此工具仅针对平台分离式 Сайт для голосований “Simple votings”
Сайт для голосований “Simple votings” Информационная безопасность
Информационная безопасность Методы работы с источниками информации Неграмотным человеком завтрашнего дня будет не тот, кто не умеет читать, а тот, кто не научи
Методы работы с источниками информации Неграмотным человеком завтрашнего дня будет не тот, кто не умеет читать, а тот, кто не научи Исследование функций и построение графиков
Исследование функций и построение графиков Архитектура компьютера с хранимой программой
Архитектура компьютера с хранимой программой The Internet. Week -1
The Internet. Week -1 Как работает поисковая машина
Как работает поисковая машина 8-3py_Массивы (Python)_2
8-3py_Массивы (Python)_2 Файлы и файловые структуры
Файлы и файловые структуры Подготовили Батуева Л.Н.-учитель математики МБОУ СОШ №11 г.Чайковский , Маркова Е.В- учитель информатики МБОУ СОШ №11 г.Чайковск
Подготовили Батуева Л.Н.-учитель математики МБОУ СОШ №11 г.Чайковский , Маркова Е.В- учитель информатики МБОУ СОШ №11 г.Чайковск E-Liibrary и РИНЦ. Новые вызовы научному сообществу в связи с образовательными реформами
E-Liibrary и РИНЦ. Новые вызовы научному сообществу в связи с образовательными реформами Компьютерная память
Компьютерная память Основные определения и критерии классификации угроз безопасности информации
Основные определения и критерии классификации угроз безопасности информации Презентация на тему Электронный документ и файл
Презентация на тему Электронный документ и файл  Презентация на тему Построение диаграмм и графиков
Презентация на тему Построение диаграмм и графиков  Ссылка в html-документе
Ссылка в html-документе Эффективная работа с информацией
Эффективная работа с информацией Как перенести информацию из внешнего мира на какой-либо носитель
Как перенести информацию из внешнего мира на какой-либо носитель Цифровая картографическая информация. Лекция №04
Цифровая картографическая информация. Лекция №04 Упаковка и распаковка данных с помощью программ-архиваторов. WinRAR
Упаковка и распаковка данных с помощью программ-архиваторов. WinRAR Мастер класс. Файл. Файловая система
Мастер класс. Файл. Файловая система Массивы в языке Си
Массивы в языке Си Интерактивные и мультимедийные технологии в музее
Интерактивные и мультимедийные технологии в музее CryptoBox. Применение шифрования
CryptoBox. Применение шифрования Вирусы и борьба с ними
Вирусы и борьба с ними Лекция 4
Лекция 4