Слайд 2Линейные списки
Линейным списком называется упорядоченная структура, каждый элемент которой связан с

соседним элементом. Наибольшее распространение получили два вида линейных списков: стеки и очереди.
Стек это список типа LIFO (последним пришел – первым вышел). Стек имеет одну точку доступа, которая называется вершиной.
Аналогом стека является стопка книг, в которой дополнение и изъятие книг происходит сверху.
Другим примером может служить обойма с патронами (магазин), в которой зарядка и подача для стрельбы выполняется с одного конца. Именно этим примером объясняется бывшее в употреблении русскоязычное название стека “магазин”.
В программировании через стеки передаются параметры при обращении к процедурам. Если имеется цепочка вызова функций, то локальные переменные могут сохраняться в стеке, который расширяется при загрузке функции и сокращается при возврате из нее.
Иногда стеки реализуются аппаратным образом. В Ассемблере имеется регистр стека и соответствующие команды для работы с ним.
Слайд 3Стеки: представление в ОП
Стеки могут представляться как в статической, так и

динамической памяти. В статическом представлении стек задается одномерным массивом, величина которого определяется с запасом. Пусть он описан в виде Var Stack[1..N] of T, где T – тип элементов стека. Вершина стека задается индексом массива Top.
Дополнение в стек (push) производится командами
Top := Top+1;
Stack[Top] := NewElement;
Удаление из стека (pop) выполняется командой Top:= Top-1.
Для обработки возможных ошибок при дополнении необходимо проверять выход за границы массива, а при удалении проверять непустоту стека.
Признаком пустого стека при индексации с 1 является условие Top = 0.
Слайд 4Стеки: представление в ОП
В динамической памяти стек представляется в виде
Type
Ukaz

= ^Stek;
Stek = record
name: string;
next: ukaz;
end;
Var
Top, Kon: ukaz;
Здесь в качестве примера информационная часть элементов описана переменной name, а указатель next обеспечивает связь с предыдущим элементом.
Слайд 5Операции со стеками
Включение в стек (push) реализуется командами
New(Kon); { создание

элемента, на который указывает Kon }
Kon^.next:=Top;
Kon^.name:=NewName;
Top:=Kon;
Удаление из стека (pop):
Kon:=Top;
Top:=Top^.next;
Dispose(Kon); { удаление бывшей вершины стека }
Операции push и pop обычно оформляют в виде функций или процедур. Признаком пустого стека является условие Top = nil.
Слайд 6Операции со стеками
Обычно изменение стека идет через его вершину. Для демонстрации
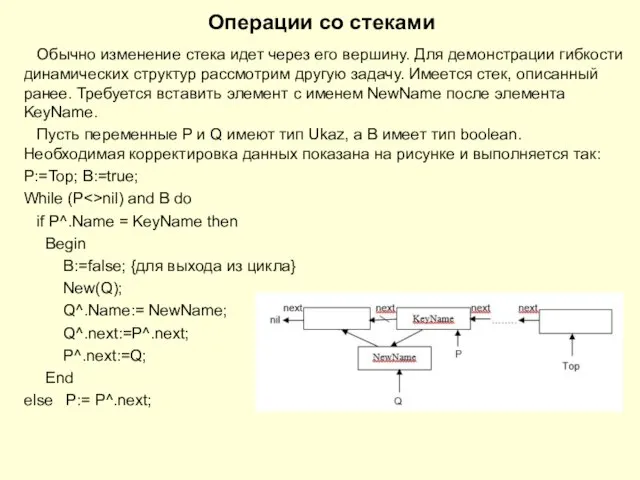
гибкости динамических структур рассмотрим другую задачу. Имеется стек, описанный ранее. Требуется вставить элемент с именем NewName после элемента KeyName.
Пусть переменные P и Q имеют тип Ukaz, а B имеет тип boolean. Необходимая корректировка данных показана на рисунке и выполняется так:
P:=Top; B:=true;
While (P<>nil) and B do
if P^.Name = KeyName then
Begin
B:=false; {для выхода из цикла}
New(Q);
Q^.Name:= NewName;
Q^.next:=P^.next;
P^.next:=Q;
End
else P:= P^.next;
Слайд 7Операции со стеками
А теперь видоизменим задачу. Пусть вставка требуется перед элементом
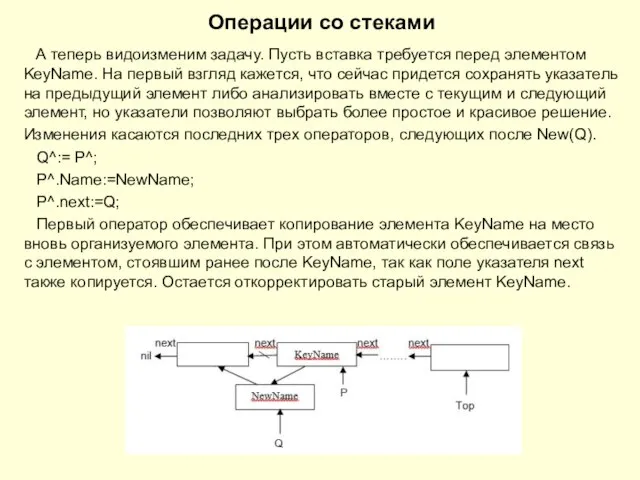
KeyName. На первый взгляд кажется, что сейчас придется сохранять указатель на предыдущий элемент либо анализировать вместе с текущим и следующий элемент, но указатели позволяют выбрать более простое и красивое решение.
Изменения касаются последних трех операторов, следующих после New(Q).
Q^:= P^;
P^.Name:=NewName;
P^.next:=Q;
Первый оператор обеспечивает копирование элемента KeyName на место вновь организуемого элемента. При этом автоматически обеспечивается связь с элементом, стоявшим ранее после KeyName, так как поле указателя next также копируется. Остается откорректировать старый элемент KeyName.
Слайд 8Формы представления алгебраических выражений
Постфиксная запись представляет собой такую запись алгебраического выражения,

в которой сначала записываются операнды, а затем – знак операции.
Например, для выражения a + b * c постфиксная запись будет a b c * +. Здесь операндами операции * будут b и c (два ближайших операнда), а операндами операции + будут а и составной операнд b c *.
Эта запись удобна тем, что она не требует скобок. Например, для выражения (a + b) * c постфиксная запись будет a b + c *. В этой записи не требуется ставить скобки для того, чтобы изменить порядок вычисления, зависящий от приоритета операций, как в исходном выражении. Поэтому постфиксная запись удобна для вычисления алгебраических выражений и широко применяется на практике.
В префиксной записи сначала наоборот записывается знак операции, а затем операнды. Например, для выражения a + b * c префиксная запись будет + a * b c.
Префиксная запись также не требует расстановки скобок. Префиксную форму называют еще польской записью, а постфиксную – обратной польской записью.
Слайд 9Формы представления алгебраических выражений
Привычная форма записи со скобками называется инфиксной.
Выражение

может включать как двуместные операции, так и одноместные. Примерами одноместных операций могут быть функции.
Вычислить значение выражения, записанного в постфиксной записи, очень просто. Требуется единственный последовательный просмотр символов (лексем) выражения.
Просматриваем постфиксную запись. Значения переменных и констант кладутся в стек. Когда встречается операция, из стека берутся два верхних (последних) значения, вычисляется результат применения операции к этим значениям, и результат помещается в стек. Если встречается функция, то берётся одно значение из стека, а результат помещается в стек на его место.
Например, выражение в постфиксной форме a b c + * d – sin соответствует инфиксной форме sin (a * (b + c) - d) и вычисляется в порядке, задаваемом скобками.
Слайд 10Алгоритм Дейкстры преобразования
выражения из инфиксной формы в постфиксную
Алгоритм Дейкстры перевода в

постфиксную запись обрабатывает исходный массив лексем и строит новый массив из тех же лексем, расположенных в другом порядке. Кроме того, необходим еще стек – аналогичный массив, используемый для временного хранения операций.
Операции имеют разные приоритеты. Наименьший приоритет у операций ‘+’ и ‘-‘. Более высокий приоритет имеют операции ‘*’ и ‘/’. Еще более высокий приоритет у операции возведения в степень ‘^’. Самый высокий приоритет имеют операции, задаваемые функциями, такими как ‘sin‘, ‘cos’, ‘exp’. Заметим, что для этих операций требуется единственный операнд.
Если операнд представляет собой выражение с другими знаками операций, то он должен заключаться в скобки.
Слайд 11Алгоритм Дейкстры преобразования
выражения из инфиксной формы в постфиксную

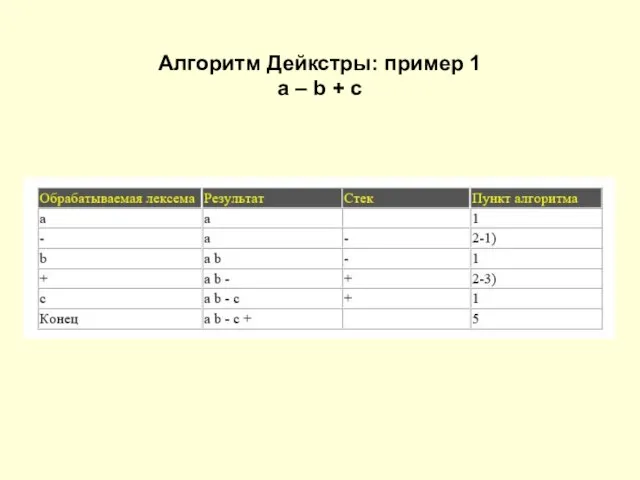
Слайд 12Алгоритм Дейкстры: пример 1
a – b + c
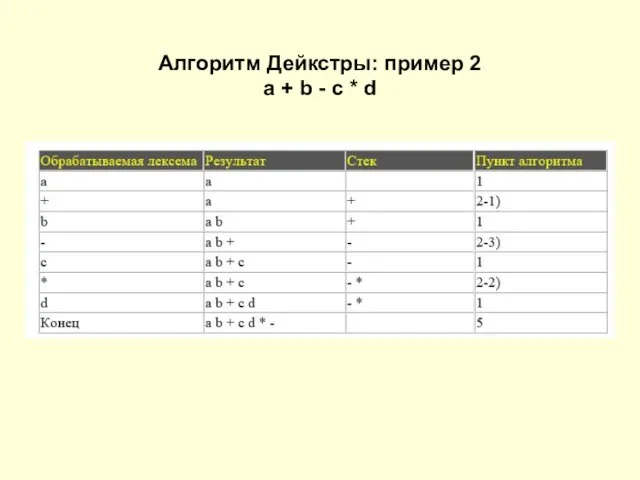
Слайд 13Алгоритм Дейкстры: пример 2
a + b - c * d
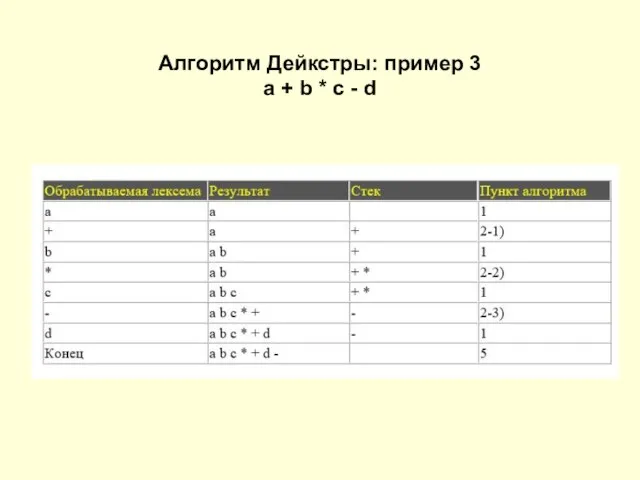
Слайд 14Алгоритм Дейкстры: пример 3
a + b * c - d
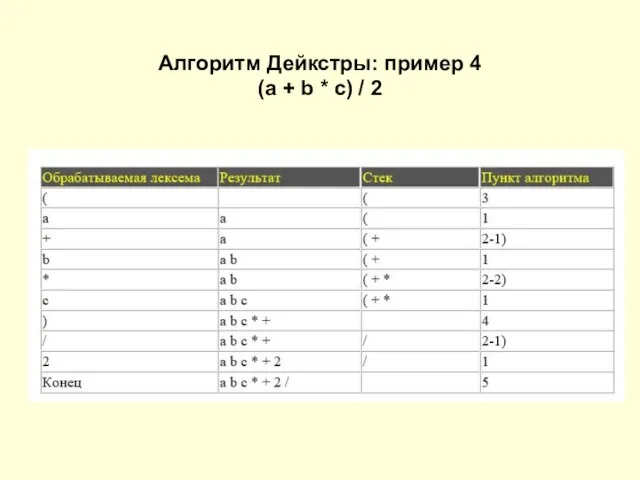
Слайд 15Алгоритм Дейкстры: пример 4
(a + b * c) / 2
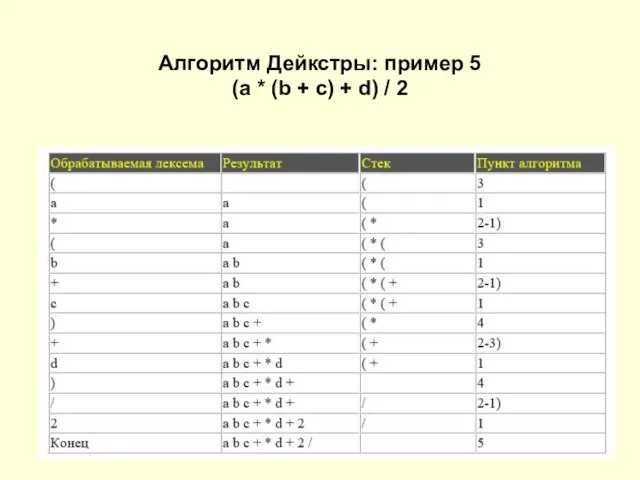
Слайд 16Алгоритм Дейкстры: пример 5
(a * (b + c) + d) / 2
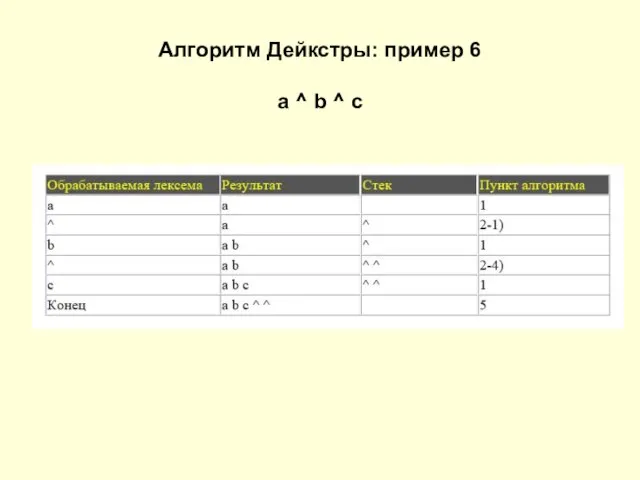
Слайд 17Алгоритм Дейкстры: пример 6
a ^ b ^ c
Слайд 18Алгоритм Дейкстры: пример 7
sin cos a
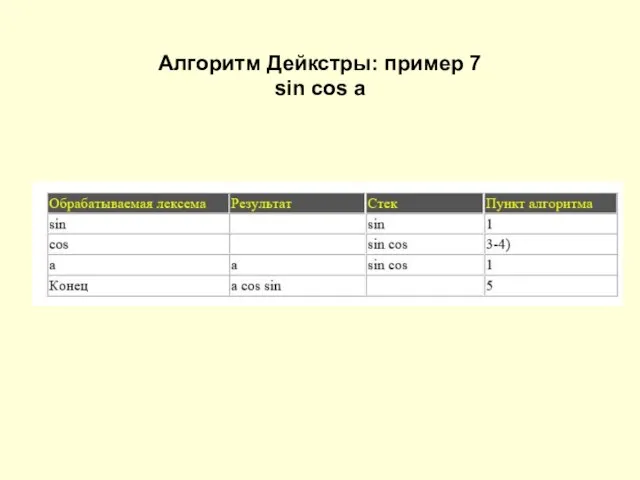
Слайд 19Алгоритм Дейкстры: пример 8
exp(a * ln b)
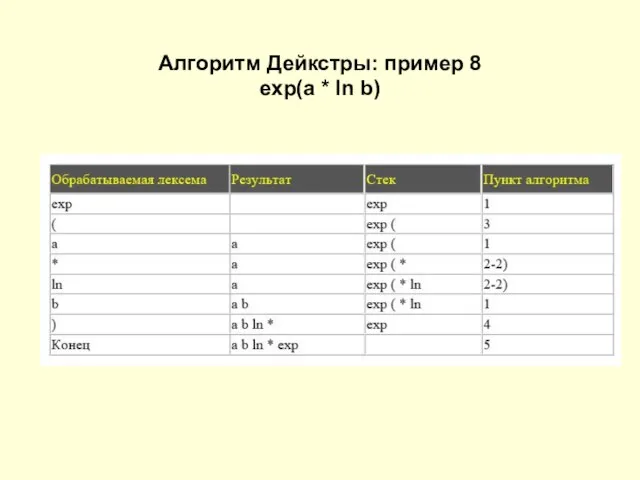
Слайд 20Алгоритм Дейкстры: пример 9
sin a ^ b
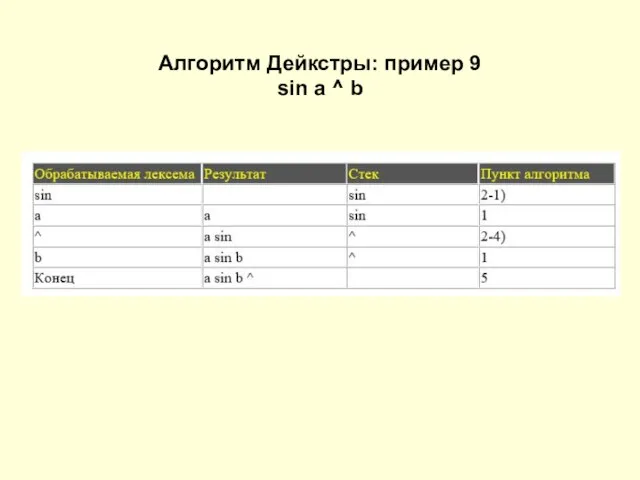
Слайд 21Вычисление выражения a b c + * d + 2 /
а =
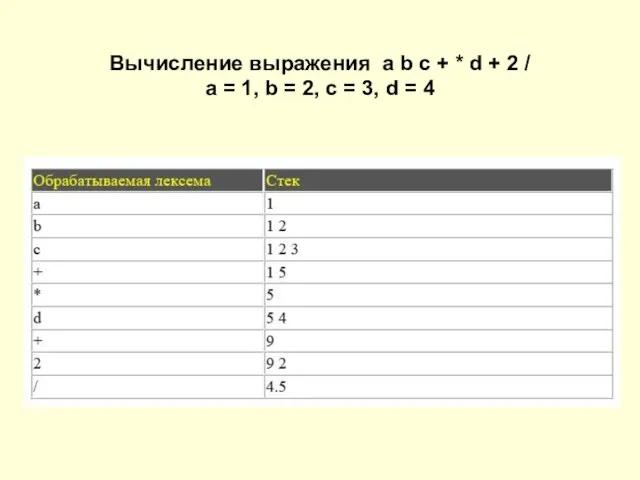
Слайд 22Вычисление выражения x x sin 2 * +
x = 3.14

Слайд 23Операции со стеком на C++
#include
using namespace std;
struct St
{
int key;
St *next;
};
void

push(St *&p, int elem); // включение в стек (p меняется)
void pop(St *&p); // удаление из стека (p меняется)
void vivod(St *p); // вывод содержимого стека на экран (p не меняется)
void clear(St *p); // очистка стека (p не меняется)
int main()
{
setlocale(LC_ALL, "rus");
system("cls");
St *top=0; // признак пустого стека
int answer = 1;
Слайд 24Операции со стеком на C++
while (answer != 5)
{
printf("\n1 Включение в стек");
printf("\n2

Удаление из стека");
printf("\n3 Выдача стека");
printf("\n4 Удаление всего стека");
printf("\n5 Конец");
printf("\nВаш выбор? ");
cin >> answer;
switch (answer)
{
case 1: // Включение в стек
int k;
printf("Введите целое число ");
cin >> k;
push(top, k);
break;
case 2: // Удаление из стека
if (top)
{
pop(top);
}
else printf("Стек пуст\n");
break;
Слайд 25Операции со стеком на C++
case 3: // Вывод на экран
if (top)
{
vivod(top);
}
else

printf("Стек пуст\n");
break;
case 4: // Очистка стека
if (top)
{
clear(top);
}
else printf("Стек пуст\n");
top = 0; // функция clear не возвращает top!
break;
case 5:
clear(top); // Сначала очистка стека
top = 0; // функция clear не возвращает top!
break;
}
}
return 0;
}
























 Серия игр S.T.A.L.K.E.R
Серия игр S.T.A.L.K.E.R ArtStyle Group. Комплексные решения. Проектирование и разработка веб-сайтов
ArtStyle Group. Комплексные решения. Проектирование и разработка веб-сайтов Homework assignment
Homework assignment Оптоволоконные сети
Оптоволоконные сети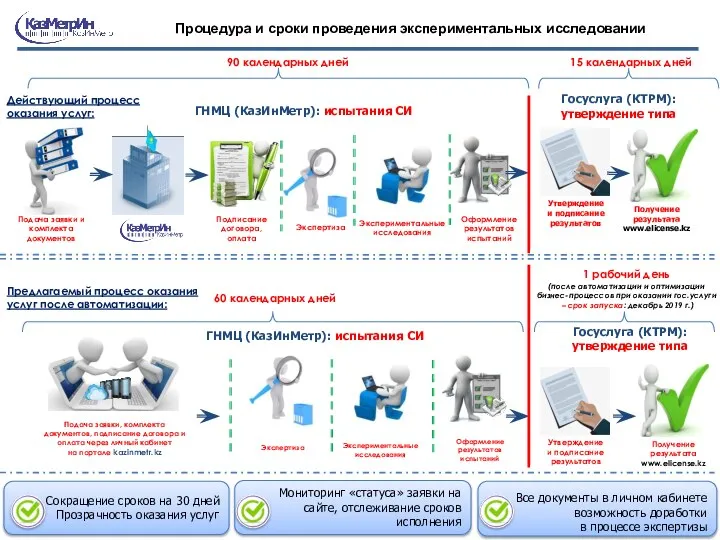 Аттестация поверителей. Процедура и сроки проведения экспериментальных исследований
Аттестация поверителей. Процедура и сроки проведения экспериментальных исследований Утиліта CCleaner
Утиліта CCleaner Игра как искусство: манифест Ice-Pick Lodge
Игра как искусство: манифест Ice-Pick Lodge Создание приложения Конвертер графических изображений на языке С++
Создание приложения Конвертер графических изображений на языке С++ Введение в профессию web - разработчика
Введение в профессию web - разработчика Мой инструмент компьютер
Мой инструмент компьютер HTML и CSS. Введение
HTML и CSS. Введение Приложение LearningApps.org
Приложение LearningApps.org Компьютердің қауіпсіздік ережелері
Компьютердің қауіпсіздік ережелері Защита электронной документации
Защита электронной документации Время, потерянное с удовольствием, не считается потерянным
Время, потерянное с удовольствием, не считается потерянным Текст и его типы
Текст и его типы Язык Java
Язык Java Взаимодействие систем электронного документооборота
Взаимодействие систем электронного документооборота Алгоритм участия в акции Диктант Победы 2021
Алгоритм участия в акции Диктант Победы 2021 Одномерные массивы целых чисел. Алгоритмизация и программирование
Одномерные массивы целых чисел. Алгоритмизация и программирование Спам и защита от него
Спам и защита от него Программирование циклов. Оператор for
Программирование циклов. Оператор for Комплект UML диаграмм к системе. Работа DHCP сервера
Комплект UML диаграмм к системе. Работа DHCP сервера Социальные сети
Социальные сети Конкурс программистов
Конкурс программистов Алгоритмическая конструкция следование
Алгоритмическая конструкция следование Администрирование баз данных. Тема 5.1
Администрирование баз данных. Тема 5.1 Управление портами микроконтроллера в режиме ввода-вывода общего назначения (GPIO)
Управление портами микроконтроллера в режиме ввода-вывода общего назначения (GPIO)