Содержание
- 2. Некоторые задачи требуют введения структур, способных увеличивать или уменьшать свой размер в процессе работы программы. Основу
- 3. Если для связи элементов в структуре задан указатель (адресное поле) на следующий элемент, то такой список
- 4. Для работы с однонаправленными списками шаблон структуры (структурный тип) будет иметь следующий вид: struct TList1 {
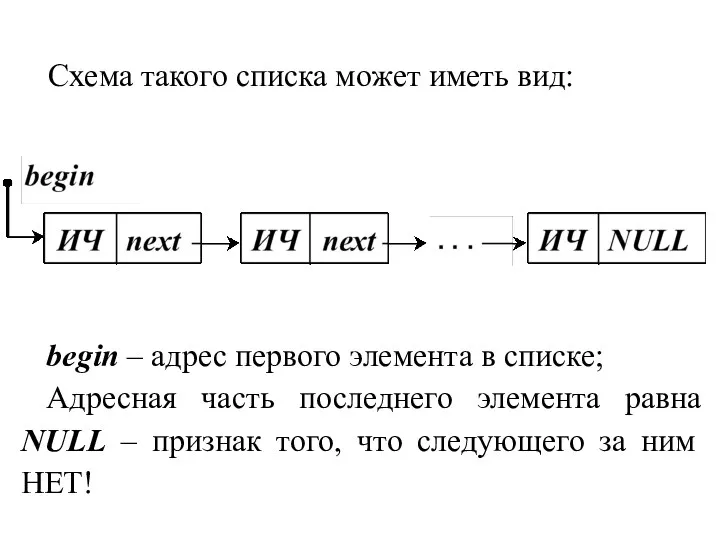
- 5. Схема такого списка может иметь вид: begin – адрес первого элемента в списке; Адресная часть последнего
- 6. Для работы с двунаправленными списками шаблон структуры будет иметь следующий вид: struct TList2 { Информационная часть
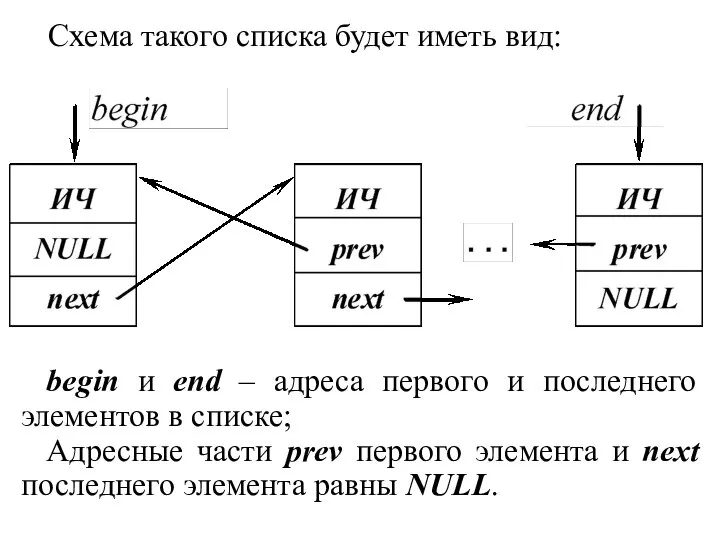
- 7. Схема такого списка будет иметь вид: begin и end – адреса первого и последнего элементов в
- 8. Над списками обычно выполняются следующие операции: – начальное формирование списка (создание первого элемента); – добавление нового
- 9. Структура данных СТЕК Стек – упорядоченный набор данных, в ко-тором добавление и удаление элементов производится только
- 10. Графически Стек можно изобразить так: Стек получил свое название из-за схожести с обоймой патронов: когда добавляется
- 11. Число элементов стека не ограничивается. При добавлении элементов в стек память должна динамически выделяться и освобождаться
- 12. Кроме этих обязательных операций используется операция top (peek) для чтения информации в вершине стека без извлечения.
- 13. Алгоритм формирования стека Рассмотрим данный алгоритм для первых двух элементов. 1. Описание типа для структуры, содержащей
- 14. 2. Объявление указателей на структуру (можно объявить в шаблоне глобально): Stack *begin, – Вершина стека *t;
- 15. 5. Ввод информации (обозначим i1); а) формирование информационной части: t -> info = i1; б) формирование
- 16. 6. Вершина стека переносится на созданный первый элемент: begin = t; В результате получается следующее: 7.
- 17. 8. Ввод информации для второго элемента (i2); а) формирование информационной части: t -> info = i2;
- 18. 9. Вершина стека снимается с первого и устанавливается на новый элемент (A2): begin = t; Получается
- 19. Функция формирования элемента стека Простейший вид функции (типа push), в которую передаются указатель на вершину (р)
- 20. Участок программы с обращением к функции InStack для добавления n элементов (исполь-зуем случайные числа) в стек
- 21. Если в функцию InStack указатель на вершину передавать по адресу, то она может иметь следующий вид:
- 22. Просмотр стека (без извлечения) 1. Устанавливаем текущий указатель на вершину t = begin; 2. Проверяем, если
- 23. 4. ИЧ текущего элемента t -> info выводим на экран. 5. Переставляем текущий указатель t на
- 24. Функция, реализующая этот алгоритм: void View (Stack *p) { Stack *t = p; if ( p
- 25. Алгоритм освобождения памяти 1. Начинаем цикл, выполняющийся пока begin не станет равным NULL. 2. Устанавливаем текущий
- 26. Функция, реализующая этот алгоритм, может иметь следующий вид: void Del_All ( Stack **p ) { Stack
- 27. Параметром данной функции является указатель на указатель, т.е. в функцию передаем адрес указателя на вершину стека
- 28. Эту функцию можно реализовать и иначе: Stack* Del_All ( Stack *p ) { Stack *t; while
- 29. В данном случае в функцию передаем указатель на вершину стека, а его измененное значение, равное NULL,
- 30. Алгоритм получения информации из вершины стека c извлечением 1. Устанавливаем текущий указатель t на вершину t
- 31. Функция (типа pop), в которую передаются вершина (р) и адрес переменной out для интересующей нас информации,
- 32. Обращение к этой функции: begin = OutStack ( begin, &out ); Необходимая нам информация out (в
- 33. int OutStack ( Stack **p ) { int out ; Stack *t = *p; out =
- 34. Рассмотрим примеры удаления из стека элементов, кратных 5. Текст функции удаления непосредственно из стека может иметь
- 35. Stack* Del_5(Stack *b) { b = InStack (b, 21); // Добавляем любое число Stack *p =
- 36. else { p = t; t = t -> next; } } t = b; //
- 37. Указатель на вершину стека передаем в функцию, а его измененное значение, возвращаем из функции в точку
- 38. Stack* Del_5_mas (Stack *b) { int n = 0, *a, i, m; Stack *t = b;
- 39. a = new int[n]; // Создаем динамический массив // Извлекаем все элементы из стека в массив
- 40. /* Создаем стек снова – переписываем в него элементы, оставшиеся в массиве: */ for ( i
- 41. И в этом случае в функцию передаем указатель на вершину стека, а его измененное значение, возвращаем
- 42. Stack* New_Stack_5 (Stack *b) { int inf; Stack *new_b = NULL; while (b != NULL) {
- 43. Обращение к функции: begin = New_Stack_5 ( begin ); Линейный поиск нужной информации в стеке может
- 44. int Poisk (Stack *p) { int k = 0; Stack *t = p; while( t !=
- 46. Скачать презентацию



































![a = new int[n]; // Создаем динамический массив // Извлекаем все элементы](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/948067/slide-38.jpg)




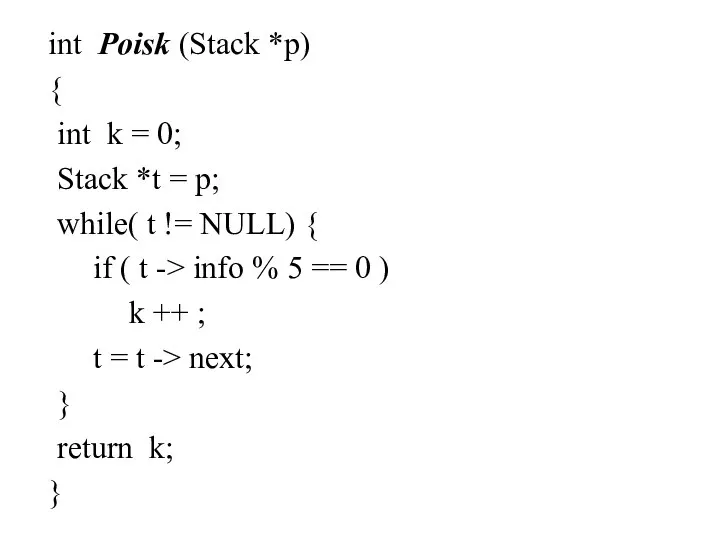
 Переменные. Сложение чисел: простое решение. 10 класс
Переменные. Сложение чисел: простое решение. 10 класс History of the profession System administrator
History of the profession System administrator Устройства современного компьютера
Устройства современного компьютера Антивирусы. Анализ антивирусов
Антивирусы. Анализ антивирусов Знакомство c системой трехмерного твердотельного моделирования
Знакомство c системой трехмерного твердотельного моделирования Как записаться на прием к врачу
Как записаться на прием к врачу Использование возможностей образовательной онлайн платформы Учи.ру
Использование возможностей образовательной онлайн платформы Учи.ру e2cb6cb5560e41b6a04c5e8e6d580639
e2cb6cb5560e41b6a04c5e8e6d580639 Практика. Курсовой проект. Страница интернет магазина
Практика. Курсовой проект. Страница интернет магазина Строки в C#
Строки в C# Информационная безопасность несовершеннолетних в семье
Информационная безопасность несовершеннолетних в семье RFID технология: Открытая библиотека
RFID технология: Открытая библиотека История компьютера
История компьютера Изменения в единицах измерения
Изменения в единицах измерения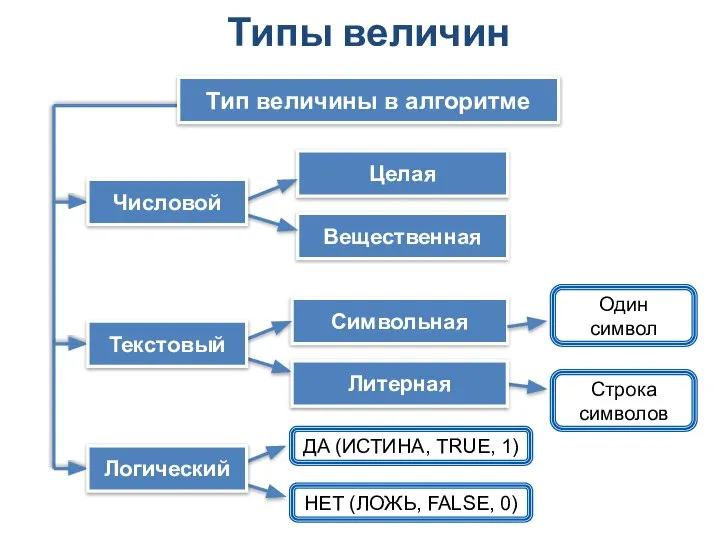 Типы величин. Тип величины в алгоритме
Типы величин. Тип величины в алгоритме Система проведения курсов с автоматизированной проверкой лабораторных работ по программированию
Система проведения курсов с автоматизированной проверкой лабораторных работ по программированию Middlewar server Stalker. Прием телеканалов через сеть Интернет
Middlewar server Stalker. Прием телеканалов через сеть Интернет Конкурс по поиску информации в интернете. Деловая игра
Конкурс по поиску информации в интернете. Деловая игра Алгоритмы и модели трассировки печатных соединений в ЭА
Алгоритмы и модели трассировки печатных соединений в ЭА Инди-игра Color Fall
Инди-игра Color Fall Разработка компьютерной игры
Разработка компьютерной игры Анализ и синтез пакетных сетей по показателям качества
Анализ и синтез пакетных сетей по показателям качества Night Magic Glade. Добро пожаловать
Night Magic Glade. Добро пожаловать Предмет и структура информатики
Предмет и структура информатики Основы языка программирования Java
Основы языка программирования Java Умный город
Умный город JavaScript
JavaScript Области применения табличного процессора
Области применения табличного процессора