Слайд 2Побитовая конъюнкция &
Чтобы определить, чему равна побитовая конъюнкция двух чисел, нужно перевести
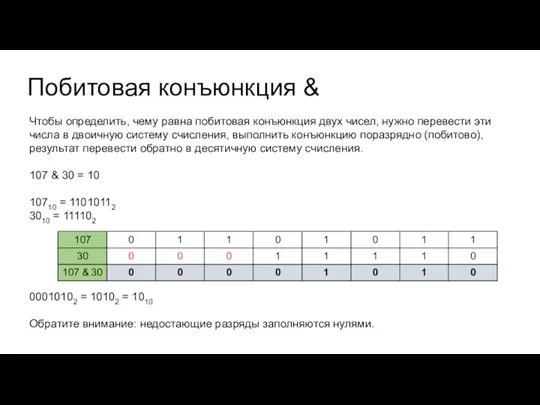
эти числа в двоичную систему счисления, выполнить конъюнкцию поразрядно (побитово), результат перевести обратно в десятичную систему счисления.
107 & 30 = 10
10710 = 11010112
3010 = 111102
00010102 = 10102 = 1010
Обратите внимание: недостающие разряды заполняются нулями.
Слайд 3Сравнение с нулём
Пример 1:
107 & 30 = 10 – в результате побитовой

конъюнкции получилось число 10. Также будет верно, что:
107 & 30 ≠ 0
и
107 & 30 ≠ 11 (или любому другому числу кроме 10)
Пример 2:
107 & 20 = 0 – в результате побитовой конъюнкции получился 0
Также будет верно, что 107 & 20 ≠ 1 (или любому другому числу кроме 0).
Слайд 5Задача 1
Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K

(логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число a, такое что выражение
( x & 125 = 1) → ((x & 34 = 2) → (x & a = 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной x)?
Слайд 6Решение задачи 1
1) упростим:
(x & 125 = 1) → ((x & 34

= 2) → (x & a = 0))
(x & 125 ≠ 1) ∨ ((x & 34 = 2) → (x & a = 0))
(x & 125 ≠ 1) ∨ (x & 34 ≠ 2) v (x & a = 0)
2) разобъём выражение на две части: в первой части содержится буква а, во второй – нет:
первая часть: (x & a = 0)
вторая часть: (x & 125 ≠ 1) ∨ (x & 34 ≠ 2)
Слайд 7Решение задачи 1
3) определим, как выглядит проблемный х: добавим отрицание ко второй

части
¬((x & 125 ≠ 1) ∨ (x & 34 ≠ 2))
¬(x & 125 ≠ 1) ∧ ¬(x & 34 ≠ 2))
(x & 125 = 1) ∧ (x & 34 = 2)
4) Определим, как выглядит х в двоичной системе счисления:
(x & 125 = 1)
12510 = 11111012
Слайд 8Решение задачи 1
Т.к. мы знаем результат конъюнкции, некоторые биты х восстановить можно.
Чему
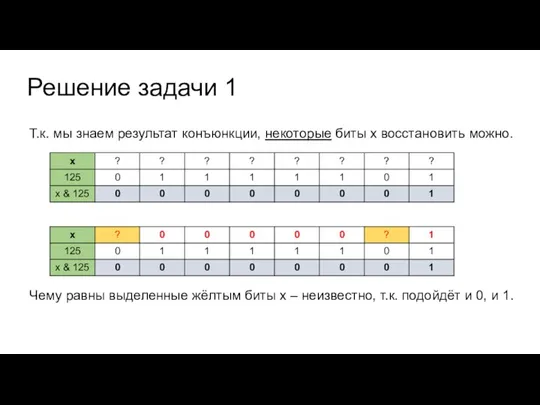
равны выделенные жёлтым биты х – неизвестно, т.к. подойдёт и 0, и 1.
Слайд 9Решение задачи 1
Проделаем то же самое со вторым выражением:
(x & 34 =
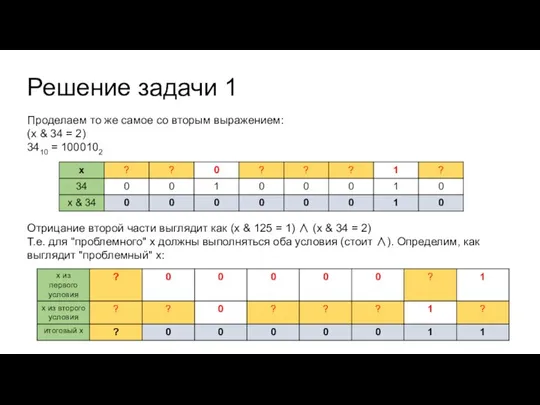
2)
3410 = 1000102
Отрицание второй части выглядит как (x & 125 = 1) ∧ (x & 34 = 2)
Т.е. для "проблемного" х должны выполняться оба условия (стоит ∧). Определим, как выглядит "проблемный" х:
Слайд 10Решение задачи 1
х = 000000112 = 112 = 310
В условии требовалось найти

минимальное натуральное а, при котором исходная формула всегда истинна. Переформулируем: требуется найти минимальное натуральное а, при котором x & a = 0 для "проблемного" х.
Слайд 11Решение задачи 1
Т.к. а должно быть натуральным, придётся хотя бы один бит
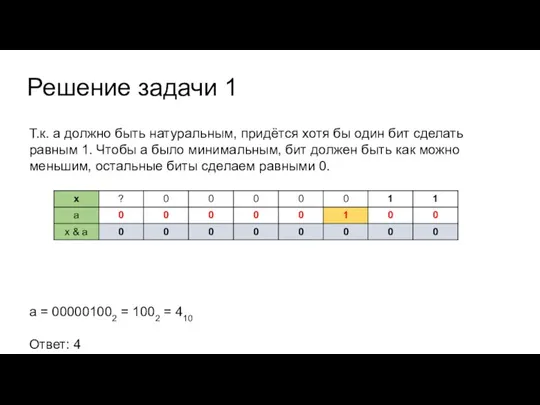
сделать равным 1. Чтобы а было минимальным, бит должен быть как можно меньшим, остальные биты сделаем равными 0.
а = 000001002 = 1002 = 410
Ответ: 4
Слайд 13Самостоятельно
1.1) (X & 35 ≠ 0) → ((X & 31 = 0)

→ (X & A ≠ 0)) – наим. натур. А, тождественно истинно
1.2) (x & 21 = 0) ∨ ( (x & 11 = 0) → (x & A ≠ 0) ) – наим. натур. А, тождественно истинно
1.3) (X & 102 ≠ 0) → ((X & 36 = 0) → (X & A ≠ 0)) – наим. натур. А, тождественно истинно
1.4) Определите наименьшее натуральное число A из интервала [50, 120] такое, что выражение (x & A = 0) → ((x & 31 ≠ 0) → (x & 35 ≠ 0)) тождественно истинно.
Подсказка: вначале решаем задачу обычным способом, при подборе А следим, чтобы число лежало в интервале [50; 120] – как сказано в условии
Слайд 14Ответы
1.1) 32
1.2) 20
1.3) 66
1.4) 60

Слайд 16Задача 2
Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K

(логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число a, такое что выражение
( (x & 28 = 0) → (x & 45 ≠ 0)) → ((x & 48 = 0) → (x & a ≠ 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной x)?
Слайд 17Решение задачи 2
1) упростим:
((x & 28 = 0) → (x & 45

≠ 0)) → ((x & 48 = 0) → (x & a ≠ 0))
((x & 28 ≠ 0) V (x & 45 ≠ 0)) → ((x & 48 = 0) → (x & a ≠ 0))
¬((x & 28 ≠ 0) V (x & 45 ≠ 0)) V ((x & 48 = 0) → (x & a ≠ 0))
¬((x & 28 ≠ 0) V (x & 45 ≠ 0)) V ((x & 48 ≠ 0) V (x & a ≠ 0))
(¬(x & 28 ≠ 0) ∧ ¬(x & 45 ≠ 0)) V (x & 48 ≠ 0) V (x & a ≠ 0)
((x & 28 = 0) ∧ (x & 45 = 0)) V (x & 48 ≠ 0) V (x & a ≠ 0)
2) разобъём выражение на две части: в первой части содержится буква а, во второй – нет:
первая часть: (x & a ≠ 0)
вторая часть: ((x & 28 = 0) ∧ (x & 45 = 0)) V (x & 48 ≠ 0)
Слайд 18Решение задачи 2
3) определим, как выглядит "проблемный" х: добавим отрицание ко второй

части
¬(((x & 28 = 0) ∧ (x & 45 = 0)) V (x & 48 ≠ 0))
¬((x & 28 = 0) ∧ (x & 45 = 0)) ∧ ¬(x & 48 ≠ 0)
(¬(x & 28 = 0) V ¬(x & 45 = 0)) ∧ (x & 48 = 0)
((x & 28 ≠ 0) V (x & 45 ≠ 0)) ∧ (x & 48 = 0)
4) Определим, как выглядит "проблемный" х в двоичной системе счисления:
(x & 28 ≠ 0)
2810 = 111002
Слайд 19Решение задачи 2
Мы не знаем результат конъюнкции, но знаем, что он не
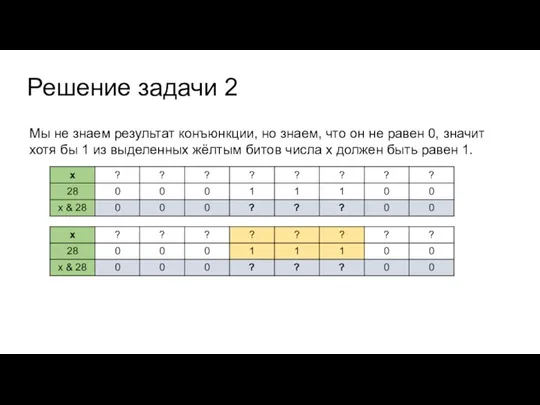
равен 0, значит хотя бы 1 из выделенных жёлтым битов числа х должен быть равен 1.
Слайд 20Решение задачи 2
Проделаем то же самое со вторым выражением:
(x & 45 ≠
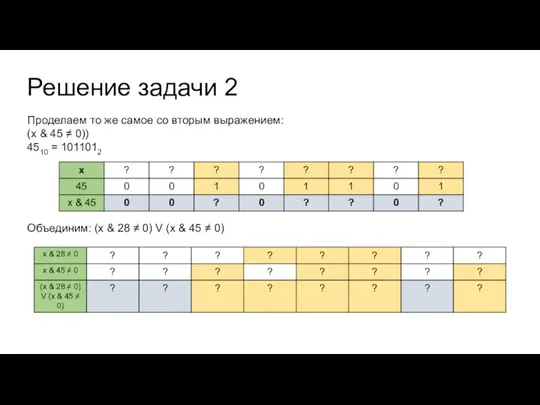
0))
4510 = 1011012
Объединим: (x & 28 ≠ 0) V (x & 45 ≠ 0)
Слайд 21Решение задачи 2
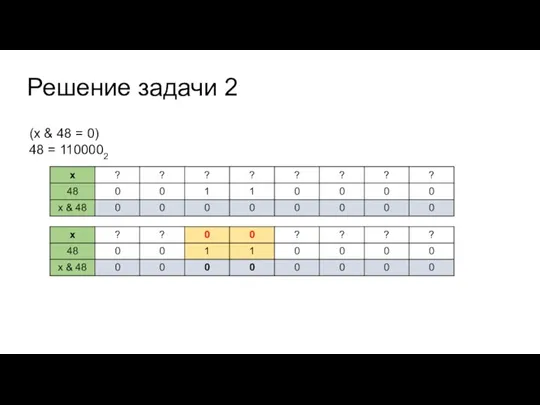
(x & 48 = 0)
48 = 1100002
Слайд 22Решение задачи 2
((x & 28 ≠ 0) V (x & 45 ≠

0)) ∧ (x & 48 = 0)
Обратите внимание: между выражениями стоит конъюнкция.
В итоговом х в любом выделенным жёлтом бите может стоять 1 (и хотя бы одна такая единица есть).
Нужно найти минимальное натуральное а, которое не даст 0 при побитовой конъюнкции с х.
В таблице показан вид любого а, которое не даст 0 при конъюнкции с х, не только минимального.
Слайд 23Решение задачи 2
а будет минимальным, если все биты, помеченные ?, равны 0.
Ответ:
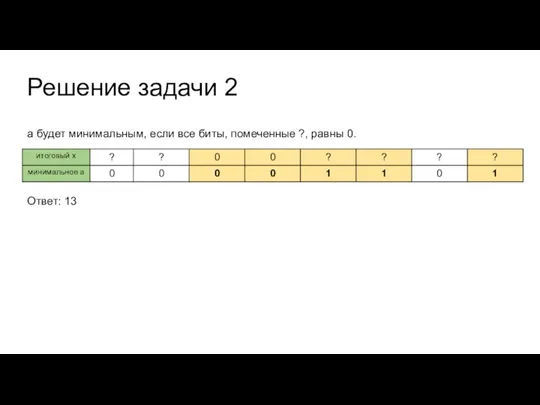
13
Слайд 25Задача 3
Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K

(логическое «И» между соответствующими битами двоичной записи). Определите наибольшее натуральное число a, такое что выражение
(( (x & a ≠ 0) ∧ (x & 12 = 0)) → ((x & a = 0) ∧ (x & 21 ≠ 0))) ∨ ((x & 21 = 0) ∧ (x & 12 = 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Слайд 26Решение задачи 3
1) упростим:
(( (x & a ≠ 0) ∧ (x &

12 = 0)) → ((x & a = 0) ∧ (x & 21 ≠ 0))) ∨ ((x & 21 = 0) ∧ (x & 12 = 0))
(¬( (x & a ≠ 0)∧(x & 12 = 0)) v ((x & a = 0) ∧ (x & 21 ≠ 0))) ∨ ((x & 21 = 0) ∧ (x & 12 = 0))
( (¬(x & a ≠ 0) v ¬(x & 12 = 0)) v ((x & a = 0) ∧ (x & 21 ≠ 0))) ∨ ((x & 21 = 0) ∧ (x & 12 = 0))
((x & a = 0) v (x & 12 ≠ 0)) v ((x & a = 0) ∧ (x & 21 ≠ 0)) ∨ ((x & 21 = 0) ∧ (x & 12 = 0))
удалим (x & a = 0) ∧ (x & 21 ≠ 0)), т.к. уже есть (x & a = 0) по правилу X V XY = X
(x & a = 0) v (x & 12 ≠ 0) ∨ ((x & 21 = 0) ∧ (x & 12 = 0))
2) разобъём выражение на две части: в первой части содержится буква а, во второй – нет:
первая часть: (x & a = 0)
вторая часть: (x & 12 ≠ 0) ∨ ((x & 21 = 0) ∧ (x & 12 = 0))
Слайд 27Решение задачи 3
3) определим, как выглядит "проблемный" х: добавим отрицание ко второй

части
¬((x & 12 ≠ 0) ∨ ((x & 21 = 0) ∧ (x & 12 = 0)))
(¬(x & 12 ≠ 0) ∧ ¬((x & 21 = 0) ∧ (x & 12 = 0)))
((x & 12 = 0) ∧ (¬(x & 21 = 0) V ¬(x & 12 = 0)))
( (x & 12 = 0) ∧ ((x & 21 ≠ 0) V (x & 12 ≠ 0)) )
4) Определим, как выглядит "проблемный" х в двоичной системе счисления:
(x & 12 = 0)
1210 = 11002
Слайд 28Решение задачи 3
(x & 21 ≠ 0)
21 = 101012
На месте хотя бы
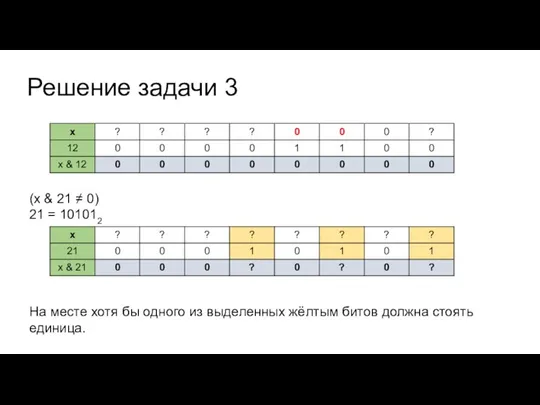
одного из выделенных жёлтым битов должна стоять единица.
Слайд 29Решение задачи 3
(x & 12 ≠ 0)
12 = 11002
На месте хотя бы

одного из выделенных жёлтым битов должна стоять единица.
(x & 21 ≠ 0) V (x & 12 ≠ 0)
Слайд 30Решение задачи 3
(x & 12 = 0) ∧ ((x & 21 ≠

0) V (x & 12 ≠ 0))
Требуется найти такое наибольшее натуральное а, что (x & a = 0).
Слайд 31Решение задачи 3
Требуется найти такое наибольшее натуральное а, что (x & a

= 0).
а = 0000011002 = 11002 = 1210
Ответ: 12
Слайд 33Самостоятельно
4) (x & 10 ≠ 0) ∨ (x & 39 = 0) ∧ (x & 149 = 0) ∨ (x & А = 0) – наим. натур. А,

тождественно истинно
5) (x & 51 ≠ 0) → (x & А ≠ 0) ∨ ¬ ((x & 11 ≠ 0) ∨ (x & А ≠ 0)) – наим. натур. А, тождественно истинно
6) ( (x & 28 = 0) ∨ (x & 22 = 0)) → ((x & 56 ≠ 0) → (x & A = 0)) – наиб. натур. А, тождественно истинно
7) ( (x & 38 = 0) ∨ (x & 57 = 0)) → ((x & 11 ≠ 0) → (x & A = 0)) – наиб. натур. А, тождественно истинно
8) Определите наибольшее натуральное число A из интервала [50, 120] такое, что выражение
(x & A = 0) → ((x & 31 ≠ 0) → (x & 35 ≠ 0)) тождественно истинно?
9) (x & A ≠ 0) ∧ (x & 58 = 0) ∧ (x & 22 = 0) – наим. натур. А, тождественно ложно
Подсказка: если выражение тождественно ложно, то его отрицание – тождественно истинно
10) (x & A = 0) ∧ (x & 58 ≠ 0) ∧ (x & 22 = 0) – наиб. натур. А, тождественно ложно
11) ((x & A ≠ 0) → (x & 62 ≠ 0)) → ((x & 24 = 0) ∧ (x & A ≠ 0)) – наим. натур. А, тождественно ложно
Слайд 34Ответы
4) 2
5) 11
6) 20
7) 32
8) 95
9) 40
10) 62
11) 8


































 Функции объекта. Характеристика объекта по плану
Функции объекта. Характеристика объекта по плану Безопасный Интернет
Безопасный Интернет Лекция №6. Введение в понятие алгоритма. Классификация языков программирования
Лекция №6. Введение в понятие алгоритма. Классификация языков программирования Формы электронной коммерции
Формы электронной коммерции Источники информации в проектной деятельности
Источники информации в проектной деятельности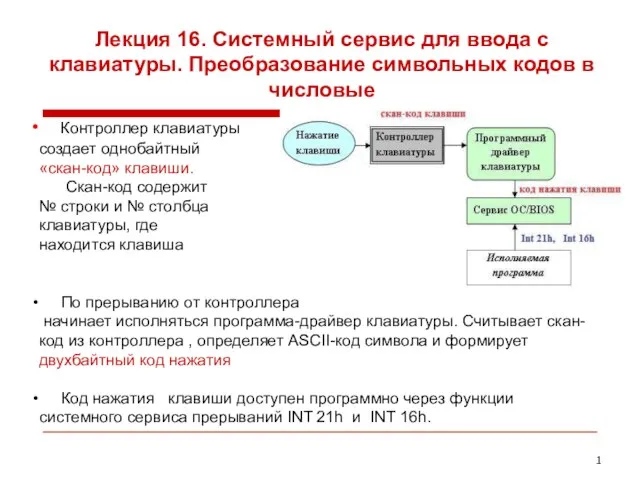 Системный сервис для ввода символов с клавиатуры. Преобразование символьных кодов в числовые. (Лекция 16)
Системный сервис для ввода символов с клавиатуры. Преобразование символьных кодов в числовые. (Лекция 16) ITOtkrytyh_sistem
ITOtkrytyh_sistem База данных SQLite. Лекция 12
База данных SQLite. Лекция 12 Подходы к интеграции программных модулей
Подходы к интеграции программных модулей Разработка сайта для организации хранения и использования проектов студентов
Разработка сайта для организации хранения и использования проектов студентов How dom we use government services
How dom we use government services Комплексный Маркетинг для Вашего Бизнеса. Chat-bot агентство
Комплексный Маркетинг для Вашего Бизнеса. Chat-bot агентство Разработка автоматизированной системы формирования оптимального портфеля заказов предприятия
Разработка автоматизированной системы формирования оптимального портфеля заказов предприятия Анализ поверхности
Анализ поверхности Рекурсивные функции
Рекурсивные функции Типовая структура интерфейса текстовых редакторов
Типовая структура интерфейса текстовых редакторов История Слендермена
История Слендермена Dastriy ta‘minot sifatining analizi. Payme
Dastriy ta‘minot sifatining analizi. Payme Программное обеспечение для обучения основ программирования детей школьного возраста на мобильных устройствах
Программное обеспечение для обучения основ программирования детей школьного возраста на мобильных устройствах Презентация на тему Урок Photoshop
Презентация на тему Урок Photoshop  Интерактивные форматы и особенности вёрстки в медиа
Интерактивные форматы и особенности вёрстки в медиа Безопасная паутина. Урок безопасности в интернете
Безопасная паутина. Урок безопасности в интернете Информационные угрозы. 11 класс
Информационные угрозы. 11 класс Виртуальный 3D тур по школе, г. Бор
Виртуальный 3D тур по школе, г. Бор Информационные технологии комплектации заказов в логистике
Информационные технологии комплектации заказов в логистике 30 сентября - День интернета в России
30 сентября - День интернета в России Запрос на обновление
Запрос на обновление Моделі системи глобальної інформаційної безпеки
Моделі системи глобальної інформаційної безпеки