Содержание
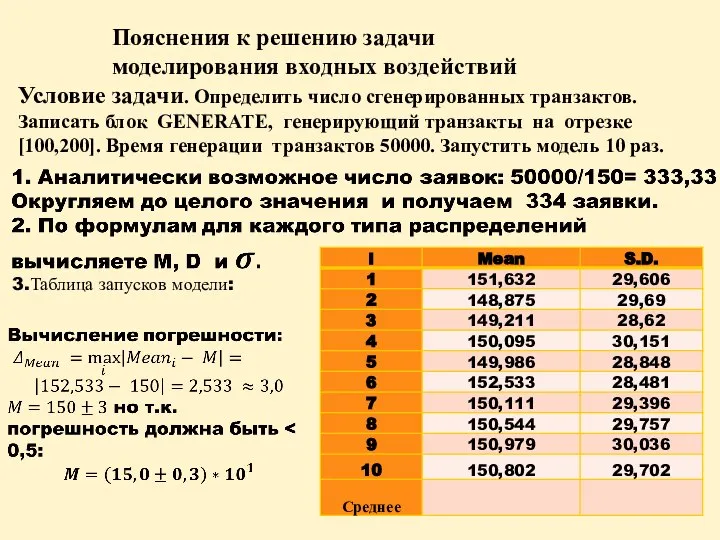
- 2. Пояснения к решению задачи моделирования входных воздействий Условие задачи. Определить число сгенерированных транзактов. Записать блок GENERATE,
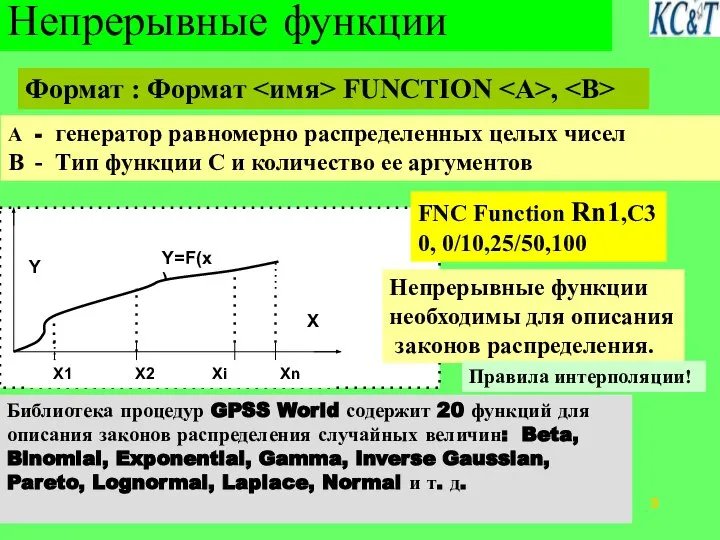
- 3. Непрерывные функции Формат : Формат FUNCTION , A - генератор равномерно распределенных целых чисел B -
- 4. Xpdis FUNCTION RN200,C24 0,0/.1,.104/.2,.222/.3,.355/.4,.509/.5,.69/.6,.915/.7,1.2/.75,1.38 .8,1.6/.84,1.83/.88,2.12/.9,2.3/.92,2.52/.94,2.81/.95,2.99/.96,3.2 .97,3.5/.98,3.9/.99,4.6/.995,5.3/.998,6.2/.999,7/.9998,8 Output FUNCTION V$Input,C3 1.2,10.1/20.1,98.7/33.5,689.2 Метод линейной интерполяции позволяет вычислить значение
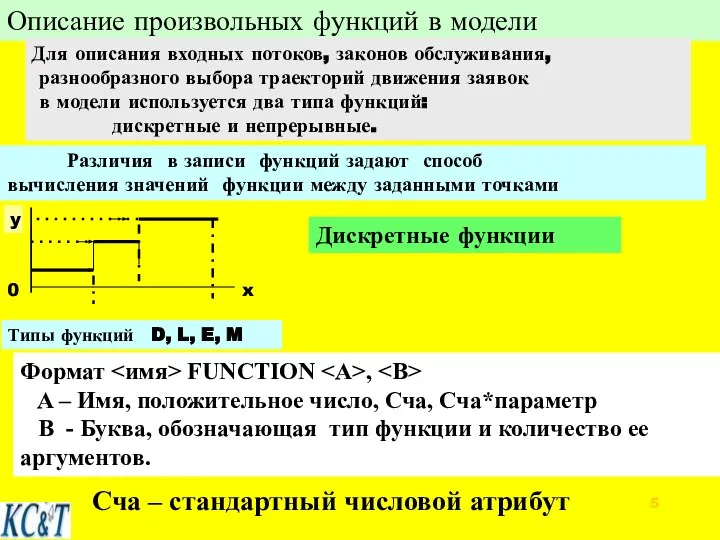
- 5. Описание произвольных функций в модели Для описания входных потоков, законов обслуживания, разнообразного выбора траекторий движения заявок
- 6. FFDD Function RN1,D3 Дискретная числовая функция O.1,10/0.4,15/1,40 Вероятности значений: 0.1, 0.3,0.6 FFDEStation FUNCTION X$QRA,E4 4 Дискретная
- 7. Принцип Парето очень часто встречается в самых разных областях. Например, в том, что 20 % людей
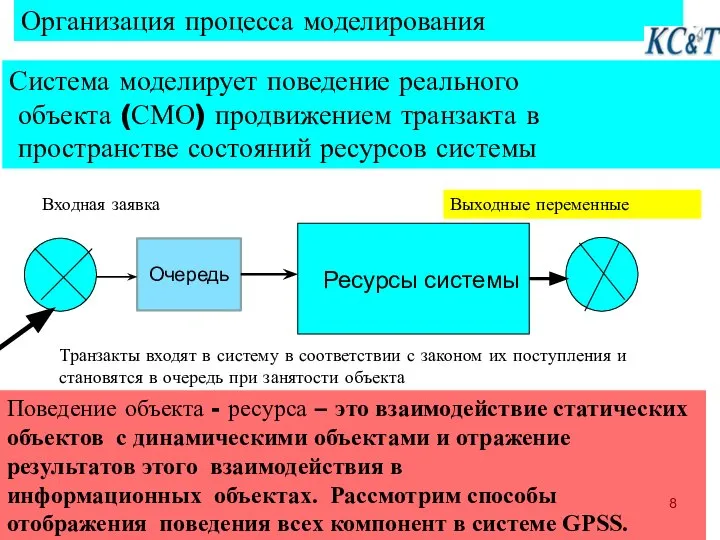
- 8. Организация процесса моделирования Система моделирует поведение реального объекта (СМО) продвижением транзакта в пространстве состояний ресурсов системы
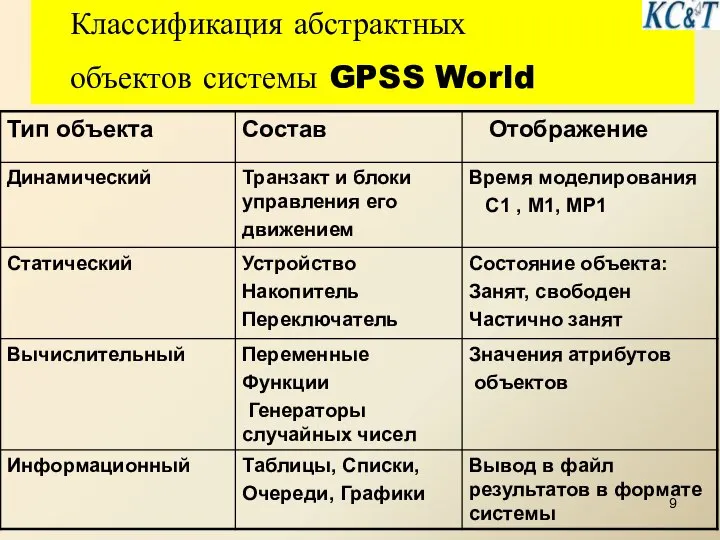
- 9. Классификация абстрактных объектов системы GPSS World
- 10. Устройства (Facilities) Все многообразие ресурсов любой СМО представляется тремя типами устройств SEIZE Занято RELEASE Свободно PREEMPT
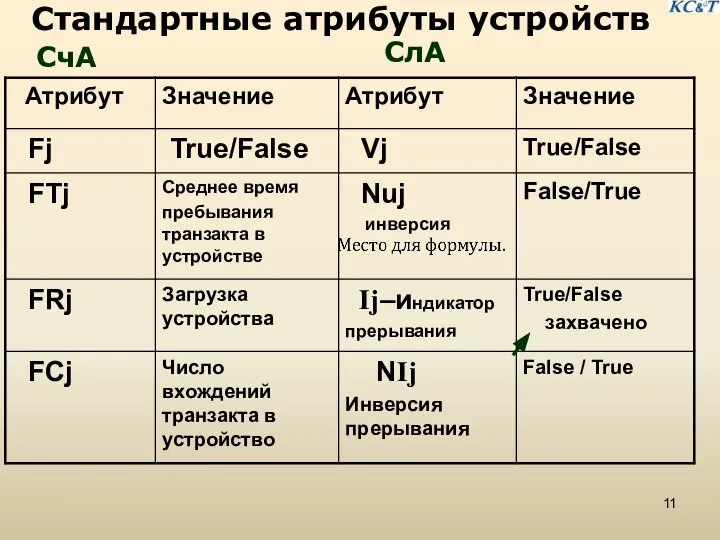
- 11. Стандартные атрибуты устройств СчА СлА
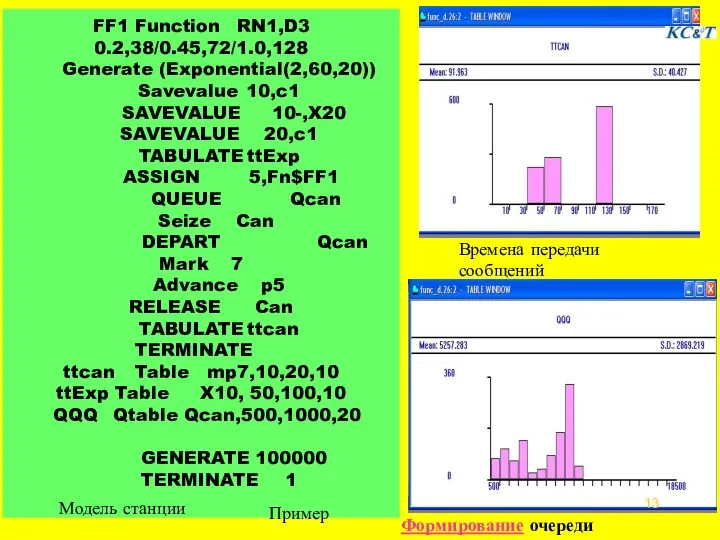
- 12. Пример использования функций и ресурса системы Задача. На рабочую станцию поступают сообщения с трех терминалов. Поток
- 13. FF1 Function RN1,D3 0.2,38/0.45,72/1.0,128 Generate (Exponential(2,60,20)) Savevalue 10,c1 SAVEVALUE 10-,X20 SAVEVALUE 20,c1 TABULATE ttExp ASSIGN 5,Fn$FF1
- 14. Аналитическое определение параметров модели Связь физических характеристик ВС с модельными характеристиками Для определения загрузки устройств или
- 15. Моделирование одноканальной системы Дана СМО с одним входом и одним ресурсом для обслуживания. Время поступления заявок
- 17. Скачать презентацию







 مرحبا بكم يا أطفالي
مرحبا بكم يا أطفالي Диагностика и ремонт печатающей техники
Диагностика и ремонт печатающей техники Создание интернет-площадки
Создание интернет-площадки Создание сервера
Создание сервера Что умеет компьютер
Что умеет компьютер Разветвляющийся алгоритм 6 класс
Разветвляющийся алгоритм 6 класс Алгоритм
Алгоритм Инструкция подачи запроса на получение сертификата с использованием онлайн сервиса
Инструкция подачи запроса на получение сертификата с использованием онлайн сервиса Представление данных. Принципы кодирования информации. Раздел 2
Представление данных. Принципы кодирования информации. Раздел 2 Проектирование информационных систем для управления. Системы счисления
Проектирование информационных систем для управления. Системы счисления Психология программирования
Психология программирования Программирование на языке Паскаль
Программирование на языке Паскаль Создание приложений на С++ с помощью DirectX
Создание приложений на С++ с помощью DirectX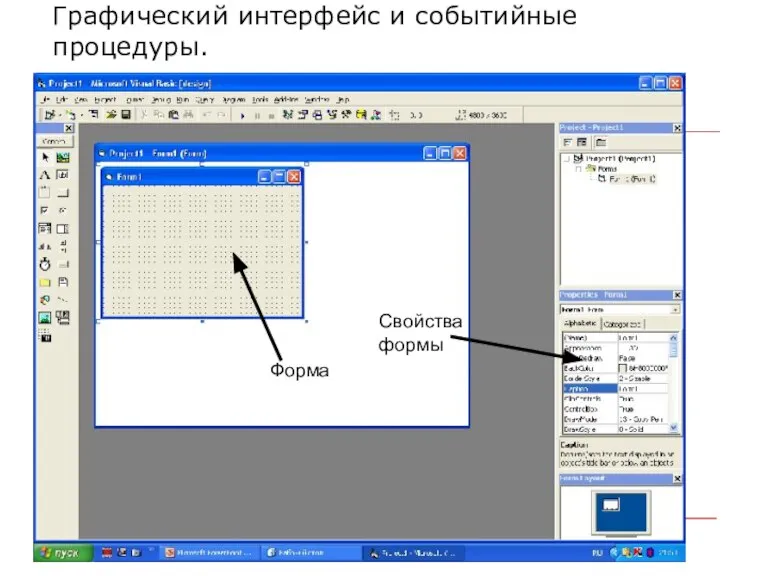 Графический интерфейс и событийные процедуры
Графический интерфейс и событийные процедуры Приём заявлений в 1 класс
Приём заявлений в 1 класс Сложные алгоритмические структуры. Ветвления и циклы
Сложные алгоритмические структуры. Ветвления и циклы Countdown 4 Poster Scheme
Countdown 4 Poster Scheme Лекция 7
Лекция 7 Цветовое решение фильма
Цветовое решение фильма Системы хранения информации. Многоуровневые системы опорных образов (урок 14)
Системы хранения информации. Многоуровневые системы опорных образов (урок 14) Как устроен компьютер. 5 класс
Как устроен компьютер. 5 класс Виды угроз компьютерной информации
Виды угроз компьютерной информации Модульное программирование. Глава 4
Модульное программирование. Глава 4 Шаблоны, экранные формы, слияние в MS Word
Шаблоны, экранные формы, слияние в MS Word Графический редактор
Графический редактор Выровнять поверхность изделия
Выровнять поверхность изделия Презентация на тему Виды носителей информации
Презентация на тему Виды носителей информации  Проектирование автоматизированных систем сбора данных приборов учета
Проектирование автоматизированных систем сбора данных приборов учета