Определения основные понятия свойства множеств. Схема множеств

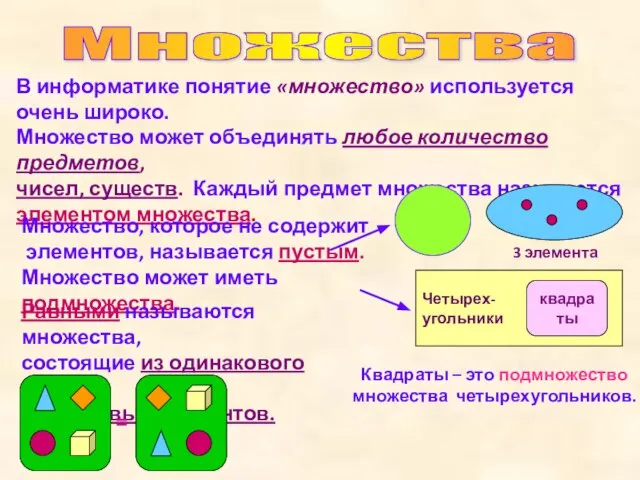
Множества
В информатике понятие «множество» используется очень широко.
Множество может объединять любое количество предметов,
чисел, существ. Каждый предмет множества называется
элементом множества.
Множество, которое не содержит
элементов, называется пустым.
Множество может иметь подмножества.
Равными называются множества,
состоящие из одинакового числа
одинаковых элементов.
Квадраты – это подмножество
множества четырехугольников.

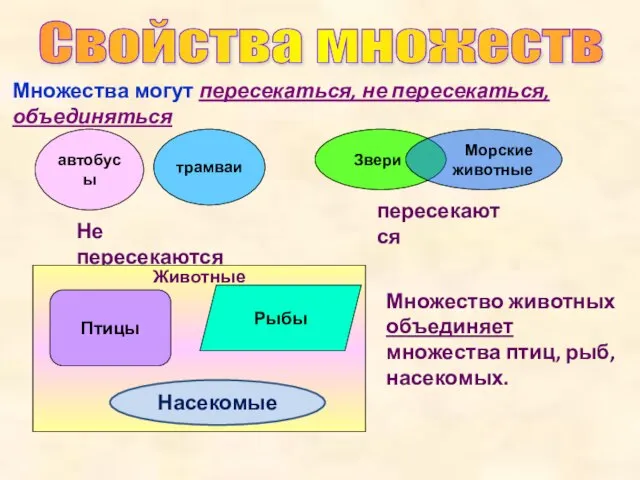
Свойства множеств
Множества могут пересекаться, не пересекаться, объединяться
автобусы
трамваи
Не пересекаются
Звери
Морские
животные
пересекаются
Множество животных
объединяет множества птиц, рыб, насекомых.

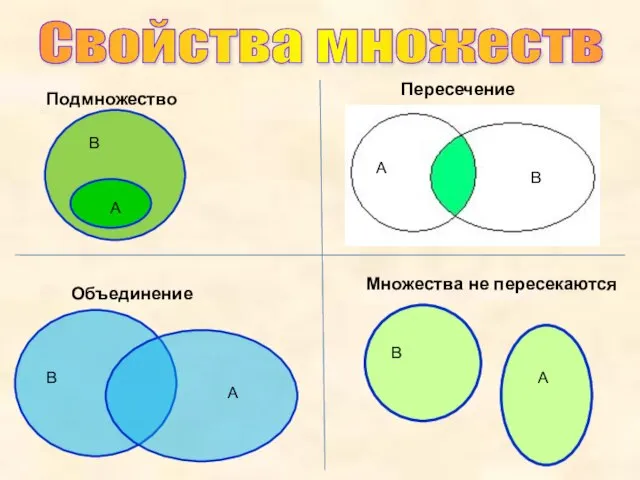
Подмножество
Пересечение
Объединение
Множества не пересекаются
Свойства множеств

В названиях множеств могут употребляться слова
«и», «не», «или», «не … и», «не … или»
Если в названии множества есть слово «не»,
то его элементы находятся за пределами фигуры,
обозначающей это множество.
Если в названии множества есть слово «и»,
то его элементы находятся на пересечении фигур,
обозначающих множества.
Если в названии множества есть слово «или»,
то это означает, что его элементы находятся
в нескольких фигурах.
НЕ
ИЛИ
И
отрицание
пересечение
объединение

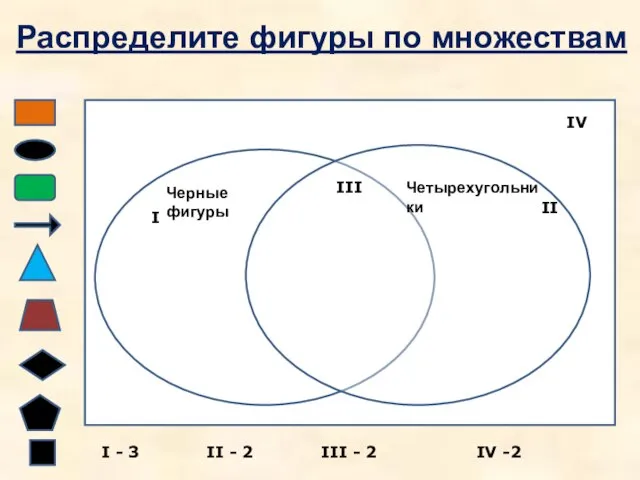
Черные фигуры
Четырехугольники
I
II
III
IV
Распределите фигуры по множествам
I - 3
II - 2
III - 2
IV -2

Задача 1. В одной деревне живут 40 жителей. 12 из них имеют коз, 28 имеют коров, а 5 не имеют ни коз, ни коров. Имеет ли кто-то из жителей деревни сразу и коз и коров?
Задача 2. В киоске около школы продается мороженое двух видов: «Спортивное» и «Мальвина». На перемене 24 ученика успели купить мороженое. При этом 15 из них купили «Спортивное», а 17 – мороженое «Мальвина». Сколько человек купили мороженое обоих сортов?
Задача 3. 12 учащихся класса любят детектив, 18 – фантастику, 3 и то и другое, 1 ничего не читает. Сколько человек в классе?
ЗАДАЧИ

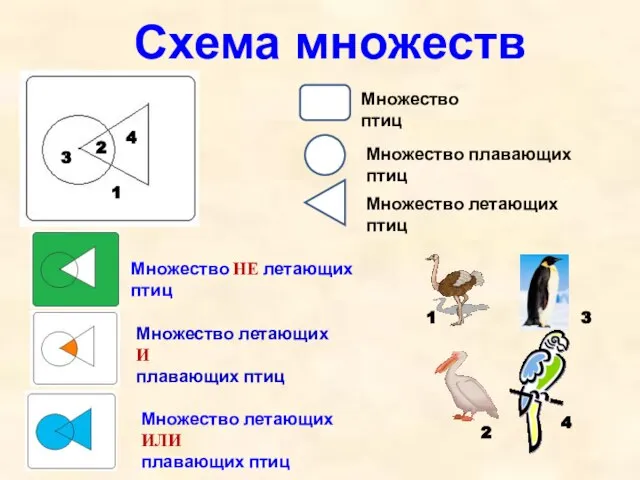
Схема множеств
Множество птиц
Множество плавающих птиц
Множество летающих птиц
Множество НЕ летающих птиц
Множество летающих И
плавающих птиц
Множество летающих ИЛИ
плавающих птиц
1
2
3
4
4
2
1
3

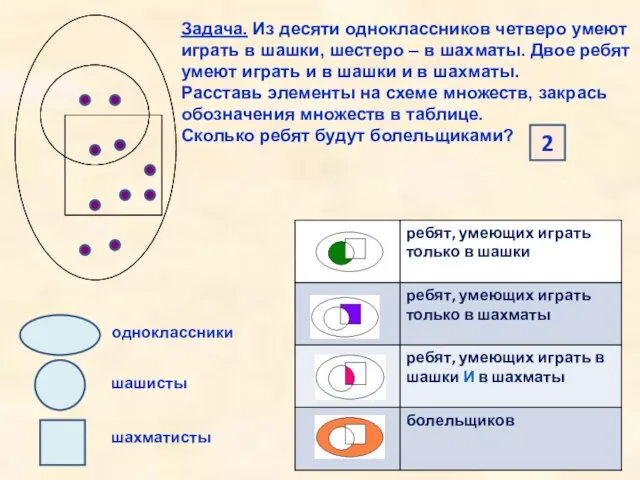
Задача. Из десяти одноклассников четверо умеют играть в шашки, шестеро – в шахматы. Двое ребят умеют играть и в шашки и в шахматы.
Расставь элементы на схеме множеств, закрась обозначения множеств в таблице.
Сколько ребят будут болельщиками?
2
одноклассники
шахматисты
шашисты

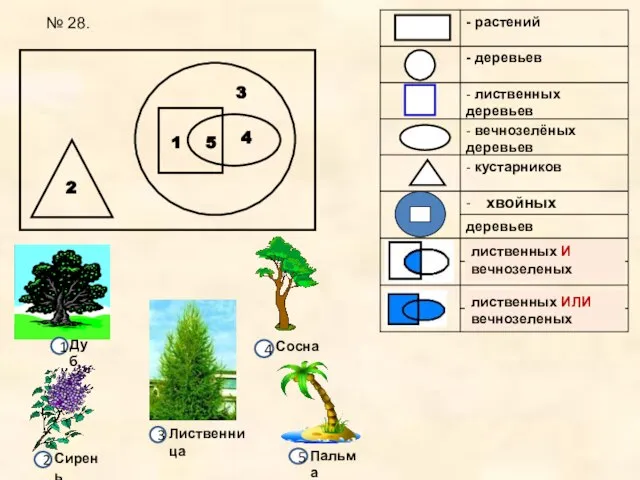
1
2
3
4
5
хвойных
лиственных И вечнозеленых
лиственных ИЛИ вечнозеленых
№ 28.

Высказывания
Предложения «Буква М – согласная» и «6 меньше, чем 9» верные.
Предложения «Луна – спутник Марса» и «Дважды два равно 9» - неверные.
Но есть такие предложения, которые не являются ни верными, ни неверными.
Например, «Который час?», «Войдите!» - высказываниями не являются.
Предложение «В нашем классе а учеников» содержит переменную а.
При подстановке вместо а различных значений получаются верные и
неверные высказывания, их называют высказываниями с переменной.
Высказывание – это утверждение, про которое можно сказать верное оно (истинное) или неверное (ложное).
Значение высказывания «Истина» принято обозначать словом «да»
или цифрой 1, а значение «Ложь» - словом «нет» или цифрой 0.

Высказывания с логическими
словами «И», «ИЛИ», «НЕ»
Высказывание со словом «не» истинно тогда, когда такое же высказывание без слова «не» ложно, и наоборот.
Высказывание со словом «и» состоит из двух высказываний и истинно тогда, когда истинны оба высказывания.
Высказывание со словом «или» тоже состоит из двух высказываний, но оно истинно тогда, когда истинна хотя бы одна «половина».

сосна, лиственница
Дерево лиственное
ИЛИ вечнозеленое
дуб
Дерево НЕ вечнозелёное И НЕ лиственное
ПАЛЬМА

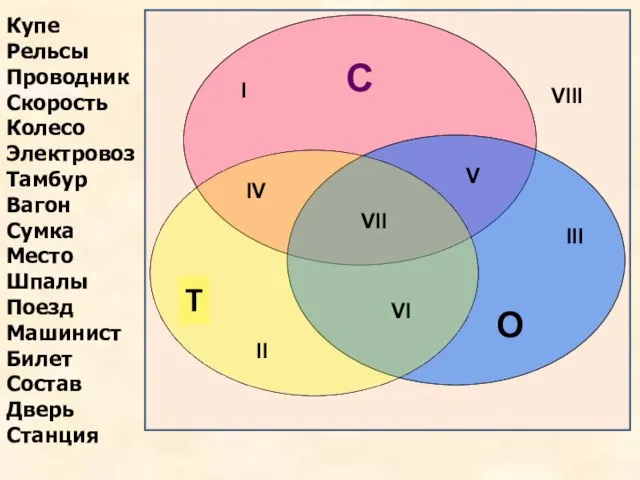
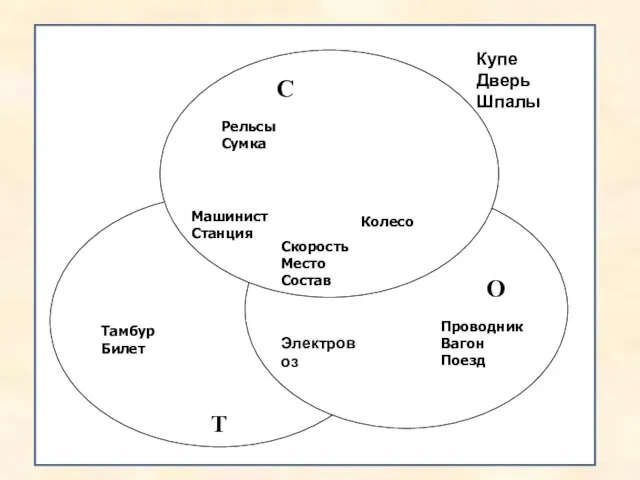
С
О
Купе
Рельсы
Проводник
Скорость
Колесо
Электровоз
Тамбур
Вагон
Сумка
Место
Шпалы
Поезд
Машинист
Билет
Состав
Дверь
Станция
I
II
III
IV
V
VI
VII
VIII

Рельсы
Сумка
Тамбур
Билет
Машинист
Станция
Скорость
Место
Состав
Колесо
Проводник
Вагон
Поезд
Электровоз
Купе
Дверь
Шпалы
О
Т
С

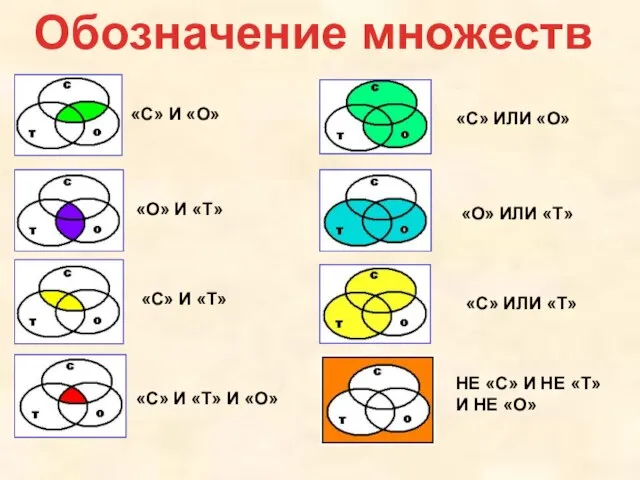
«С» ИЛИ «О»
«О» ИЛИ «Т»
«С» ИЛИ «Т»
НЕ «С» И НЕ «Т»
И НЕ «О»
«С» И «О»
«О» И «Т»
«С» И «Т»
«С» И «Т» И «О»
Обозначение множеств