Компьютерная арифметика. Хранение в памяти целых чисел

Целые числа
.

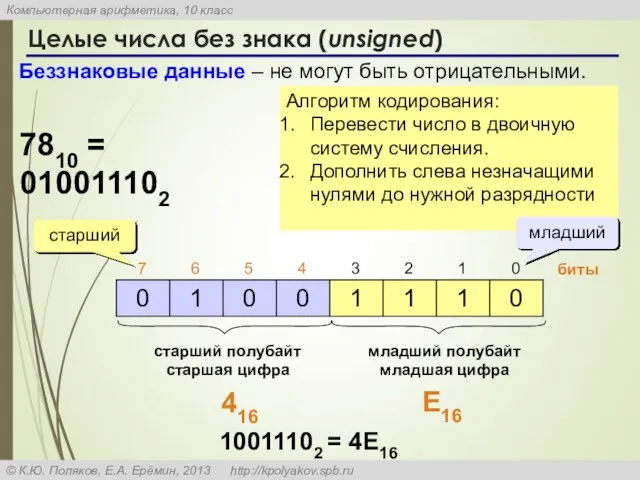
Алгоритм кодирования:
Перевести число в двоичную систему счисления.
Дополнить слева незначащими нулями до нужной разрядности
Целые числа без знака (unsigned)
7810 = 010011102
Беззнаковые данные – не могут быть отрицательными.
10011102 = 4E16

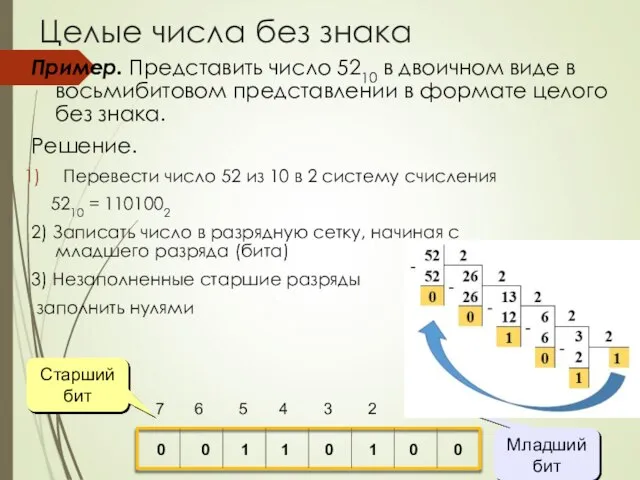
Пример. Представить число 5210 в двоичном виде в восьмибитовом представлении в формате целого без знака.
Решение.
Перевести число 52 из 10 в 2 систему счисления
5210 = 1101002
2) Записать число в разрядную сетку, начиная с
младшего разряда (бита)
3) Незаполненные старшие разряды
заполнить нулями
Целые числа без знака
7 6 5 4 3 2 1 0
Старший бит
Младший бит

Пример. Представить число 5210 в двоичном виде в 16-разрядном представлении в формате целого без знака.
Решение.
Перевести число 52 из 10 в 2 систему счисления
5210 = 1101002
2) Записать число в разрядную сетку, начиная с младшего разряда (бита)
3) Незаполненные старшие разряды заполнить нулями
Целые числа без знака
Старший разряд
Младший разряд

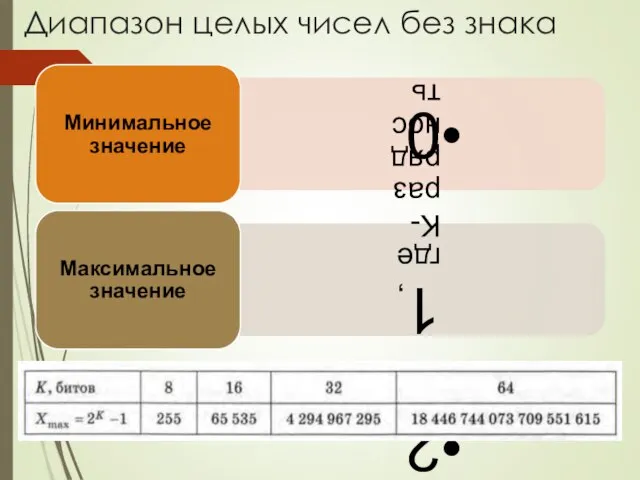
Диапазон целых чисел без знака

Отбросим несуществующий разряд. Получим
255+1=0
При К разрядах арифметика выполняется по модулю 2К, т.е при К = 8
(255+1) mod 256 =
256 mod 256=0
Целые числа без знака
Что будет, если увеличить максимальное число в К-битной ячейке на 1? Пусть К=8, добавим единицу к числу 25510
25510 = 1111 1111 2
110 = 0000 0001 2
1 0000 0000 2
Что получим, вычитая 1 из минимального значения 0?
Ответ: 25510
Факт переполнения фиксируется процессором, нот выполнение программы не прерывается
!

Прямой код – это представление числа в двоичной системе счисления, при этом первый разряд отводится под знак числа.
Старший (знаковый) бит числа определяет его знак. Если он равен 0, число положительное,
если 1, число отрицательное.
Целые числа со знаком
78 = 10011102
– 78 = –10011102
≥ 0
< 0

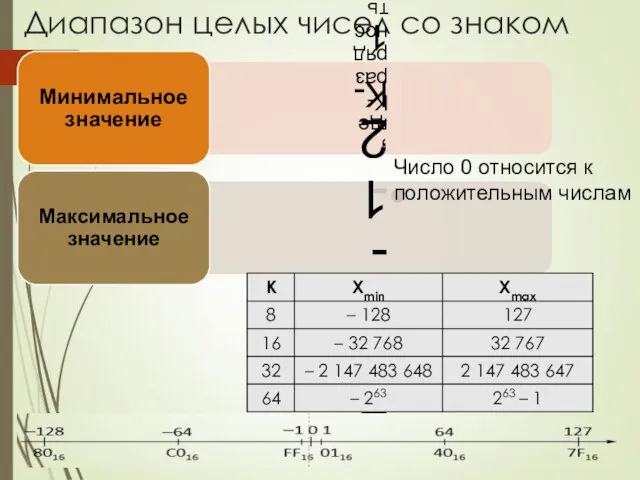
Диапазон целых чисел со знаком
Число 0 относится к положительным числам

5210 = 1101002
- 5210 = - 1101002
Обратный код для положительного числа в двоичной системе счисления совпадает с прямым кодом.
Обратный код для отрицательного числа все цифры положительного числа заменяются на противоположные (1 на 0, 0 на 1).
Прямой код
Обратный код
Прямой код
Обратный код
Целые числа со знаком

Кольцо для целых чисел со знаком для К=8
Граничных значений два: 127 и -128
127+1=?
Выполните проверку самостоятельно, используя образец слайда 7

Хранение целых чисел