Слайд 2 Логическая операция – способ построения сложного высказывания из данных высказываний, при

котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.
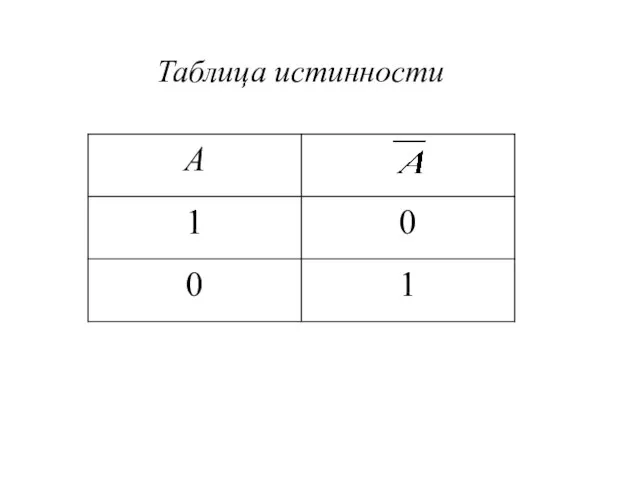
Слайд 3Инверсия (логическое отрицание)
Инверсия логической переменной истина, если переменная ложна, и, наоборот,

инверсия ложна, если переменная истинна.
Обозначение:
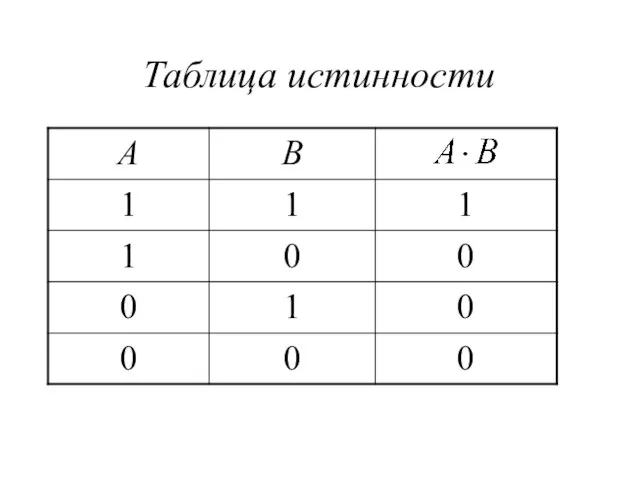
Слайд 5Конъюнкция (логическое умножение)
Конъюнкция двух логических переменных истинна тогда и только

тогда, когда оба высказывания, истинны.
Обозначение:
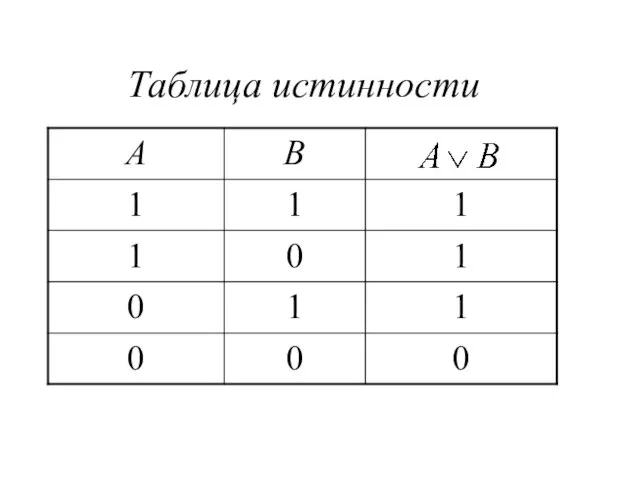
Слайд 7 Дизъюнкция (логическое
сложение)
Дизъюнкция двух логических переменных ложна тогда и

только тогда, когда оба высказывания ложны.
Обозначение:
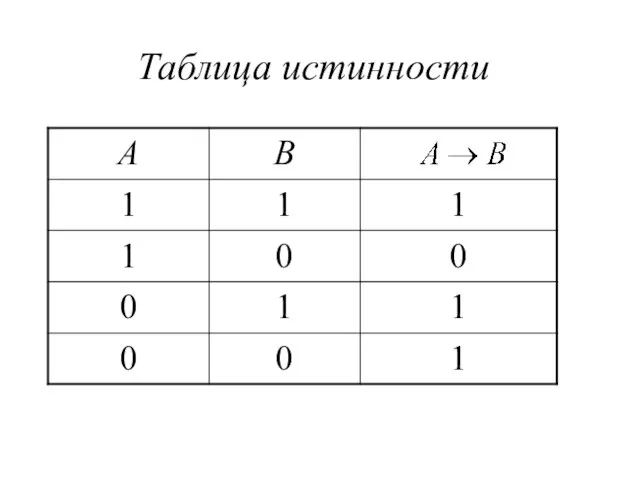
Слайд 9Импликация (логическое следование)
Импликация двух логических переменных ложна тогда и только тогда,

когда из истинного основания следует ложное следствие.
Обозначение:
А - условие
В - следствие
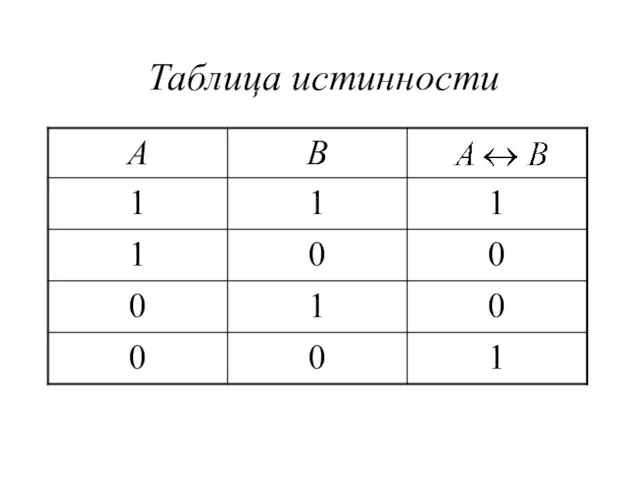
Слайд 11 Эквивалентность (логическое равенство)
Эквивалентность двух логических переменных истинна тогда и

только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
Обозначение:
Слайд 13Приоритет выполнения логических операций
При вычислении значения логического выражения (формулы) логические операции

вычисляются в определенном порядке, согласно их приоритету:
1.инверсия,
2.конъюнкция,
3.дизъюнкция,
4.импликация и эквивалентность.
Операции одного приоритета выполняются слева направо. Для изменения порядка действий используются скобки.
Пример







 Юные блогеры
Юные блогеры Какие эмоции сделают контент вирусным
Какие эмоции сделают контент вирусным Предшественница ЭВМ-аналитическая машина
Предшественница ЭВМ-аналитическая машина Программы для ЭВМ
Программы для ЭВМ Основы построения и функционирования
Основы построения и функционирования Что мы знаем о компьютере (3 класс)
Что мы знаем о компьютере (3 класс) Динамічні КМ БПКС (комутатори з просторовим розподілом)
Динамічні КМ БПКС (комутатори з просторовим розподілом) Настройка программ
Настройка программ Киберпреступность
Киберпреступность Соблюдение требований к вопросам анкеты (на примере исследований Изучение общественного мнения о деятельности местных СМИ)
Соблюдение требований к вопросам анкеты (на примере исследований Изучение общественного мнения о деятельности местных СМИ) ВКР: Проектирование и администрирование сети бизнес отделов интернет..
ВКР: Проектирование и администрирование сети бизнес отделов интернет.. Представление информации в форме таблиц
Представление информации в форме таблиц История внедрения и перспективы практического применения компьютерных технологий при техническом обслуживании
История внедрения и перспективы практического применения компьютерных технологий при техническом обслуживании Помехоустойчивое кодирование
Помехоустойчивое кодирование Фонд развития Интернета
Фонд развития Интернета Технология производства программных продуктов и услуг. Детальное проектирование программ
Технология производства программных продуктов и услуг. Детальное проектирование программ Понятие алгоритма
Понятие алгоритма Lehrmaterialien mit Selbstkorrektur
Lehrmaterialien mit Selbstkorrektur Презентация на тему Архивация данных
Презентация на тему Архивация данных  Короли игровой индустрии
Короли игровой индустрии Базовые конструкции структурного программирования
Базовые конструкции структурного программирования Интерьер. Дизайнеры
Интерьер. Дизайнеры Отсортированная матрица
Отсортированная матрица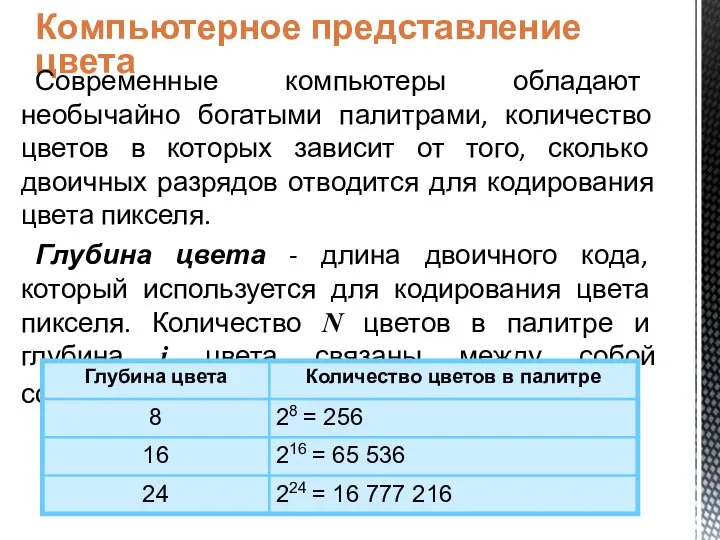 Компьютерное представление цвета
Компьютерное представление цвета Основы алгоритмизации и программирования. Обобщающее повторение
Основы алгоритмизации и программирования. Обобщающее повторение ☻♥ Компьютер и дети ☻♥ Очень много детей, в том числе и взрослые портят зрение из за компьютера!!!
☻♥ Компьютер и дети ☻♥ Очень много детей, в том числе и взрослые портят зрение из за компьютера!!! Воздушно-космическая деятельность
Воздушно-космическая деятельность Основы программирования (на языке Си). Массивы
Основы программирования (на языке Си). Массивы