Основы реляционной алгебры

Реляционная алгебра и СУБД
Доступ к реляционным данным осуществляется при помощи реляционной алгебры.
В реализациях конкретных реляционных СУБД сейчас не используется в чистом виде ни реляционная алгебра, ни реляционное исчисление. Фактическим стандартом доступа к реляционным данным стал язык SQL (Structured Query Language)

Язык SQL представляет собой смесь операторов реляционной алгебры и выражений реляционного исчисления, использующий синтаксис, близкий к фразам английского языка и расширенный дополнительными возможностями, отсутствующими в реляционной алгебре и реляционном исчислении.
Вообще, язык доступа к данным называется реляционно-полным, если он по выразительной силе не уступает реляционной алгебре, т.е. любой оператор реляционной алгебры может быть выражен средствами этого языка. Именно таким и является язык SQL.
Реляционная алгебра и язык SQL

С точки зрения внешнего представления объектов реального мира модель данных — это основные понятия и способы, используемые при анализе и описании предметной области.
Среди многих попыток представить обработку данных на формальном абстрактном уровне реляционная модель, предложенная Э. Ф. Коддом, стала по существу первой работоспособной моделью данных, поскольку помимо средств описания объектов имела эффективный инструментарий преобразований этих описаний — операции реляционной алгебры.
Операции реляционной алгебры

Практически все операторы реляционной модели предназначены для организации запросов к БД в терминах отношений. Эти запросы относятся к включению, соединению, выборке кортежей соответствующих отношений. Традиционно определяют восемь реляционных операторов, объединенных в две группы.
Операторы реляционной алгебры

Теоретико-множественные операторы:
• Объединение
• Пересечение
• Вычитание
• Декартово произведение
Специальные реляционные операторы:
• Выборка
• Проекция • Соединение
• Деление
Операторы реляционной алгебры

Не все они являются независимыми, т.е. некоторые из этих операторов могут быть выражены через другие реляционные операторы.

Отношения, совместимые по типу
Некоторые реляционные операторы (например, объединение) требуют, чтобы отношения имели одинаковые заголовки. Действительно, отношения состоят из заголовка и тела. Операция объединения двух отношений есть просто объединение двух множеств кортежей, взятых из тел соответствующих отношений. Но будет ли результат отношением?

Во-первых, если исходные отношения имеют разное количество атрибутов, то, очевидно, что множество, являющееся объединением таких разнотипных кортежей нельзя представить в виде отношения.
Во-вторых, пусть даже отношения имеют одинаковое количество атрибутов, но атрибуты имеют различные наименования. Как тогда определить заголовок отношения, полученного в результате объединения множеств кортежей?
Отношения, совместимые по типу

В-третьих, пусть отношения имеют одинаковое количество атрибутов, атрибуты имеют одинаковые наименования, но определенны на различных доменах. Тогда снова объединение кортежей не будет образовывать отношение.
Отношения, совместимые по типу

Определение. Будем называть отношения совместимыми по типу, если они имеют идентичные заголовки, а именно:
1. Отношения имеют одно и то же множество имен атрибутов, т.е. для любого атрибута в одном отношении найдется атрибут с таким же наименованием в другом отношении.
2. Атрибуты с одинаковыми именами определены на одних и тех же доменах (или типах, если домены не поддерживаются).

Некоторые отношения не являются совместимыми по типу, но после переименования атрибутов могут ими стать, для этого можно использовать вспомогательный оператор переименования атрибутов.
Отношения, не совместимые по типу

Теоретико-множественные операторы
Объединением двух совместимых по типу отношений А и В называется отношение с тем же заголовком, что и у отношений А и В, и телом, состоящим из совокупности кортежей обоих отношений.
Синтаксис операции:
A UNION B
1

Замечание. Объединение, как и любое отношение, не может содержать одинаковых кортежей. Поэтому, если некоторый кортеж входит и в отношение А, и отношение В, то в объединение он входит один раз.
Теоретико-множественные операторы

Объединение
А
B

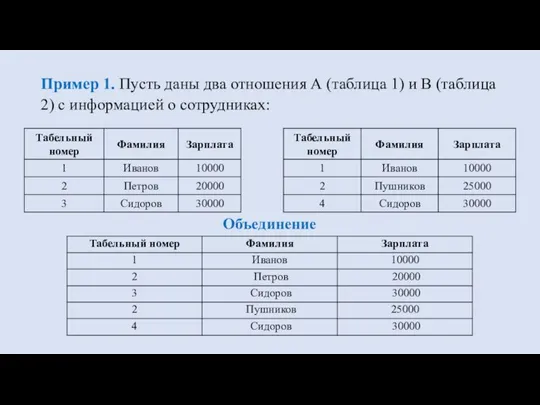
Пример 1. Пусть даны два отношения А (таблица 1) и В (таблица 2) с информацией о сотрудниках:
Объединение

Пересечением двух совместимых по типу отношений А и В называется отношение с тем же заголовком, что и у отношений А и В, и телом, состоящим из кортежей, принадлежащих одновременно обоим отношениям.
Синтаксис операции:
A INTERSECT B
Теоретико-множественные операторы
2

Пересечение
А
B

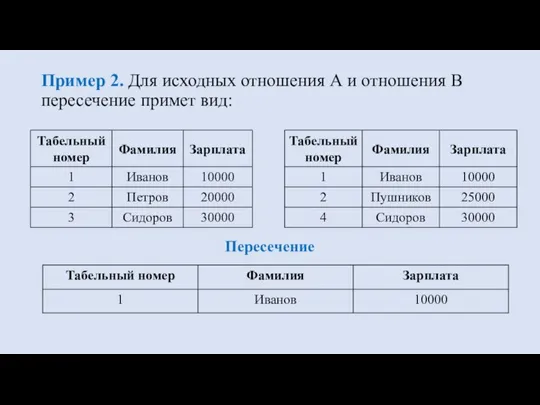
Пример 2. Для исходных отношения А и отношения В пересечение примет вид:
Пересечение

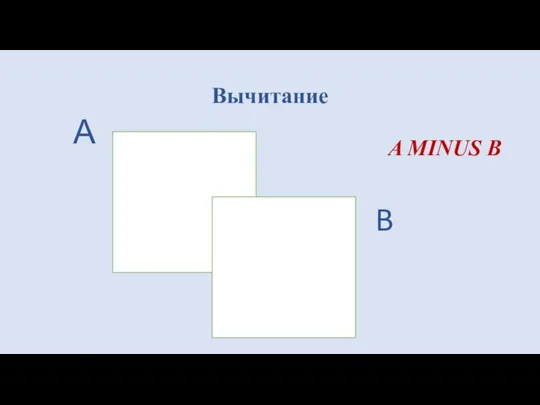
Вычитанием двух совместимых по типу отношений А и В называется отношение с тем же заголовком, что и у отношений А и В, и телом, состоящим из кортежей, принадлежащих отношению А и не принадлежащих отношению В.
Синтаксис операции: A MINUS B
Теоретико-множественные операторы
3

Вычитание
А
B
A MINUS B

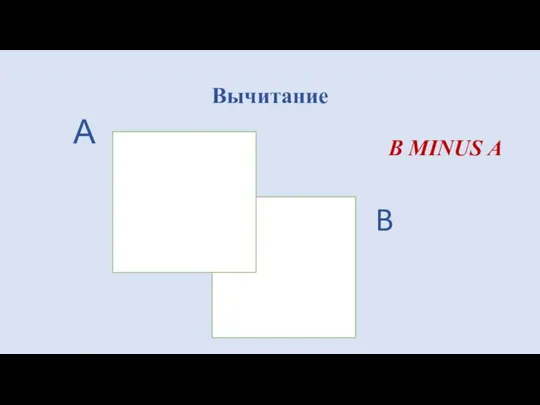
Вычитание
А
B
В MINUS А

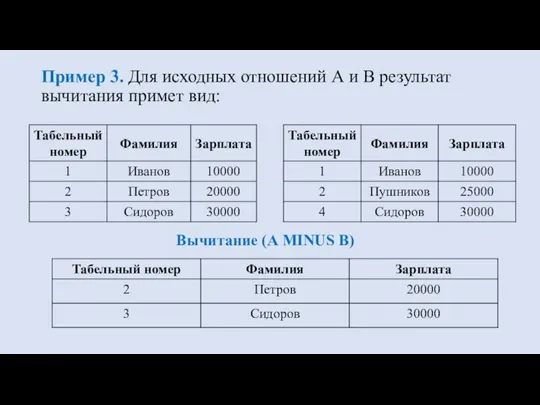
Пример 3. Для исходных отношений А и В результат вычитания примет вид:
Вычитание (А MINUS B)

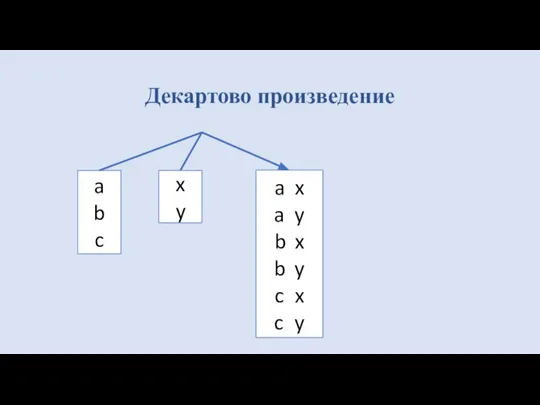
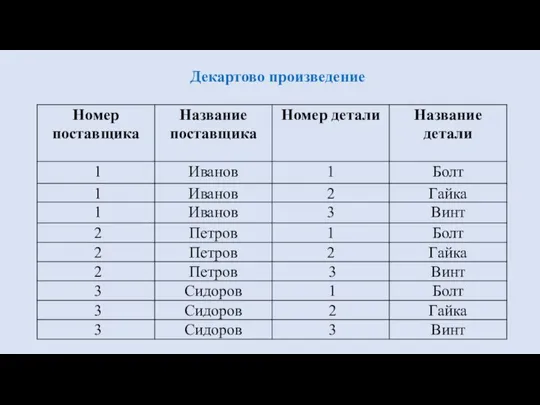
Декартовым произведением двух отношений А и В называется отношение С, полученное сцеплением их заголовков и кортежей соответствующих отношений, причем каждому кортежу отношения А должны быть противопоставлены все кортежи отношения В.
Синтаксис операции: A TIMES B
Теоретико-множественные операторы
4

Декартово произведение

Пример 4. Пусть даны два отношения C и D с информацией о поставщиках и деталях.

Декартово произведение

Замечания:
1. Мощность произведения A TIMES B равна произведению мощностей отношений А и В, т.к. каждый кортеж отношения А соединяется с каждым кортежем отношения В.
2. Если в отношениях А и В имеются атрибуты с одинаковыми именами, то перед выполнением операции такие атрибуты необходимо переименовать.
Теоретико-множественные операторы

3. Перемножать можно любые два отношения, совместимость по типу при этом не требуется.
4. Декартово произведение не дает никакой новой информации, по сравнению с предыдущими операциями, однако она важна для выполнения специальных реляционных операций.

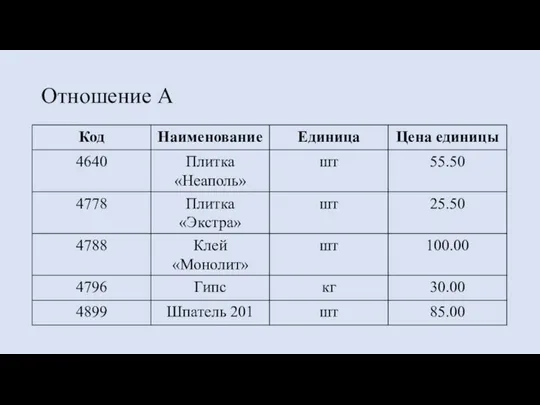
Задание 1.
Даны два отношения А и В, содержащие данные о товарах, необходимо выполнить операции объединения, пересечения и вычитания. Попытайтесь определить смысл результирующих отношений.
Задания для самостоятельной работы

Отношение А

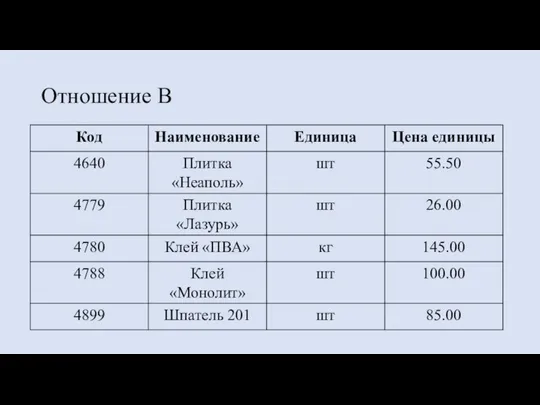
Отношение В

Задание 2. Необходимо ответить на вопросы
Какие отношения называются совместимыми по типу?
В чем смысл реляционного оператора «Объединение»?
В чем смысл реляционного оператора «Пересечение»?
В чем смысл реляционного оператора «Вычитание»?
Почему невозможно использование операций «Объединения», «Пересечения» и «Вычитания», если исходные отношения не совместимы по типу?
В чем смысл реляционного оператора «Декартово произведение»?
Чему равна мощность декартова произведения?

С практической точки зрения, специальные реляционные операции имеют большее практическое значение по сравнению с теоретико-множественными.
Специальные реляционные операторы

Выборкой (ограничением, селекцией или фильтрацией)
на отношении А с условием С называется отношение с тем же заголовком, что и у отношения А, и телом, состоящим из кортежей, значения атрибутов которых при подстановке в условие С дают значение ИСТИНА.
Синтаксис операции:
A WHERE C
С - логическое выражение, в которое могут входить атрибуты отношения А и (или) скалярные выражения.
Специальные реляционные операторы
1

В простейшем случае условие С имеет вид ХΘY, где - Θ один из операторов сравнения (=, ≠, <, >, ≤, ≥ и т.д.), а Х и Y – атрибуты отношения А или скалярные значения. Такие выборки называются Θ - выборки (тэта-выборки) или Θ - селекция, Θ - ограничения.
Выборка

Смысл операции выборки очевиден - выбрать кортежи отношения, удовлетворяющие некоторому условию.
Таким образом, операция выборки дает «горизонтальный срез» отношения по некоторому условию
Выборка

Пример 5. Пусть дано отношение А с информацией о сотрудниках, необходимо выбрать всех сотрудников с зарплатой менее 30000.
А WHERE Зарплата < 30000

Проекцией отношения А по атрибутам X,Y,…, Z,
где каждый из атрибутов принадлежит отношению А,
называется отношение с заголовком (X,Y,…,Z) и телом, содержащим кортежи соответствующих атрибутов.
Синтаксис операции:
А[X,Y,…,Z]
Специальные реляционные операторы
2

Операция проекции дает "вертикальный срез" отношения, в котором удалены все возникшие при таком срезе дубликаты кортежей.
Проекция

Пример 6. Дано отношение А
А [Фамилия, Зарплата]

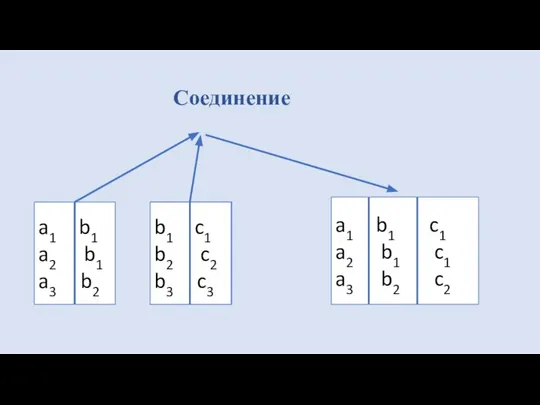
Специальные реляционные операторы
3
Соединением отношений А и В по условию С
называется отношение, образованное последовательностью операций декартова произведения и выборки:
(A TIMES B) WHERE C,
где С представляет собой логическое выражение, в которое могут входить атрибуты отношений А и В и (или) скалярные выражения.
Если в отношениях А и В имеются атрибуты с одинаковыми наименованиями, то перед выполнением соединения такие атрибуты необходимо переименовать.

Соединение
a1 b1
a2 b1
a3 b2
b1 c1
b2 c2
b3 c3
b1 c1
b2 c2
b3 c3
a1 b1 c1
a2 b1 c1
a3 b2 c2