Содержание
- 2. Логика это наука о законах и формах мышления. Основатель: Аристотель (384-322 до н.э.)
- 3. Алгебра логики Создана в 19 веке английским математиком Дж. Булем. Применяется для решения логических задач и
- 4. Логическое высказывание это повествовательное предложение, про которое можно однозначно сказать, истинно оно или ложно. A –
- 5. Составные высказывания Строятся из простых с помощью логических связок (операций) «и», «или», «не», «если … то»,
- 6. Высказывание или нет? Сейчас идет дождь. Жирафы летят на север. История – интересный предмет. У квадрата
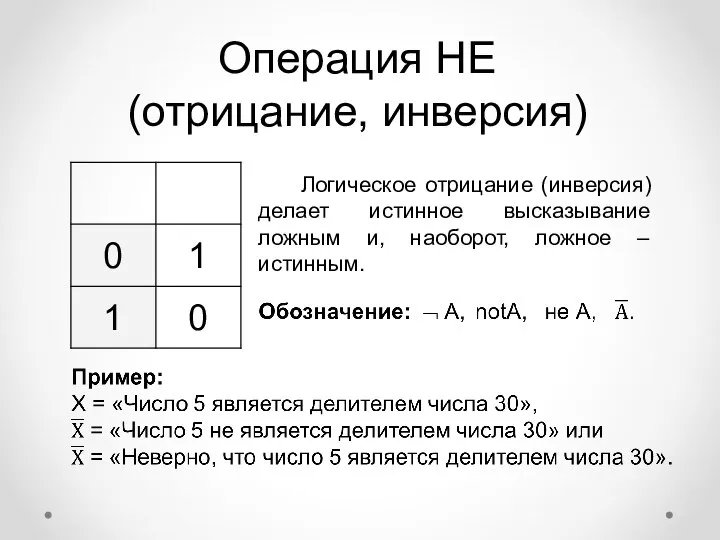
- 7. Операция НЕ (отрицание, инверсия) Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным.
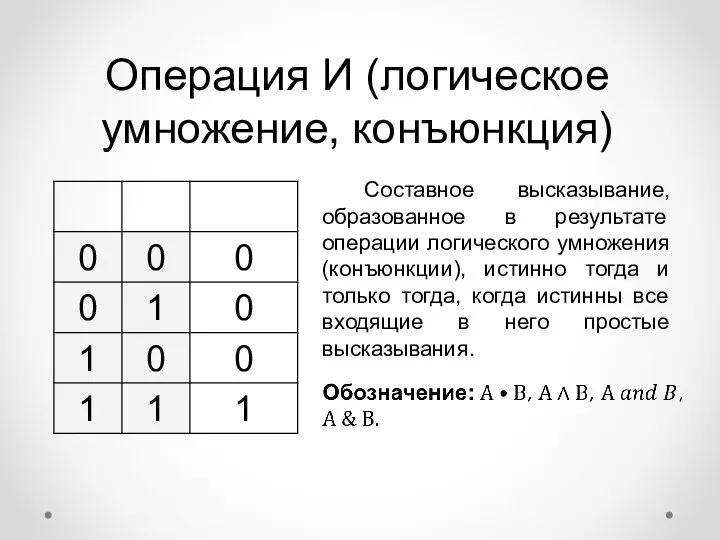
- 8. Операция И (логическое умножение, конъюнкция) Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда
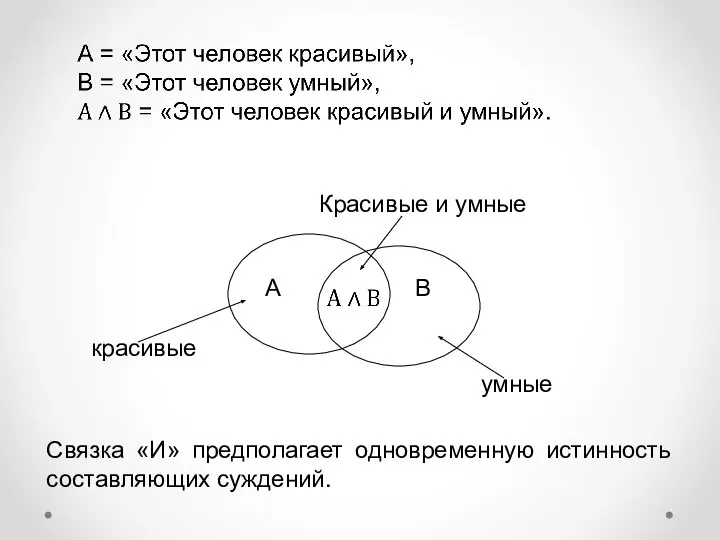
- 9. Связка «И» предполагает одновременную истинность составляющих суждений. А В Красивые и умные красивые умные
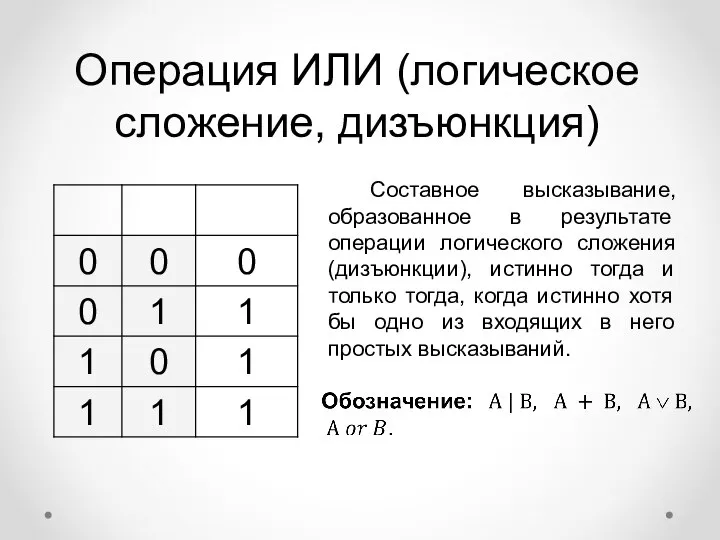
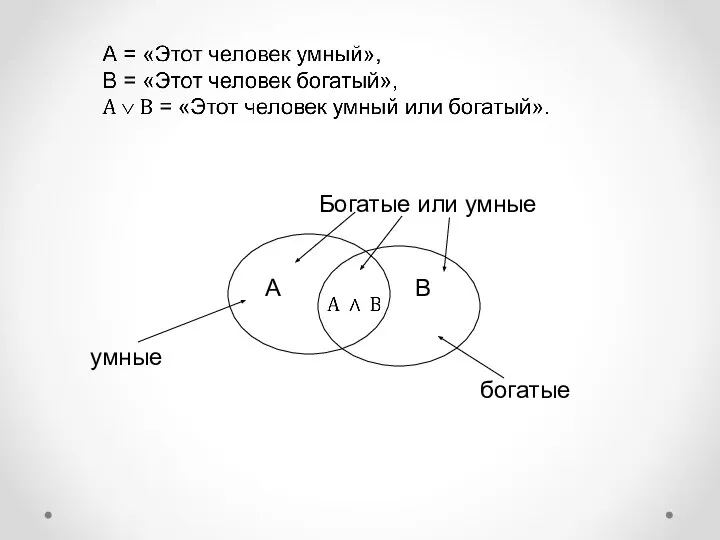
- 10. Операция ИЛИ (логическое сложение, дизъюнкция) Составное высказывание, образованное в результате операции логического сложения (дизъюнкции), истинно тогда
- 11. А В Богатые или умные умные богатые
- 12. Логическое следование (импликация) Это соединение двух высказываний с использованием оборотов речи «если ..., то», «из ...
- 13. Логическое следование (импликация) Составное высказывание, образованное с помощью операции логического следования (импликации), истинно тогда и только
- 14. Логическое равенство (эквивалентность) Это соединение двух высказываний А и В в одно с использованием оборота речи
- 15. Логическое равенство (эквивалентность) Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда,
- 16. Порядок выполнения операций инверсия; конъюнкция; дизъюнкция; импликация; эквивалентность.
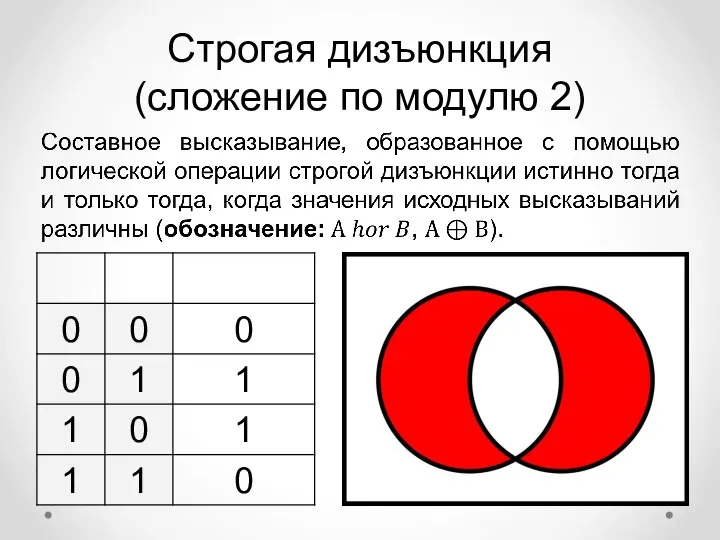
- 17. Строгая дизъюнкция (сложение по модулю 2)
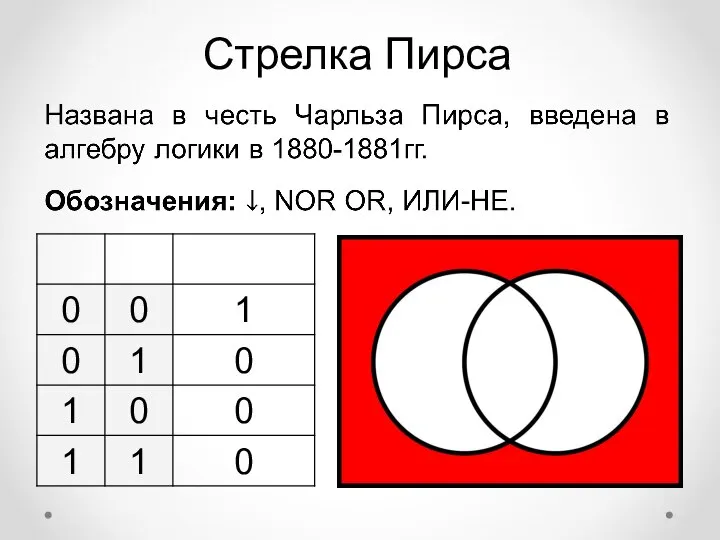
- 18. Стрелка Пирса
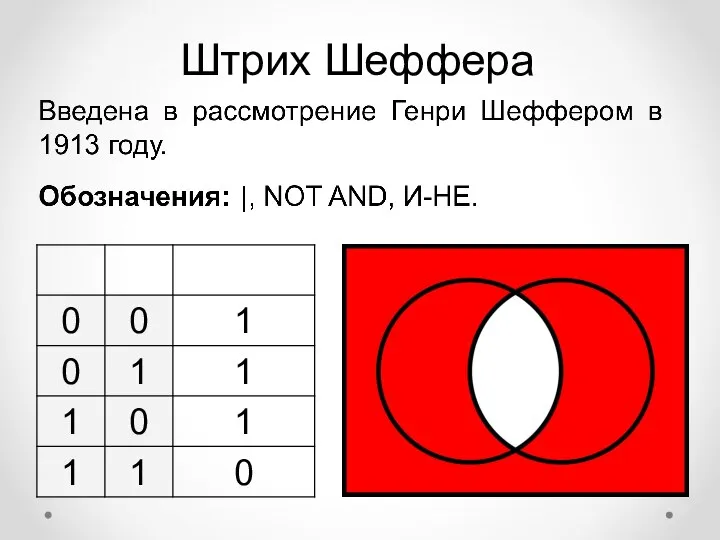
- 19. Штрих Шеффера
- 20. Алгоритм построения таблицы истинности
- 22. Скачать презентацию











 Web-страницы и Web-сайты
Web-страницы и Web-сайты Телевидение Persik. Инструкция по генерации кода
Телевидение Persik. Инструкция по генерации кода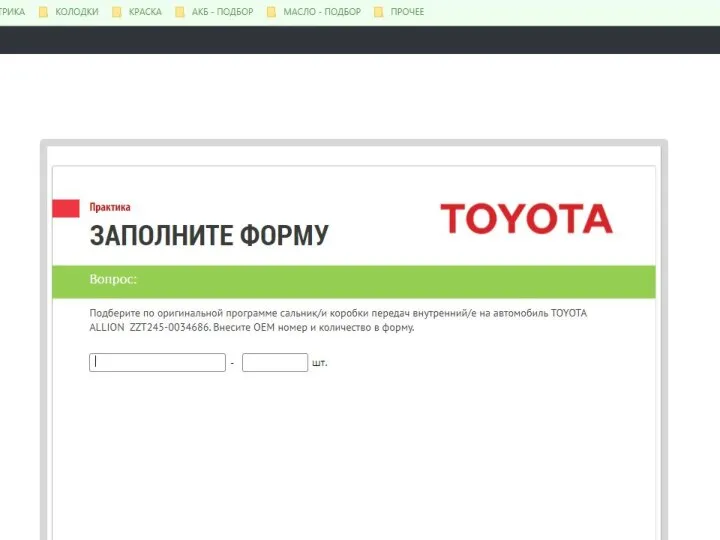 Сальник коробки
Сальник коробки Объектно-ориентированное программирование. Принципы ООП. Классы, объекты, поля и методы. Уровни доступа
Объектно-ориентированное программирование. Принципы ООП. Классы, объекты, поля и методы. Уровни доступа Конвертеры значений
Конвертеры значений BestProger. Изучайте программирование без лишней информации
BestProger. Изучайте программирование без лишней информации Вложенные циклы и двумерные массивы
Вложенные циклы и двумерные массивы Форматирование при подготовке документов на компьютере
Форматирование при подготовке документов на компьютере Объектная модель Excel
Объектная модель Excel Методология оптимизации параметров. Настройка параметров оптимизации
Методология оптимизации параметров. Настройка параметров оптимизации Вёрстка. Каркас сайта
Вёрстка. Каркас сайта Java_amm_lesson_3
Java_amm_lesson_3 Перемещение объектов. Урок 6
Перемещение объектов. Урок 6 Назначение программирования
Назначение программирования Программа 600 баллов, или ловля голавля
Программа 600 баллов, или ловля голавля Network computer technician
Network computer technician Латинский алфавит
Латинский алфавит ВКР: Проектирование распределённой мультисервисной сети по технологии GPON
ВКР: Проектирование распределённой мультисервисной сети по технологии GPON циклы Обмена отчеты ФНС
циклы Обмена отчеты ФНС Propaganda y publicidad
Propaganda y publicidad Компьютерная графика
Компьютерная графика ООП на Delphi
ООП на Delphi Вирусы и борьба с ними
Вирусы и борьба с ними Обгрунтування проектних рішень
Обгрунтування проектних рішень Информатика и Логика
Информатика и Логика Операционные системы: виды, назначение. Антивирусное ПО: виды назначение
Операционные системы: виды, назначение. Антивирусное ПО: виды назначение Язык программирования Pascal. Ветвление
Язык программирования Pascal. Ветвление Информационные технологии. Основные понятия
Информационные технологии. Основные понятия