Партнерская система ЗОРАН как система искусственного интелекта (часть вторая: интелектуальные функции)

09/12/2023
Партнерская Система ЗОРАН как система искусственного интелекта (часть вторая - интелектуальные функции) http://valspec.newmail.ru/
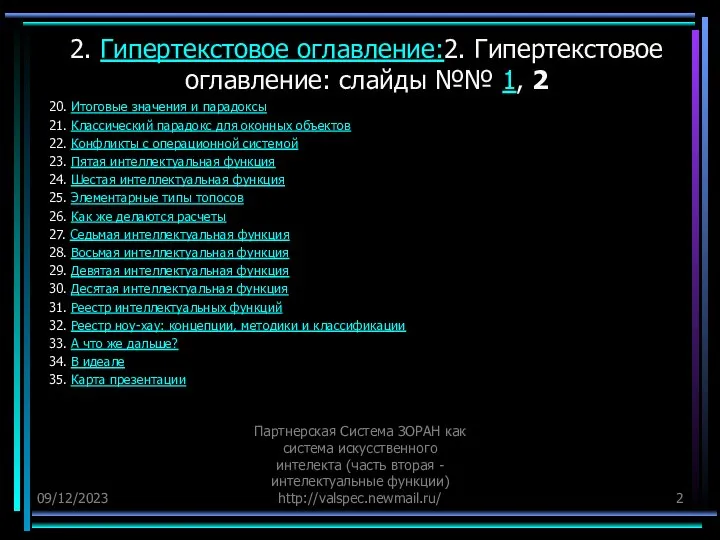
2. Гипертекстовое оглавление:2. Гипертекстовое оглавление: слайды №№ 1, 2
20. Итоговые значения и парадоксы
21. Классический парадокс для оконных объектов
22. Конфликты с операционной системой
23. Пятая интеллектуальная функция
24. Шестая интеллектуальная функция
25. Элементарные типы топосов
26. Как же делаются расчеты
27. Седьмая интеллектуальная функция
28. Восьмая интеллектуальная функция
29. Девятая интеллектуальная функция
30. Десятая интеллектуальная функция
31. Реестр интеллектуальных функций
32. Реестр ноу-хау: концепции, методики и классификации
33. А что же дальше?
34. В идеале
35. Карта презентации

3. Партнерская Система ЗОРАН
Служит яркой демонстрацией того, каким образом практически могут быть реализованы и использованы некоторые интеллектуальные функции, описанные в научной и фантастической литературе по искусственному интеллекту.

4. Экспертная система иного типа
С точки зрения теории, Партнерская Система ЗОРАН представляет собой экспертную систему, созданную на основе принципов так называемой W(доктор Уотсон)-технологии. То есть, эта система является своеобразным партнером человека-пользователя в решении большого количества экономических задач. С ее помощью пользователь всегда может получить обоснованный ответ на вопрос: ЧТО БУДЕТ, ЕСЛИ…

5. Классические экспертные системы; предел их возможностей
В отличие от Партнерской Системы ЗОРАН, обычные экспертные системы разрабатываются с использованием формально-логической М-технологии, со всеми ее преимуществами, ограничениями и недостатками. Базируются подобные системы на так называемой продукционной модели (совокупности большого количества правил ЕСЛИ … ТО …), обрабатываемой при помощи тех или иных концепций логического вывода: дедуктивного, индуктивного, абдуктивного, традуктивного и т.д. Любая же формально-логическая модель требует непротиворечивости внешних и внутренних данных, и не в состоянии из-за фундаментальных ограничений обрабатывать парадоксальные (хотя бы и контролируемые) ситуации.
В итоге, точно так же, как обычные компьютерные программы не могут преодолеть предел возможностей для точных расчетов, возможности классической формально-логической модели (и, соответственно, всех классических экспертных систем, созданных на ее основе) ограничиваются требованием непротиворечивости данных. Там же, где приходится сталкиваться с парадоксами или антиномиями, снова начинается масса проблем. И еще больше головной боли.

6. Преодоление предела возможностей классических экспертных систем
В отличие от традиционных экспертных систем, Партнерская Система ЗОРАН опирается не на формально-логическую, а на содержательно-эволюционную концепцию, что позволяет обрабатывать и учитывать в расчетах некоторые типы парадоксальных данных и ситуаций. К сожалению, фундаментальная теория парадоксов пока не создана, и вряд ли будет создана в обозримом будущем из-за полного равнодушия официальной науки к этой области знания. Поэтому, автору Партнерской Системы ЗОРАН пришлось эмпирическим путем создавать базу правил для корректного учета и обработки парадоксальных данных. В итоге получился своеобразный аналог ТРИЗа, отличающийся только тем, что теория решения изобретательских задач успешно помогает преодолевать технические и физические противоречия, а Партнерская Система ЗОРАН самостоятельно преодолевает информационные противоречия, возникающие особенно часто при использовании нечетких, зависимых и многовариантных данных.

7. Первая интеллектуальная функция
На данный момент не существует ни общепринятой классификации, ни исчерпывающего определения, ни фундаментальной теории парадоксов. С очень большой натяжкой парадоксом можно считать то или иное противоречие в том или ином интуитивном смысле, а также некоторые неоднозначности, странности, конфликты, коллизии, антиномии, взаимоисключающие друг друга данные в одном и том же численном или логическом значении и т.п. Данная трактовка совершенно не годится для формально-логической модели; но мы ведь опираемся на содержательно-эволюционный авторский подход. Так что никаких проблем. Поэтому будем с чистой совестью пользоваться преимуществами и выгодами выбранного метода, то есть от абсолютной объективности перейдем к относительной, опирающейся на волюнтаризм автора. В итоге, назовем первую реализованную интеллектуальную функцию Партнерской Системы ЗОРАН: субъективизм или авторское видение предметной области. Вообще, любая экспертная система представляет собой авторское видение предметной области, реализованное в виде экспертной базы непротиворечивых знаний и данных. Непротиворечивых потому, что эти знания и данные обрабатываются методами формальной логики. Ну а Партнерская Система ЗОРАН дополняет субъективизм очень важными особенностями.

8. Вторая интеллектуальная функция
И первая из этих особенностей – допустимость работы с парадоксальными в авторском понимании данными. Поэтому вторая интеллектуальная функция, реализованная в Партнерской Системе ЗОРАН – автоматическое преодоление противоречий-парадоксов с помощью специальной базы знаний и правил (парадоксализм). Разумеется, разрешаются отнюдь не все противоречия в объективном смысле, а только те, которые рассмотрены в авторской концепции искусственного интеллекта, классифицированы определенным образом как парадоксы, включены в соответствующую базу знаний, и встречаются при решении экономических задач. То есть в нашем случае парадоксализм контролируемый, а не бесконтрольный.

9. Классификация данных
А теперь самое время вспомнить все классы данных, описанные в первой части презентации и сведенные в единый реестр; в этот реестр вошли следующие данные:
Точные или четкие;
Нечеткие или неточные;
Неполные;
Неопределенные;
Зависимые;
Многовариантные;
Парадоксальные;
Распределенные;
Неявные.

10. Третья интеллектуальная функция
Еще одна особенность субъективизма – это возможность представления и обработки, наряду с обычными точными данными, в определенном смысле нестандартных типов данных: нечетких, неполных, неопределенных, зависимых, многовариантных, парадоксальных, распределенных и неявных. Таким образом, третья интеллектуальная функция, реализованная в Партнерской Системе ЗОРАН – автоматическое определение и автоматическая обработка точных, нечетких, неполных, неопределенных, зависимых, многовариантных, парадоксальных, распределенных и неявных данных (комплексный детерминизм). Приведенная классификация данных, естественно, субъективная, но зато очень удобная для проведения расчетов. Думается, что можно придумать и другие, ничуть не менее интересные классификации. Вопрос только в том, насколько это оправдано и эффективно. Кроме того, эта же классификация данных дает возможность, опираясь на нее, сформировать в первом приближении классификацию парадоксов – своего рода классификацию второго уровня. Дело здесь в том, что некоторые из приведенных типов данных могут становиться парадоксальными в тех или иных ситуациях. Ну а уж на базе классификаций можно легко сформулировать и реализовать корректные операции по обработке данных.

11. Итак, какие же парадоксы рассматриваются?
Парадоксы, связанные с обработкой точных данных;
Парадоксы, связанные с обработкой нечетких данных;
Парадоксы, связанные с обработкой зависимых данных;
Парадоксы, связанные с обработкой многовариантных данных;
Парадоксы, связанные с трактовкой окончательного результата итоговых расчетных данных;
Парадоксы, связанные с представлением и поведением окон диалоговых панелей и окон документов;
Парадоксы, связанные с потерей устойчивости в работе Партнерской Системы ЗОРАН из-за конфликтов с операционной системой.

12. Точные данные и парадоксы
Приведенные ниже примеры парадоксов для точных данных иллюстрируют ситуации и события, характеризующиеся большой неустойчивостью, требующие пристального внимания. Здесь: прогноз суммы – какую сумму предполагалось получить или потратить на первом этапе; после корректировки – откорректированная сумма на промежуточном этапе; результат, получили – окончательные данные.
Прогноз суммы 300, результат 0;
Прогноз суммы 300, результат –100;
Прогноз суммы –500, результат 0;
Прогноз суммы –500, получили 400;
Прогноз суммы 0, получили 300;
Прогноз суммы 0, результат –500;
Прогноз суммы 300, после корректировки –100, результат 0;
Прогноз суммы 300, после корректировки 0, результат –100;
Прогноз суммы –500, после корректировки 400, результат 0;
Прогноз суммы –500, после корректировки 0, получили 400;
Прогноз суммы 0, после корректировки 300, результат –200;
Прогноз суммы 0, после корректировки –500, результат 400.

13. Нечеткие данные и парадоксы (первый вариант)
Сразу следует отметить, что, всегда являясь неоднозначными, идеально отображая при этом недетерминированное будущее, нечеткие данные далеко не всегда парадоксальны. В отличие от них, точные данные всегда однозначны и отображают детерминированное будущее.
Итак, посмотрим на конкретных примерах, когда нечеткие данные парадоксальны, а когда нет.
140<>200 - данные неоднозначны, но не парадоксальны, так как в любом случае численное значение положительное;
-20<>-15 - данные неоднозначны, но не парадоксальны, так как в любом случае численное значение отрицательное;
0<>80 - данные неоднозначны и парадоксальны, так как численное значение либо равное нулю либо положительное;
-50<>0 – данные неоднозначны и парадоксальны, так как численное значение либо равное нулю, либо отрицательное;
-20<>40 – данные неоднозначны и парадоксальны, так как численное значение либо отрицательное либо равное нулю либо положительное.

14. Нечеткие данные и парадоксы (второй вариант)
Приведенные ниже примеры парадоксов для нечетких данных иллюстрируют ситуации и события, характеризующиеся большой неустойчивостью, требующие пристального внимания. Здесь: прогноз суммы – какую сумму предполагалось получить или потратить на первом этапе; после корректировки – откорректированная сумма на промежуточном этапе; результат, получили – окончательные данные.
Прогноз суммы 300<>400, результат 0;
Прогноз суммы 300<>400, результат –100;
Прогноз суммы –500<>–400, результат 0;
Прогноз суммы –500<>–400, получили 400;
Прогноз суммы –100<>0, получили 300;
Прогноз суммы 0<>200, результат –500;
Прогноз суммы 300<>400, после корректировки –100<>–50, результат 0;
Прогноз суммы 300<>400, после корректировки 0<>100, результат –100;
Прогноз суммы –500<>–400, после корректировки 400<>500, результат 0;
Прогноз суммы –500<>–400, после корректировки –200<>0, получили 400;
Прогноз суммы 0<>50, после корректировки 300<>500, результат –200;
Прогноз суммы –200<>0, после корректировки –500<>–400, результат 400.

15. Зависимые данные и парадоксы (первый вариант)
Пример логически непротиворечивой цепочки из 5 событий:
кредит в банке => покупка товара => продажа товара => возвращение кредита => прибыль
Эту цепочку можно упростить, если привести ее к парадоксальному виду:
продажа товара => покупка товара => прибыль
В самом деле, если есть постоянный клиент, который готов внести предоплату хотя бы за 2-3 недели вперед, то это гораздо выгоднее и удобнее первого варианта.
Так что парадоксальные преобразования зависимых данных часто позволяют получать простые и эффективные решения.

16. Зависимые данные и парадоксы (второй вариант)
Предположим, что из 50 событий составлен бизнес-план. Вероятность каждого события равна 0.99 (99 процентов). Если рассчитать бизнес-план без учета зависимых данных, то получим суммарную вероятность 0.99. Если же учесть, что 30 событий из этого бизнес-плана объединены в цепочку зависимых данных, то суммарная вероятность этой цепочки будет равна 0.74 (не очень-то и много!), а суммарная вероятность всего бизнес-плана окажется в интервале 0.74<>0.99.
Обычно, работая даже с точными данными, зависимости и вероятности не рассматривают вообще. И очень часто на этом теряют деньги.
В итоге, если рассмотреть оба решения, то вероятность окажется равной или строго 0.99 или нечетко 0.74<>0.99; таким образом, в первом случае мы получаем частное и потому неадекватное решение.
Введение концепции зависимых данных позволяет разрешать, в том числе, и именно такие противоречия-парадоксы.

17. Многовариантные данные и парадоксы (первый вариант)
Так как в многовариантных данных каждый исход может представлять собой как точное, так и нечеткое значение, в этом типе данных могут встречаться все типы парадоксов, рассмотренные для точных и нечетких данных.
Далее рассмотрим примеры парадоксов, характерные только для многовариантных данных:
В событии два исхода; при этом значение суммы первого равно 500, значение суммы второго равно 0.
В событии два исхода; при этом значение суммы первого равно -300<>-200, значение суммы второго равно 0.
В событии два исхода; при этом значение суммы первого равно
-100, значение суммы второго равно 300<>400.
В событии три исхода; при этом значение суммы первого равно 500, значение суммы второго равно 0, значение суммы третьего равно -300.

18. Многовариантные данные и парадоксы (второй вариант)
Следующий тип парадоксов, связанный с многовариантными данными, относится к расчету вероятностей. Непротиворечивая вероятностная модель выдвигает требование, чтобы суммарная вероятность всех исходов любого события не превышала единицы (100%). То есть, если событие состоит из двух исходов, то вероятности этих двух исходов могут быть равны, например, 0.4 и 0.6 (единица в сумме), но не 0.7 и 0.8 (1.5 в сумме). Партнерская Система ЗОРАН, наоборот, допускает возможность существования события, состоящего из десятков возможных исходов, вероятность каждого из которых близка или даже равна единице (мы ведь опираемся не на формально-логическую концепцию!). И здесь самое сложное не только определить подобные парадоксальные ситуации, но и корректно провести расчеты, чтобы полученный результата все-таки согласовывался со здравым смыслом. И только введение новой интеллектуальной функции позволило разрешать описанные противоречия.

Как Вы уже успели убедиться, Партнерская Система ЗОРАН позволяет составлять и рассчитывать бизнес-проекты состоящие из настоящей «каши» или мешанины фактов и значений, что стало возможным, благодаря введению интеллектуальных функций. Для многих типов данных одна из самых актуальных расчетных функций – способность к обобщению численных значений (обобщающая процедура). Это четвертая интеллектуальная функция, реализованная в Партнерской Системе ЗОРАН. Приведем пример. Пусть есть событие с тремя исходами. Значение суммы для каждого исхода равно соответственно: –200<>–1; 0; 1<>50. А значение вероятностей равно: 0.7; 0.8; 0.9. После реализации обобщающей процедуры итоговая сумма сумма займет интервал –200<>50. Как видим, любой интервал подобного рода – это неявное многовариантное событие с неопределенным количеством исходов. Ну а итоговая вероятность впишется в интервал 0.7<>0.9, а не составит совершенно бессмысленное значение 2.4. Так что без совокупности правил, входящих в состав обобщающей процедуры возможность проведения корректных расчетов выглядит весьма проблематичной.
19. Четвертая интеллектуальная функция

20. Итоговые значения и парадоксы
Парадоксы в итоговых расчетных значениях чаще всего встречаются тогда, когда бизнес-проекты анализируются на устойчивость. В частности, такой парадоксальный результат получился в примере для интернет-консалтинговой фирмы. В этом примере проводится анализ на устойчивость сопоставлением результатов расчетов первичных данных и данных с учетом того, что существует нелинейная тенденция к прогрессирующему снижению доходов. В итоге было получено: общая сумма для первоначальных данных 67845<>79341; общая сумма при уменьшении доходности 59596<>80392; неопределенность по сумме для первоначальных данных 14.48%; неопределенность по сумме при уменьшении доходности 25.86%; рентабельность для первоначальных данных 1.6<>1.75; рентабельность при уменьшении доходности 1.55<>1.8. То есть возникла ситуация, противоречащая здравому смыслу, когда при уменьшении доходности появилась теоретическая возможность на 5% увеличить рентабельность и более чем на 1000$ увеличить итоговую сумму; ну а проект оказался сверхустойчивым.

21. Классический парадокс для оконных объектов
Практически каждый оконный объект Партнерской Системы ЗОРАН (за исключением инструментальных панелей) может вести себя в определенном смысле парадоксальным образом. А именно: все диалоговые панели и документы в состоянии дублировать сами себя, причем копии-дубли ведут себя совершенно независимо от оригинала. Ну а объекты-документы, к тому же, могут быть разделены на части, причем каждая часть является полностью тождественным образом-копией соответствующего документа, но начинает при этом жить самостоятельной жизнью. Здесь реализован классический парадокс, когда часть ведет себя по отношению к целому, как целое по отношению к своей части. Данное свойство было названо асинхронной многоэкземплярностью.

22. Конфликты с операционной системой
Ну и, наконец, последний тип противоречий – это конфликты и коллизии, связанные со взаимодействием Партнерской Системы ЗОРАН с операционной системой типа Windows. Разработана и активно используется специальная база знаний и правил, позволяющая корректно выходить из возможный конфликтных ситуаций. Поэтому сообщение «Программа выполнила недопустимую операцию и будет закрыта» появляется крайне редко.

23. Пятая интеллектуальная функция
Следующая интеллектуальная функция – это способность к самоорганизации (процедура самоорганизации). Для решения различных экономических задач требуется строить разнообразные структуры в памяти, подчас весьма сложные, каждый раз оригинальные, предназначенные для решения только одной конкретной задачи. То есть внутренняя структура памяти Партнерской Системы ЗОРАН видоизменяется независимо от пользователя при расчетах экономических задач. А это очень удобно, потому что пользователь, таким образом, освобождается от необходимости получать ответ на вопрос: КАК ЭТО ДОЛЖНО БЫТЬ РЕАЛИЗОВАНО? Вместо это решается другой вопрос: ЧТО ДОЛЖНО БЫТЬ РЕАЛИЗОВАНО?

24. Шестая интеллектуальная функция
Еще более важная интегральная интеллектуальная функция – автоматическая генерация математических формул и получение итоговых результатов на основе этих формул (автоматизированная расчетная процедура). Данная функция интегральная, потому что опирается на уже рассмотренные интеллектуальные функции: парадоксализм, комплексный детерминизм, обобщающую процедуру, процедуру самоорганизации, а также на авторскую концепцию расширенных множеств - топосов. Топос – это расширенное множество, которое, в отличие от классического множества, характеризуется не только количеством элементов, но также определенной структурой, семантикой (смыслом), прагматикой (финансовой значимостью) и обобщенной математической формулой, которая при расчетах трансформируется (раскрывается) в зависимости от количества элементов топоса-множества.

25. Элементарные типы топосов
В настоящее время авторская концепция включает в себя более десятка типов (классов) топосов, однако, существующая версия Партнерской Системы ЗОРАН в состоянии обрабатывать только три из них:
Во-первых, это совокупность независимых друг от друга событий (тип документа «КАРТОЧКА»).
Во-вторых, это цепочка зависимых событий (тип документа «ФАЙЛ»); применяется для отображения зависимых данных.
В третьих, это единственное событие с набором исходов (тип документа «ТАБЛИЦА»); применяется для отображения многовариантных данных.
Как видите, типы топосов тесно связаны с типами нестандартных данных, являются их структурным, семантическим и прагматическим отображением. Ну, а каждому типу топоса в Партнерской Системе ЗОРАН соответствует определенный класс документа.

26. Как же делаются расчеты
Сначала для финансового проекта осуществляется поиск всех финансовых документов (топосов) с одновременным созданием в памяти соответствующих структур. В итоге автоматически генерируется расчетная формула, состоящая из наборов мини-формул:
Для совокупностей независимых событий;
Для цепочек зависимых событий;
Для событий с наборами исходов.
Затем производится финансовый расчет (с разрешением противоречий):
Для совокупностей независимых событий суммы складываются (вычитаются), а вероятности обобщаются;
Для цепочек зависимых событий суммы складываются (вычитаются), а вероятности перемножаются;
Для событий с наборами исходов суммы и вероятности обобщаются;
Одновременно, из данных промежуточных расчетов вычисляется итоговый результат (суммы складываются (вычитаются), а вероятности обобщаются);
И параллельно, на основе следующей интеллектуальной функции, производится распределение сумм по вероятностным интервалам.

27. Седьмая интеллектуальная функция
Крайне важна для окончательной трактовки результатов. Она названа пессимистическим видением мира (пессимистической процедурой) и основывается на втором начале термодинамики (в замкнутой системе хаос стремится к максимуму), а также на эмпирическом наблюдении: бутерброд всегда падает маслом вниз. То есть, в соответствии с пессимистической процедурой, всегда рассматривается худший или пессимистический результат (больше всего вероятности получить меньшую сумму, а не большую; больше всего вероятности потратить большую сумму, а не меньшую), по сравнению с наилучшим. Но, одновременно, этот худший результат является лучшим из худших результатов, которые обычно не рассматриваются, но при желании могут быть получены, благодаря еще одной интеллектуальной функции.

28. Восьмая интеллектуальная функция -
Введение и использование случайности (случайный фактор) для получения того или иного худшего результата, худшего на неопределенную величину, по сравнению с наилучшим из худших результатов. Опять все как в реальной жизни. Эта функция – побочный эффект от использования пессимистической процедуры; она особенно актуальна, когда огромный бизнес-проект приходится считать по частям из-за нехватки ресурсов операционной системы, или когда применяется ограниченная рабочая версия Партнерской Системы ЗОРАН. В итоге, если полученный Вами пессимистический результат выглядит прилично, значит, оптимистический результат будет от него отличаться на неопределенную величину в лучшую сторону.

29. Девятая интеллектуальная функция -
Поддержание гомеостаза (некоторого состояния равновесия внутренней среды Партнерской Системы ЗОРАН со внешней средой). Дело в том, что Партнерская Система ЗОРАН с самого начала разрабатывалась как псевдоживой, очень примитивный организм, с крайне ограниченным набором возможностей. Этот организм имеет центральную часть с функциями, аналогичными функциям центральной нервной системы, которая отвечает за корректные реакции на воздействия со стороны внешней среды – операционной системы. В зависимости от ситуации, центральная часть способна создавать разнообразные объекты, аналогичные псевдоподиям амебы, реагирующей на внешние раздражители. Ну а эти объекты, в свою очередь, обладают аналогом периферийной нервной системы. Таким образом, поддержание гомеостаза осуществляется на основе аналогов центральной и периферийной нервных систем, разработанных на базе методологии системного подхода.
Таких псевдоподий-объектов более сотни, причем каждый из них способен копировать самого себя либо непосредственно либо с помощью других объектов, то есть делиться на эквивалентные части, тождественные друг другу по внешнему виду и функциональным возможностям.

30. Десятая интеллектуальная функция -
Память о прошлой жизни. Здесь все очень просто. Если объект квазиживой, он должен обладать хоть какой-то памятью о прошлом. В последней версии Партнерской Системы ЗОРАН эта функция реализована следующим образом. Информация, поступающая в некоторые периферийные объекты избирательно распознается в режиме реального времени, сопоставляется со строкой на естественном языке, и записывается в центральную память с указанием времени, если такая функция включена в главном меню.
Всего таких периферийных объектов около сотни, каждый из них может быть продублирован от трех до пяти раз, то есть существовать в количестве от четырех до шести экземпляров, каждый из которых может находиться в разных состояниях: дееспособном, восстановленном, фиктивно уничтоженном, спрятанном и т.п. (в разрешенных сочетаниях); причем любой экземпляр объекта реализует полный набор соответствующих функций. В итоге, мы имеем многие десятки тысяч возможных ситуаций; при этом любая из этих ситуаций распознается почти мгновенно и запоминается в центральной памяти. Комментарии, как говорится, излишни.

31. Реестр интеллектуальных функций
Итак, в Партнерской Системе ЗОРАН реализованы следующие интеллектуальные функции:
Субъективизм или авторское видение предметной области;
Парадоксализм – автоматическое преодоление противоречий-парадоксов;
Комплексный детерминизм – обработка нестандартных данных (точных, нечетких, неполных, неопределенных, зависимых, многовариантных, парадоксальных, распределенных и неявных);
Обобщающая процедура – способность к обобщению численных значений;
Процедура самоорганизации – способность к самоорганизации;
Автоматизированная расчетная процедура – автоматическая генерация математических формул и получение итоговых результатов на основе этих формул;
Пессимистическая процедура – пессимистическое видение мира;
Случайный фактор – введение и использование случайности;
Поддержание гомеостаза - некоторого состояния равновесия внутренней среды Партнерской Системы ЗОРАН со внешней средой;
Память о прошлой жизни.

32. Реестр ноу-хау: концепции, методики и классификации
Ну и, наконец, необходимо еще раз напомнить о том, что, все описанные выше особенности, используемые в Партнерской Системе ЗОРАН, удалось реализовать исключительно благодаря практическому применению результатов независимых научных исследований, проведенных автором. Эти результаты были получены заранее, задолго до начала работы над созданием Партнерской Системы ЗОРАН. Итак, перечислим самые важные из них:
Авторская концепция искусственного интеллекта (любая система искусственного интеллекта должна разрабатываться как очень примитивный квазиживой организм с реализацией наиболее важных его структур и функций);
Теория систем и системный анализ;
Авторская классификация типов данных, включая новые типы, потому что наше будущее не является жестко детерминированным и не может быть адекватно описано посредством только точных данных;
Авторская классификация парадоксов, она абсолютна необходима, потому что наш реальный мир очень часто оказывается парадоксальным, а это нельзя игнорировать;
Авторский реестр интеллектуальных функций, без реализации хотя бы пары из них нельзя говорить о том, что та или иная программа является системой искусственного интеллекта;
Авторская концепция информационных обобщений;
Авторский аналог теории решения изобретательских задач (ТРИЗа), благодаря его использованию появилась возможность корректно обрабатывать противоречия-парадоксы;
Авторская концепция расширенных множеств – топосов (для автоматической генерации математических формул и получения результатов на основе этих формул);
Методы теории вероятностей;
Методы нечеткой математики;
Авторская методика создания W(доктор Уотсон) партнерских экспертных систем.

33. А что же дальше?
Ну а дальше – эволюционное развитие фундаментальной теории, авторской концепции искусственного интеллекта, самой Партнерской Системы ЗОРАН, услуг, оказываемых на ее основе, методических указаний по ее использованию, интернет сервиса, а также добавление примеров решения оригинальных экономических задач.
Все это возможно при дальнейшем развитии финансовой базы, привлечении серьезных спонсоров, инвесторов, партнеров, промоутеров и клиентов. Буду благодарен за Вашу поддержку.

34. В идеале
Я БУДУ РАД ВИДЕТЬ ВАС В ЧИСЛЕ МОИХ СПОНСОРОВ, ИНВЕСТОРОВ, ПРОМОУТЕРОВ, ПАРТНЕРОВ И КЛИЕНТОВ