большая длина периода. Длина периода зависит от значений M, k и b. Теорема, которая приводится ниже, позволяет определить, возможно ли достижение периода максимальной длины для конкретных значений M, k и b.
Теорема. Линейная конгруэнтная последовательность, определенная числами M, k, b и r0, имеет период длиной M тогда и только тогда, когда:
числа b и M взаимно простые;
k – 1 кратно p для каждого простого p, являющегося делителем M;
k – 1 кратно 4, если M кратно 4.
Примеры использования линейного конгруэнтного метода для генерации случайных чисел:
Пример 1:
M = 2N, k = 3 + 8· q (или k = 5 + 8 · q), b = 0, r0 — нечетно .
Было установлено, что ряд псевдослучайных чисел, генерируемых на основе данных из примера 1, будет повторяться через каждые M/4 чисел. Число q задается произвольно перед началом вычислений, однако при этом следует иметь в виду, что ряд производит впечатление случайного при больших k (а значит, и q). Результат можно несколько улучшить, если b нечетно и k = 1 + 4 · q — в этом случае ряд будет повторяться через каждые M чисел. После долгих поисков k исследователи остановились на значениях 69069 и 71365.
Пример 2:
M = 231 – 1, k = 1 220 703 125, b = 7, r0 = 7
Генератор случайных чисел, использующий данные из примера 2, будет выдавать случайные неповторяющиеся числа с периодом, равным 7 миллионам.
Мультипликативный метод генерации псевдослучайных чисел был предложен Д. Г. Лехмером (D. H. Lehmer) в 1949 году.
МОДЕЛИРОВАНИЕ ПРОЦЕССОВ И СИСТЕМ. Лекция 6














 Киберфизическая поисковая ЭКОсистема
Киберфизическая поисковая ЭКОсистема Приложения для мобильных устройств
Приложения для мобильных устройств Безотходный образ жизни. Передача
Безотходный образ жизни. Передача Контент. Типы контента
Контент. Типы контента Текстурный анализ изображений
Текстурный анализ изображений Построение шнека в Kompas-3DLT
Построение шнека в Kompas-3DLT Сайт Thunkable. Списки и сохранение данных
Сайт Thunkable. Списки и сохранение данных Принцип временного разделения каналов. Система передачи
Принцип временного разделения каналов. Система передачи Кибербезопасность
Кибербезопасность Конфигурирование безопасной передачи информации
Конфигурирование безопасной передачи информации Практика в студенческом медиацентре Радио ПГУ
Практика в студенческом медиацентре Радио ПГУ Турнир программистов. 7 класс
Турнир программистов. 7 класс Version 1.0. Условия в Python. Условные операторы, условные конструкции, True/False
Version 1.0. Условия в Python. Условные операторы, условные конструкции, True/False Zombie Hunt. Play
Zombie Hunt. Play Понятие алгоритма. Исполнитель
Понятие алгоритма. Исполнитель Передача информации
Передача информации Кибер безопасность
Кибер безопасность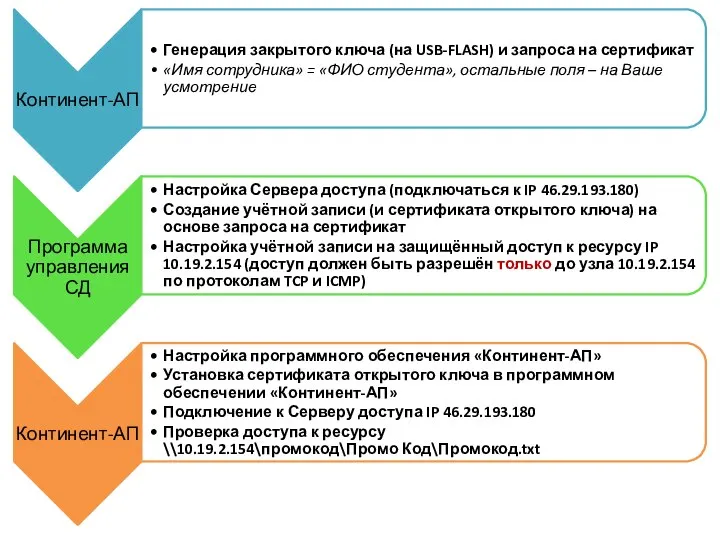 Континент-АП. Программа управления СД TCP и ICMP
Континент-АП. Программа управления СД TCP и ICMP Оператор div, mod в Pascal
Оператор div, mod в Pascal Токен ArtFinder
Токен ArtFinder Как найти свою первую работу программистом?
Как найти свою первую работу программистом? Функции. Обработка HTML-форм в РНР. Лекция 3
Функции. Обработка HTML-форм в РНР. Лекция 3 Группа Слава ВГУИТУ
Группа Слава ВГУИТУ Занятие 4. Понятие переменной. Арифметические действия. Команды ввода и вывода
Занятие 4. Понятие переменной. Арифметические действия. Команды ввода и вывода Разработка прототипа автоматизированной системы сбора, классификации и реферирования публикаций СМИ из новостных источников
Разработка прототипа автоматизированной системы сбора, классификации и реферирования публикаций СМИ из новостных источников Разработка ПО для автоматизации учета продажи обуви на предприятии “Престиж”
Разработка ПО для автоматизации учета продажи обуви на предприятии “Престиж” Разработка интернет магазина женской одежды при помощи CMS OpenCart
Разработка интернет магазина женской одежды при помощи CMS OpenCart Определи вид данного суждения
Определи вид данного суждения