Работа со строками. Класс String

Класс String является основным классом, предназначенным для хранения и обработки строк символов. Для создания экземпляров класса String может быть использован один из следующих конструкторов:
String()
String(String str)
String(StringBuffer strbuf)
String(char[] arr)
String(char[] arr, int first, int count)

Первый из них создаёт пустую строку, второй и третий копируют содержимое объектов классов String и StringBuffer в созданный объект. Последние два конструктора позволяют создать строку на основе символьного массива или его части.
Кроме того, любая объектная ссылка типа String может быть проинициализирована посредством присвоения ей строкового литерала, например:
String filename = "data.txt";

Особенностью класса String является то, что экземпляры этого класса не могут быть изменены после их создания. Однако это не создаёт ограничений для их использования, поскольку все методы, которые должны были бы изменять строку, просто создают новую модифицированную строку, оставляя исходную без изменений.

Поясним работу этого механизма на примере:
String s = "abcd";
s = s.toUpperCase();
Здесь метод toUpperCase() создаёт новую строку, содержащую последовательность символов "ABCD", и возвращает ссылку на эту строку, которая присваивается переменной s, старое значение переменной теряется. Исходная строка остаётся в неизменном виде и, поскольку на неё больше не осталось объектных ссылок, будет удалена сборщиком мусора.

Основные методы класса String

Преобразование к строке
Класс String является в некотором смысле исключительным классом в Java, поскольку любой тип данных может быть преобразован к нему.
Для примитивных типов такое преобразование даёт их естественное строковое представление, для объектов вызывается метод toString(), определённый в классе Object и, следовательно, присутствующий в любом классе Java.

Конкатенация строк
Для строк определена операция конкатенации, обозначаемая знаком +.
Это бинарная операция, один из аргументов которой должен иметь тип String. Она осуществляет автоматическое преобразование другого аргумента к типу String (если это необходимо) и слияние полученных строк. Это единственный случай, когда преобразование к строке осуществляется неявно.

Алгоритм поиска наидлиннейшей общей подпоследовательности строк

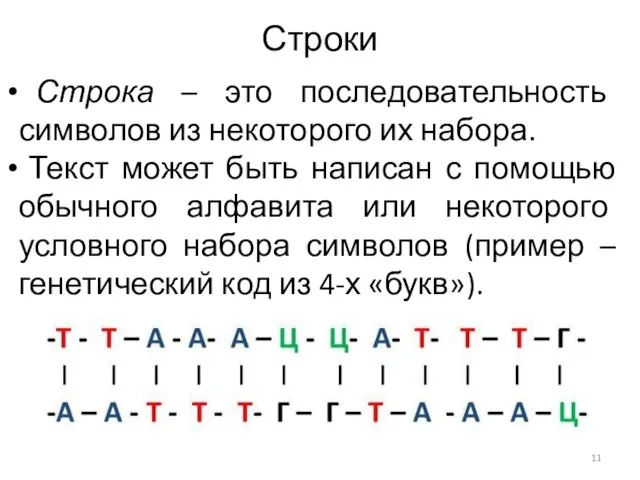
Строки
Строка – это последовательность символов из некоторого их набора.
Текст может быть написан с помощью обычного алфавита или некоторого условного набора символов (пример – генетический код из 4-х «букв»).

Последовательности и подпоследовательности
Последовательность представляет собой список элементов, в котором важен их порядок. Определенный элемент может появляться в последовательности несколько раз.
В нашем случае последовательности – это строки символов.
Подпоследовательностью Z строки X является строка X, возможно, с удаленными элементами.

1) GAC (без удаленных символов),
2) GA (удален С),
3) GC (удален А),
4) АС (удален G),
5) G (удалены А и С),
6) А (удалены G и С),
7) С (удалены G и А) и
8) пустая строка (удалены все символы).
Например, если X является строкой нуклеотидов GAC, то он имеет восемь подпоследовательностей:

Общая подпоследовательность
Если X и Y являются строками, то Z является общей подпоследовательностью X и Y, если она является подпоследовательностью обеих строк.
Например, если X — это строка CATCGA, а Y является строкой GTACCGTCA, то ССА является общей подпоследовательностью X и Y, состоящей из трех символов. Однако это не наидлиннейшая общая подпоследовательность, поскольку есть общая подпоследовательность СТСА из четырех символов.

Следует различать понятия подпоследовательности и подстроки: подстрока представляет собой подпоследовательность строки, в которой все символы выбираются из смежных позиций в строке. Для строки CATCGA подпоследовательность ATCG является подстрокой, в то время как подпоследовательность СТСА таковой не является.

Формулировка задачи
Задача: для двух заданных строк X и Y найти наидлиннейшую общую подпоследовательность (НОП) этих строк (обозначим ее Z).
Простой способ решения: перебор подпоследовательностей. Однако если длина X равна m, то она имеет 2m подпоследовательностей, что дает экспоненциальную зависимость времени поиска от длины X.

Динамическое программирование
Требуется: построить оптимальную подструктуру, т.е. оптимальное решение задачи должно состоять из оптимальных решений ее подзадач.
Оптимальная подструктура: наидлиннейшая общая подпоследовательность двух строк содержит в себе наидлиннейшие общие подпоследовательности префиксов этих двух строк.

Если X является строкой x1, x2, x3… xm, то i-м префиксом X является строка x1, x2, x3… xi, которую мы будем обозначать как Xi. Величина i должна быть в диапазоне от 0 до m, Х0 является пустой строкой.
Пример: если строка X — CATCGA, то Х4 — CATC.

Оптимальная подструктура
Наидлиннейшая общая подпоследовательность двух строк содержит в себе наидлиннейшие общие подпоследовательности префиксов этих двух строк.
Пусть две строки X = x1, x2, x3… xm и Y = y1, y2, y3… yn имеют некоторую наидлиннейшую общую подпоследовательность Z = z1, z2, z3… zk, где k может иметь значение от 0 до меньшего из значений m и n.
Посмотрим на последние символы строк X и Y: xm и yn.

а) Если xm и yn совпадают, последний символ zk строки Z должен быть таким же, как и этот символ. Остальная часть строки Z, т.е. Zk-1 = z1, z2, z3… zk-1, должна быть наидлиннейшей общей подпоследовательностью того, что осталось от X и Y, а именно — Хm-1 = x1, x2, x3… xm-1 и Yn-1 = y1, y2, y3… yn-1.

б) Если xm и yn различны, то zk может быть таким же, как хm или уn, но не оба. Кроме того, zk может не совпадать ни с последним символом X, ни с последним символом Y.
Если zk не совпадает с хm, игнорируем последний символ X: Z должна быть НОП Хm-1 и Y.
Аналогично, если zk не совпадает с уn, игнорируем последний символ Y: Z должна быть НОП X и Yn-1.

Подзадачи
Если xm и yn совпадают, то мы решаем только одну подзадачу — поиска НОП Хm-1 и Yn-1 — а затем добавим к ней этот последний символ, чтобы получить НОП X и Y.
Если xm и yn не совпадают, то нам надо решить две подзадачи — найти НОП Хm-1 и Y, а также X и Yn-1 — и использовать большую из них в качестве НОП X и Y. Если их длины одинаковы, можно использовать любую из них — конкретный выбор не имеет значения.

Вычисление длины НОП
Обозначим длину НОП префиксов Xi и Yj как l[i,j].
Длина НОП X и Y равна l[m,n].
Индексы i и j начинаются с 0, т.е. l[0,j] = l[i,0] = 0.
Когда i и j положительны, имеем два варианта:
а) если хi = yj, то l[i,j] = l[i-l,j-l] + 1;
б) если хi ≠ yj, то l[i,j] равно наибольшему из значений l[i,j-1] и l[i-1,j].
Для вычисления l[i,j], где i и j > 0, нам необходимо сначала вычислить записи l[i,j-1], l[i-1,j] и l[i-l,j-l].

Процедура Compute-LCS-Table(X, Y).
Вход: X и Y – две строки длиной m и n соответственно.
Выход: массив l[0..m, 0..w]. Значение l[m,n] представляет собой длину наидлиннейшей общей подпоследовательности X и Y.
Шаги процедуры:
1. Пусть l[0..m, 0..n] представляет собой новый массив.
2. Для i = 0 до m:
А. Установить l[i,0] = 0.
3. Для j = 0 до n:
А. Установить l[0,j] = 0.

4. Для i = 1 до m:
А. Для j = 1 до n:
i. Если хi совпадает с yj, то установить
l[i,j] = l[i-1, j-1] + 1.
ii. В противном случае (хi отличается от
yj) установить l[i,j] равным большему
из значений l[i, j-1] и l[i-1, j].
Если l[i, j-1] = l[i-1, j], конкретный
выбор не имеет значения.
5. Вернуть массив l.

Пример: последовательности нуклеотидов
Т.к. таблица содержит (m + 1)(n + 1) записей, время работы процедуры Compute-LCS-Table равно Θ(mn).

Определение самой НОП
Это рекурсивная процедура, которая собирает искомую подпоследовательность в обратном порядке – с конца к началу.
Когда она находит в X и Y одинаковые символы, она добавляет этот символ к концу строящейся наидлиннейшей общей подпоследовательности.

Процедура Assemble-LCS(X, Y, l, i, j).
Вход:
• X и Y – две строки,
• l – массив, заполненный процедурой Compute-LCS-Table,
• i и j – индексы как в строках Х и У, так и в массиве l.
Выход: наидлиннейшая общая подпоследовательность Xi и Yj.
Шаги процедуры:
1. Если l[i,j] = 0, вернуть пустую строку.

2. В противном случае (поскольку l[i,j] > 0 и i и j >0), если хi = yj, вернуть строку, образованную рекурсивным вызовом Assemble-LCS(X, Y, l, i-1, j-1) с добавлением к ней символа хi (или yj).
3. В противном случае (хi ≠ yj), если l[i, j-1] > l[i-1, j], вернуть строку, образованную рекурсивным вызовом Assemble-LCS(X, Y, l, i, j-1).
4. В противном случае (хi ≠ yj и l[i, j-1] ≤ l[i-1, j]) вернуть строку, образованную рекурсивным вызовом Assemble-LCS(X, Y, l, i-1, j).

Пример
Так как в каждом рекурсивном вызове происходит уменьшение на единицу либо значения i, либо значения j, либо обоих одновременно, время работы процедуры Assemble-LCS равно О(m+n).