Распознавание образов в программировании

4.1. Машина (метод) опорных векторов
(SVM, Support Vector Machine – Вапник В. и др. – 60-80 годы)
Линейно разделимый случай
Имеется множество прецедентов (Ξ,Y) , где Ξ = {x1 ,..., xN} – обучающая выборка, а Y = (y1 ,..., y N) – множество меток двух классов ϖ1 и ϖ2 .
Требуется по обучающей выборке построить линейную решающую функцию f(x), которая удовлетворяла бы условию f(xi) > 0 для всех xi∈ ϖ1 ,
f(x i) < 0 для всех xi ∈ ϖ2 .
Эту задачу можно переформулировать следующим образом.
Найти линейную решающую функцию f(x), которая удовлетворяла бы условию
yi f(xi) > 1 для всех xi ∈ Ξ. (4.1)
yi ((w,xi) + b) ≥ 1, i = 1,..., N , (4.2)
где w – вектор весовых коэффициентов, b – некоторое число.
Тогда разделяющей два класса гиперплоскостью будет
(w,x) + b = 0.

Все гиперплоскости вида (w,x) + b′ = 0, где b′ ∈ (b –1, b +1)
также будут разделяющими (рис. 4.1).
Рис. 4.1
Расстояние между граничными гиперплоскостями
(w,x) – 1+ b = 0 и (w,x) + b + 1 = 0 равно
– нормальные уравнения этих гиперплоскостей.
– расстояния от гиперплоскостей до начала координат.

Рис. 4.1
Для надёжного разделения классов необходимо чтобы расстояние между разделяющими гиперплоскостями было как можно большим.
Ставится задача нахождения минимума квадратичного функционала ½ (w,w)
в выпуклом многограннике, задаваемом системой неравенств (4.2)
½ (w,w) → min;
yi ((w,xi) + b) ≥ 1, i = 1,..., N , (4.2).
Решение этой оптимизационной задачи равносильно поиску седловой точки
лагранжиана

Свойства Метода опорных векторов:
1) это наиболее быстрый способ нахождения решающих функций;
2) метод сводится к решению задачи квадратичного программирования в выпуклой
области, которая всегда имеет единственное решение;
3) метод находит разделяющую полосу максимальной ширины, что позволяет в
дальнейшем осуществлять более уверенную классификацию;
4) метод чувствителен к шумам и стандартизации данных;
5) не существует общего подхода к автоматическому выбору ядра (и построению
спрямляющего подпространства в целом) в случае линейной неразделимости классов.
Большой класс нейронных сетей можно представить в виде SVM с определёнными ядрами.

4.2. Классификация с помощью функции расстояния
Этот способ предполагает определение функции, оценивающей меру
принадлежности предъявленного для классификации образа x классу ωi ,
т.е. некоторой функции d(x, ωi) , которая удовлетворяла бы условию x∈ωi ,
если d(x, ωi) ≤ d(x, ωj) для всех j ≠ i
Чтобы определить меру принадлежности образа x классу ωi нужно выбрать способ
определения меры близости между двумя образами, между образом и классом и,
наконец, между двумя классами. Так как каждый образ x характеризуется некоторым
вектором признаков x , то меру близости между образами x и y можно задать с
помощью меры близости d(x,y) между векторами-образами x и y их признаков.

В качестве такой меры близости чаще всего используют метрику, т.е. такую
неотрицательную функцию
d : Rn × Rn → R+ ,
которая удовлетворяет условиям аксиомы метрики.
Пространство Rn с введённой метрикой называют метрическим пространством.
Векторы признаков, между которыми измеряется расстояние, могут иметь разную
размерность, разные порядки величин, различные приоритеты.
Поэтому, прежде чем использовать метрики, желательно нормализовать и
стандартизировать значения признаков.
Способы определения расстояния между вектором-образом и классом
Определение расстояния до центра класса.
Этот способ применяется в том случае, когда класс «хорошо описывается» одним
эталонным образом – центром класса (качество такого описания может быть
измерено величиной дисперсии элементов класса), а цена ошибки неправильной
классификации не очень велика. Этот способ согласуется с так называемым
«принципом компактности» в распознавании образов, согласно которому
векторы-образы одного класса должны быть «компактно» расположены в
пространстве признаков.

2. Метод ближайшего соседа.
В этом способе расстояние определяется в соответствии со следующим
алгоритмом:
а) Определяется тот элемент xs обучающей выборки, который ближе всего к
предъявленному образу x,
б) Проверяется условие: если xs∈ωj , то считается что и x∈ωj .
3. определение расстояния до эталонного образа.
Этот способ применяется в том случае, когда класс плохо описывается одним
эталонным образом – центром класса. Признаком такой ситуации является
большое значение дисперсии элементов класса. Но можно предположить, что
элементы класса будут «хорошо группироваться» вокруг нескольких
эталонных образов.
Другими словами, каждый класс описывается не одним, а несколькими
эталонными образами. В этом случае расстояние между вектором-образом x и
эталонным классом ωi сводится к вычислению расстояния между этим вектором
и ближайшим к нему эталонным образом данного класса:

Предположим, что имеется множество прецедентов, т.е. обучающая выборка Ξ = {x1 ,..., xN} в пространстве признаков и множество меток Y = {y1 ,..., yN} принадлежности классам.
Рассмотрим случай двух классов ω1 и ω2 . Через X1 и X2 обозначим их области предпочтения, а через Ξ1 и Ξ2 - прецеденты первого и второго классов соответственно.
Требуется найти такую решающую(дискриминантную) функцию d(x), чтобы d(x) > 0 для всех x∈ Ξ1 и чтобы d(x) < 0 для всех x∈ Ξ2 . Если считать, что
то требуется найти такую функцию d(x), чтобы yid(xi) > 0 для всех xi ∈ Ξ .
4.3. Метод потенциальных функций

Метод потенциальных функций связан с определением так называемой потенциальной функции u(x,y) , т.е. некоторой положительной функциии, принимающей тем большие значения, чем «ближе» точки x и y друг к другу.
Если векторы признаков рассматриваются в метрическом пространстве, то в качестве потенциальной функции u(x,y) можно выбрать функцию вида u(x,y) = ũ(d(x,y)), где d(x,y) – некоторая метрика, а ũ(t) положительная монотонно убывающая функция. Например
Если потенциал u1(x) > u2(x), то x∈ X1 . Если же u2(x) > u1(x) , то x∈ X2 .
Таким образом, функция
будет решающей (дискриминантной) функцией.
Лепский, Броневич, 2009. презентация

Решающая функция может и не содержать всех слагаемых и будет иметь вид (1)
где xj∈ Ξ – множество векторов обучающей выборки, wj – неизвестные коэффициенты.
Функцию (1) можно записать с помощью скалярного произведения:
d(x) = (w,u(x)) , где w = (wj) , u(x) = (u (x, xj)).
В методе потенциальных функций дискриминантная функция d(x) находится по обучающей выборке Ξ = {x1 ,..., xN} путём коррекции k–й аппроксимирующей функции dk(x) с помощью следующей рекуррентной процедуры:
dk+1(x) = dk(x) + rk+1u(x,x k+1), d0(x) ≡ 0, (2)
где { rk } – некоторая последовательность, которая должна быть такой, чтобы гарантировать сходимость в некотором смысле dk(x) к d(x) при k → ∞ .

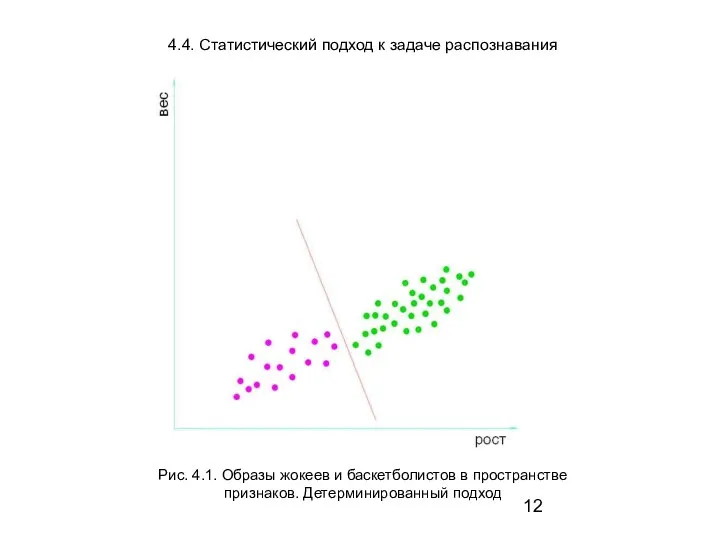
Рис. 4.1. Образы жокеев и баскетболистов в пространстве
признаков. Детерминированный подход
4.4. Статистический подход к задаче распознавания

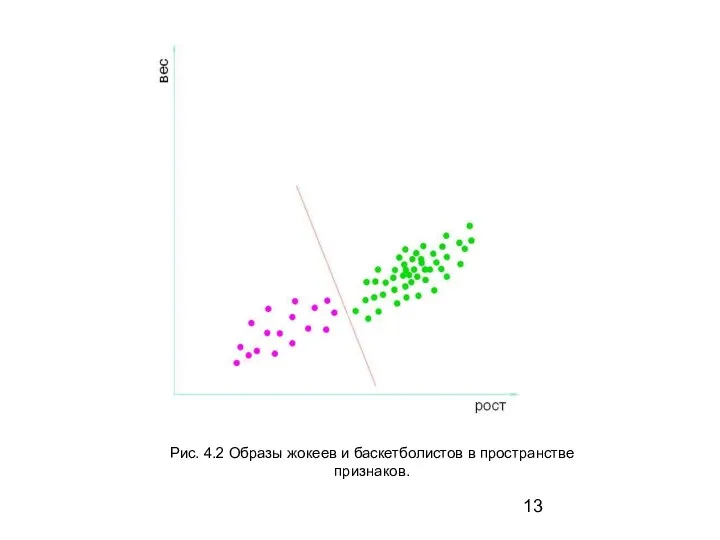
Рис. 4.2 Образы жокеев и баскетболистов в пространстве
признаков.

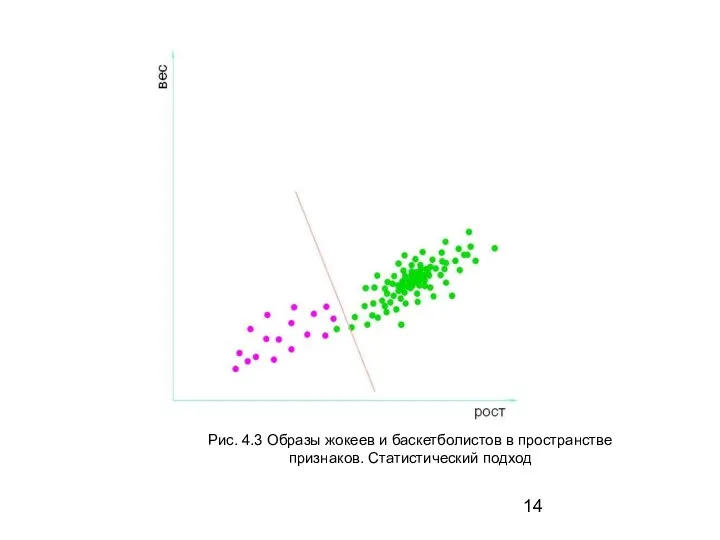
Рис. 4.3 Образы жокеев и баскетболистов в пространстве
признаков. Статистический подход

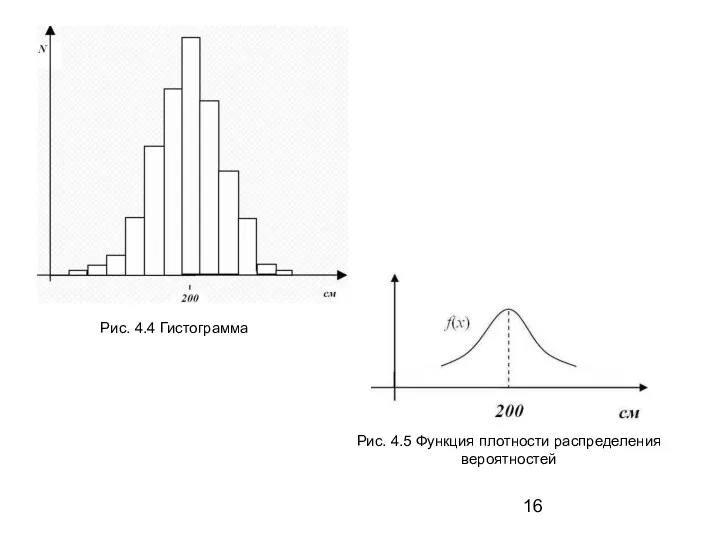
При большом количестве объектов относительную частоту появления
образа в классе можно оценить, построив гистограмму по объектам,
принадлежащим заданному классу.
При большом количестве образов в k-м
классе эта частота стремится к вероятности pk(x) появления образа x в данном
классе, и гистограмму можно рассматривать как дискретную аппроксимацию
функции плотности распределения fk(x).
В основе статистических методов классификации лежит предположение, что функция плотности вероятности f(x) для любого из выделяемых классов отлична от нуля на всем множестве значений признаков.
То есть любой вектор x может появиться в любом из классов, но с разной вероятностью.

Рис. 4.4 Гистограмма
Рис. 4.5 Функция плотности распределения
вероятностей

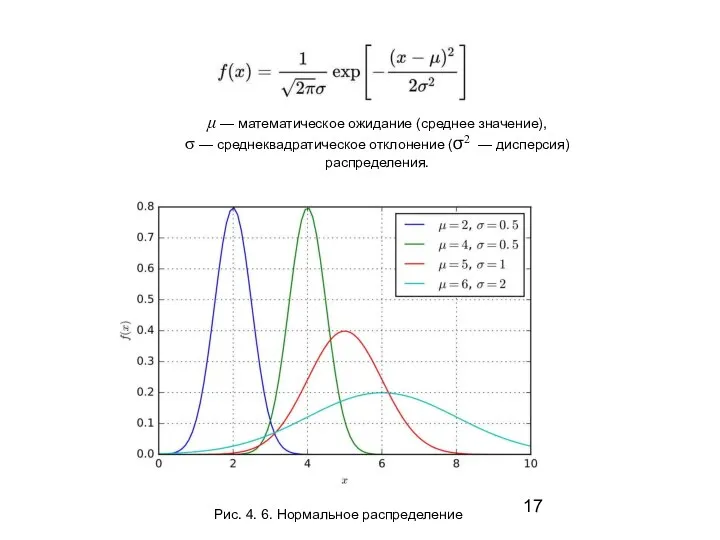
Рис. 4. 6. Нормальное распределение
μ — математическое ожидание (среднее значение),
σ — среднеквадратическое отклонение (σ2 — дисперсия) распределения.

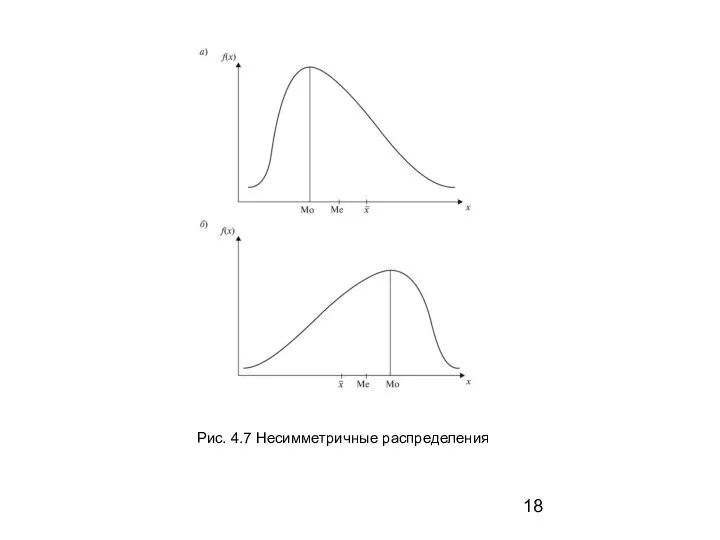
Рис. 4.7 Несимметричные распределения

В основе статистических методов классификации лежит предположение,
что функция плотности вероятности f(x) для любого из выделяемых классов
отлична от нуля на всем множестве значений признаков.
То есть любой вектор x может появиться в любом из классов, но с разной
вероятностью.
Поскольку мы неизбежно вынуждены строго определить границы
между классами в пространстве X, то всегда существует вероятность, что
какое-то количество точек из любого класса попадет в другие. Эта ошибка
называется ошибкой первого рода (α).
С другой стороны, в этот класс может попасть какое-то количество точек из
других классов. Такая ошибка называется ошибкой второго рода (β).
Полная вероятность ошибки выделения каждого класса,
таким образом, есть p(α) + p(β).
При большом количестве образов мы можем попробовать минимизировать
среднюю вероятность ошибки p(α) + p(β) при многократном принятии решения.

Критерий Байеса обеспечивает минимальную в среднем вероятность ошибки
распознавания при многократном принятии решения.
С этой целью вводится понятие «риска», то есть платы за каждую ошибку, и
определяется условие, соответствующее минимуму среднего риска.
Для пары классов Xi и Xj оно имеет следующий вид:
или в логарифмической форме
Поскольку мы ищем минимум среднего риска при многократном
принятии решения, в эти выражения, кроме функций плотности вероятности,
входят также априорные вероятности Pi и Pj ,
Можно сказать, что эти вероятности характеризуют частоту появления каждого
из классов на анализируемом множестве образов, которая пропорциональна доле
площади под этим классом.
(4.1)
(4.2)

Второе выражение (4.2) соответствует уже знакомому нам
виду разделяющей функции для пары классов: dij(x)=0 . То есть, если
Pifi(x) ≥ Pjfj(x) , то мы принимаем решение в пользу класса Xi , в противном
случае принимаем решение в пользу класса Xj .
Отношение (4.1) называется отношением правдоподобия, а функции,
стоящие в числителе и знаменателе, — функциями правдоподобия.
По-другому можно сказать,
что на каждом интервале мы принимаем решение в пользу того класса,
полная вероятность которого в рамках заданного множества образов
при конкретном значении x максимальна.
Такое правило принятия решения называют принцип максимума правдоподобия.
Ясно, что функция правдоподобия представляет собой решающую функцию.

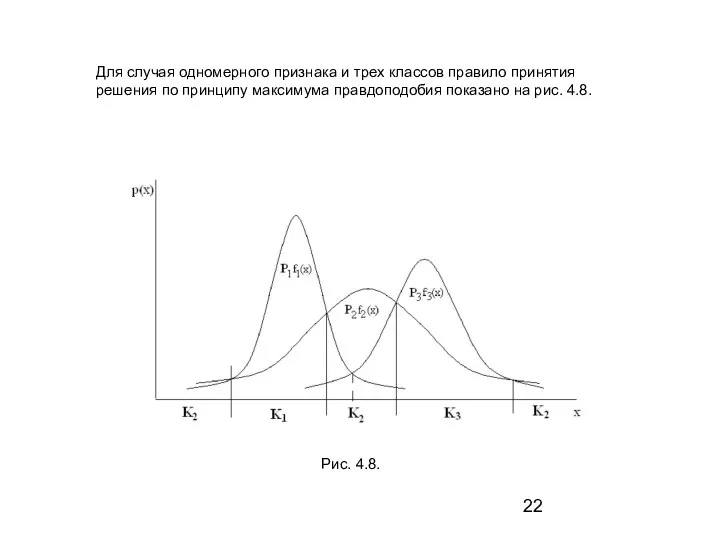
Для случая одномерного признака и трех классов правило принятия решения по принципу максимума правдоподобия показано на рис. 4.8.
Рис. 4.8.

Наиболее распространенные методы классификации без обучения:
ISODATA;
K-Средних.
Метод классификации без обучения ISODATA (Итерационная самоорганизующаяся
методика анализа данных - Iterative Self-Organizing Data Analysis Technique).
ISODATA это процесс, который основан на кластерном анализе.
Классификация без обучения(кластеризация)
1) Всё пространство признаков делятся на n равных множеств, для каждого из них
определяется среднее значение;
2) Первая итерация кластеризации: в пространстве для каждой точки
рассчитывается расстояние до средних значений, и каждую точку относят в
определенный кластер. В один кластер попадают те точки, между которыми меньше
расстояния в пространстве признаков;
3) Расчет новых средних значений для полученных классов;
4) Следующая итерация с новыми значениями средних, и уточнение границ
классов, при этом число классов может меняться.