Рекурсивный перебор с возвратом. Семинар для учителей информатики

ЗАДАЧА № 93. МИРНЫЕ ФЕРЗИ
Дано число N. Определите, сколькими способами можно расставить на доске N×N N ферзей, не бьющих друг друга.
Входные данные: задано единственное число (N ≤ 10)
Выходные данные: вывести количество способов, которыми можно расставить на доске N×N N ферзей, не бьющих друг друга.
Пример:
входные данные: 8
выходные данные: 92

КЛАССИЧЕСКИЙ СЛУЧАЙ: 8×8
Общее число возможных расположений 8 ферзей на 64-клеточной доске равно 4 426 165 368 = (64!/(8!(64-8)!)).
Очевидно, что на одной горизонтали или вертикали доски не может находиться больше одного ферзя, поэтому алгоритм решения изначально не должен включать в перебор позиции, где два ферзя стоят на одной горизонтали или вертикали. Даже такое простое правило способно существенно уменьшить число возможных расположений: 16 777 216 (то есть 88).

КЛАССИЧЕСКИЙ СЛУЧАЙ: 8×8
Генерируя перестановки, которые являются решениями задачи о восьми ладьях и затем проверяя атаки по диагоналям, можно сократить число возможных расположений всего до 40 320
(то есть 8!).

КЛАССИЧЕСКИЙ СЛУЧАЙ: 8×8
Один из типовых алгоритмов решения задачи — использование поиска с возвратом: первый ферзь ставится на первую горизонталь, затем каждый следующий пытаются поставить на следующую так, чтобы его не били ранее установленные ферзи. Если на очередном этапе постановки свободных полей не оказывается, происходит возврат на шаг назад — переставляется ранее установленный ферзь.

ПОДЗАДАЧА:
Даны координаты двух ферзей.
Определите, бьют ли они друг друга.
Входные данные: четыре числа.
Выходные данные: Yes или No.
Пример:
входные данные: 1 3 3 4
выходные данные: No

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ:
Ферзи бьют друг друга, если они находятся:
на одной горизонтали;
на одной вертикали;
на одной диагонали «юго-запад − северо-восток»;
на одной диагонали «юго-восток − северо-запад».
Проверка:
y1 = y2;
x1 = x2;
y1 – x1 = y2 – x2;
y1 + x1 = y2 + x2.

РЕАЛИЗАЦИЯ (PYTHON):
def check(x1, y1, x2, y2):
if y1 == y2 or x1 == x2 or
y1 - x1 == y2 - x2 or y1 + x1 == y2 + x2:
return True
return False

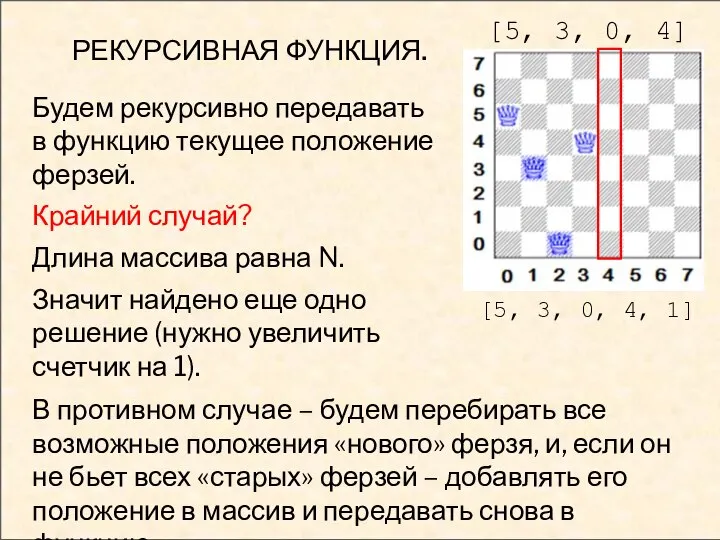
РЕКУРСИВНАЯ ФУНКЦИЯ.
Необходимо хранить текущую (промежуточную) «хорошую» расстановку части ферзей.
Как это сделать?
завести двумерный массив;
достаточно одномерного массива!
[5, 3, 0, 4]

РЕКУРСИВНАЯ ФУНКЦИЯ.
Будем рекурсивно передавать в функцию текущее положение ферзей.
Крайний случай?
Длина массива равна N.
Значит найдено еще одно решение (нужно увеличить счетчик на 1).
[5, 3, 0, 4]
В противном случае – будем перебирать все возможные положения «нового» ферзя, и, если он не бьет всех «старых» ферзей – добавлять его положение в массив и передавать снова в функцию.
[5, 3, 0, 4, 1]

РЕАЛИЗАЦИЯ РЕКУРСИВНОЙ ФУНКЦИИ:
def rec(prefix):
global count
if len(prefix) == n:
count += 1
return
for i in range(n):
f = True # флажок
for j in range(len(prefix)):
if check(len(prefix), i, j, prefix[j]):
f = False
break
if f:
rec(prefix + [i])
# Крайний случай

ОСНОВНАЯ ПРОГРАММА:
n = int(input())
count = 0
rec([])
print(count)

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ:
добавить визуализацию решений;
заработать миллион долларов:
Компьютерные программы перестают справляться с решением задачи, когда размер доски доходит до 1000 на 1000 клеток. Тот, кто сможет написать программу, способную решить задачу быстро, сможет адаптировать ее и для решения других важных проблем: «К ним относятся поиск самой большой группы друзей в Facebook, которые не знакомы друг с другом, или взлом кода, который защищает все наши операции в Интернете». Решение задачи о восьми ферзях эквивалентно решению одной из так называемых задач тысячелетия, а именно задачи о тождестве классов сложности Р и NP. За решение именно этой задачи Институт Клэя объявил награду в миллион долларов.

ЗАДАЧА № 94. МИРНЫЕ ФЕРЗИ
(БЕЗ ПОВОРОТОВ И ОТРАЖЕНИЙ)
Дано число N. Определите, сколькими способами можно расставить на доске N×N N ферзей, не бьющих друг друга. Расстановки ферзей, которые можно получить друг из друга поворотами и отражениями доски, нужно считать за одно.
Входные данные: задано единственное число (N ≤ 10)
Выходные данные: вывести количество способов, которыми можно расставить на доске N×N N ферзей, не бьющих друг друга.
Пример:
входные данные: 8
выходные данные: 12

12 УНИКАЛЬНЫХ (БЕЗ ПОВОРОТОВ И ОТРАЖЕНИЙ) РЕШЕНИЙ ЗАДАЧИ «МИРНЫЕ ФЕРЗИ» НА ДОСКЕ 8 × 8