Слайд 2Пример рекурсии
Если у вас жирное пятно на платье, не переживайте. Пятна от

масла убираются бензином. Пятно от бензина раствором щёлочи. Щелочь убирается эссенцией. След от эссенции потрите маслом. Hу, а как убрать пятна от масла, вы уже знаете!
Слайд 3Определение
Рекурсия (от латинского recursio - возвращение) - это такой способ организации вычислительного

процесса, при котором процедура или функция в ходе выполнения составляющих ее операторов обращается сама к себе.
Другими словами Рекурсия - подпрограмма, которая вызывает саму себя.
Слайд 4Пример вычисление факториала.
N! = 1*2*3* . . . *(N-2)*(N-1)*N
1! = 1
0! =

1
5! = 1*2*3*4*5 =120
Слайд 5Итеративная функция
Сначала покажем обычную не рекурсивную функцию для вычисления факториала, которая реализует
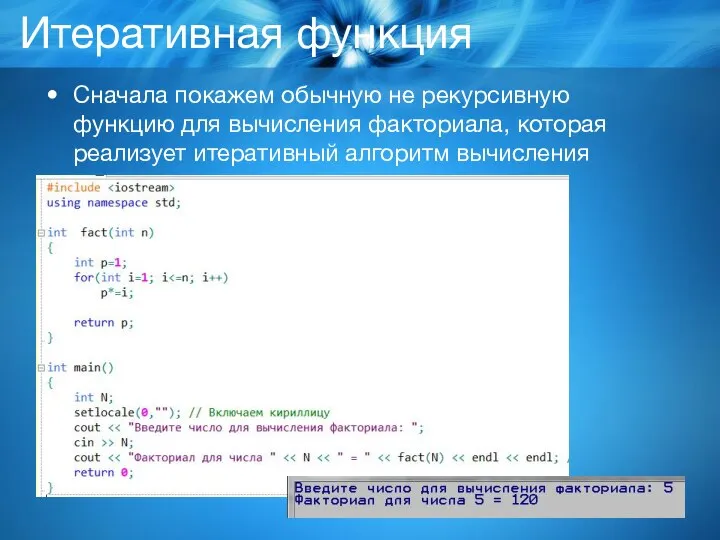
итеративный алгоритм вычисления
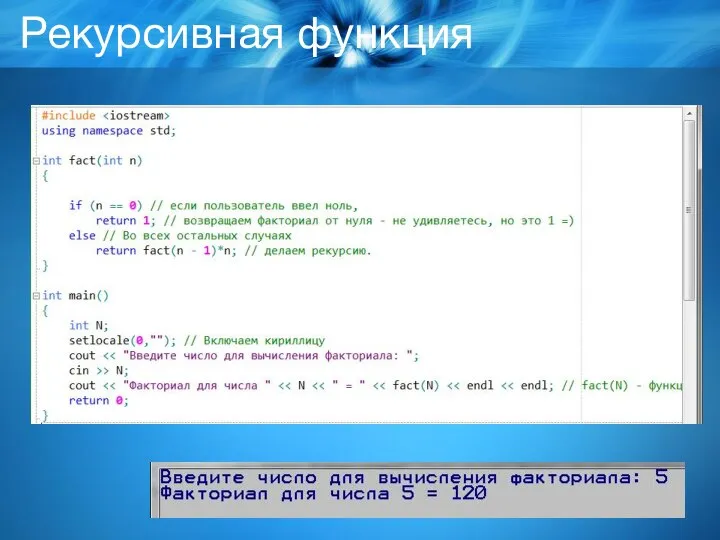
Слайд 6Вторая функция использует рекурсивные обращения, что делает ее гораздо компактнее, и основана

на очевидном соотношении:
N! = (N-1)!*N
Иными словами, чтобы получить значение факториала от числа N, достаточно умножить на N значение факториала от предыдущего числа:
5! = 4!*5
Слайд 8Пример вычислений
fact(5)=fact(4)*5
fact(4)=fact(3)*4
fact(3)=fact(2)*3
fact(2)=fact(1)*2
fact(1)=fact(0)*1
fact(0)=1
24*5=120
6*4=24
2*3=6
1*2=2
1*1=1
1

Слайд 9Таким образом можем сделать вывод, что рекурсию можем заменить на цикл (итерацию)

и наоборот.
Естественно, напрашивается вопрос – не получим ли мы бесконечный процесс рекурсивного вызова подпрограммы? Когда процесс «самовызова» остановится? Ответ – как только будет достигнуто условие, когда мы знаем ответ, не прибегая к рекурсии. Такое условие называется граничным.
Граничное условие – условие, при котором решение может быть получено нерекурсивно. Условие, при котором решение выражается с помощью более узкого варианта самого себя называется рекурсивным или общим условием.
Слайд 11Бесконечная рекурсия
Если граничное условие отсутствует, то получим бесконечную рекурсию – эквивалент бесконечного

цикла.
Бесконечная рекурсия – ситуация при которой подпрограмма бесконечно вызывает саму себя.
На самом деле, каждый раз, когда подпрограмма вызывает саму себя, используется дополнительная память для хранения новых копий переменных. В конце концов, свободной памяти не останется и программа даст сбой.
Слайд 12Косвенная рекурсия
Рекурсия может быть как прямой, когда программа вызывает саму себя, так

и непрямой (косвенной ) , когда программа вызывает другую программу, а та в свою очередь, вызывает первую программу.
При объявлении функций при непрямой рекурсии прототип второй функции описывается до описания первой.
Слайд 13Косвенная рекурсия
Образно косвенную рекурсию можно описать так. Перед зеркалом 1 стоит зеркало

2, в котором отражается само зеркало 1. В последнем видно зеркало 2 и т.д.
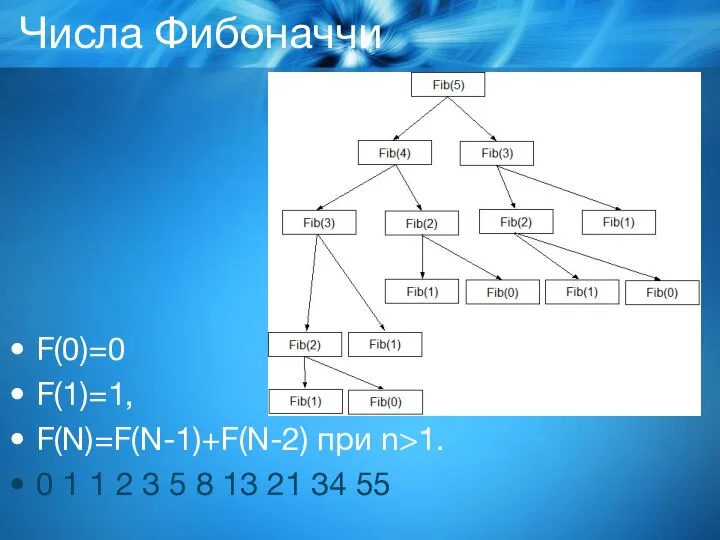
Слайд 15Числа Фибоначчи
F(0)=0
F(1)=1,
F(N)=F(N-1)+F(N-2) при n>1.
0 1 1 2 3 5 8 13
21 34 55
Слайд 17Числа Фибоначчи
Fib(5) = Fib(4)+Fib(3)
Fib(4) = Fib(3)+Fib(2)
Fib(3) = Fib(2)+Fib(1)
Fib(2) = Fib(1)+Fib(0)
Fib(1) = 1
Fib(0)

= 0
Слайд 18Степень числа
ab= a*a*…*a - b раз
или
ab=ab-1*a
int power(int a, int b)
{
if

(b == 0) return 1;
else return power(a, b - 1)*a;
}















 Формирование базы и экспертиза видеоконсультаций для подготовки к ГИА
Формирование базы и экспертиза видеоконсультаций для подготовки к ГИА Семантическое ядро, оптимизация разделов
Семантическое ядро, оптимизация разделов Алгоритмы с ветвлением
Алгоритмы с ветвлением Web-страницы. Язык HTML. Списки. Гиперссылки
Web-страницы. Язык HTML. Списки. Гиперссылки История развития HDD
История развития HDD Циклы по переменной. Программирование на языке Python
Циклы по переменной. Программирование на языке Python Нормально делай – нормально будет
Нормально делай – нормально будет HTML. WEB-сайты
HTML. WEB-сайты Запуск БС Huawei
Запуск БС Huawei Структуры и Файлы
Структуры и Файлы Операционные системы. Обзор Unix-операционных систем различных производителей
Операционные системы. Обзор Unix-операционных систем различных производителей Информационная безопасность как объект моделирования
Информационная безопасность как объект моделирования Выполнить задание и прислать результат в сетевом городе
Выполнить задание и прислать результат в сетевом городе Christmas & New Year at Canterville (slides carnival)
Christmas & New Year at Canterville (slides carnival) Операторы цикла
Операторы цикла Теория автоматов и формальных языков. Лекция 1
Теория автоматов и формальных языков. Лекция 1 Способы поиска в интернете
Способы поиска в интернете Круглый стол. Цифровая 3D-медицина. Тенденции развития научно-исследовательской работы студентов Арзамасского филиала ННГУ
Круглый стол. Цифровая 3D-медицина. Тенденции развития научно-исследовательской работы студентов Арзамасского филиала ННГУ Использование информационных и коммуникационных технологии в учебном процессе
Использование информационных и коммуникационных технологии в учебном процессе Формы в HTML
Формы в HTML Язык программирования Паскаль и его основные элементы
Язык программирования Паскаль и его основные элементы Комментарии к неправильной переадресации страниц
Комментарии к неправильной переадресации страниц TK
TK Программное управление исполнителями
Программное управление исполнителями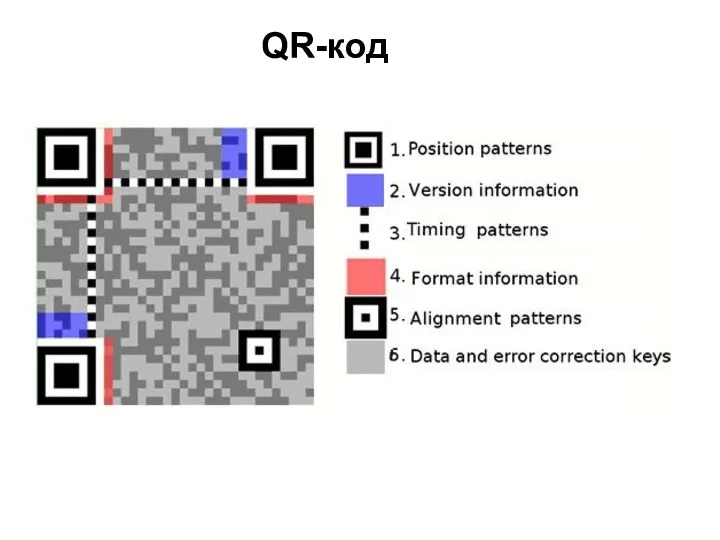 QR код
QR код Освоение технологии работы в графическом редакторе
Освоение технологии работы в графическом редакторе Информационные технологии в педагогическом процессе. Тема № 3
Информационные технологии в педагогическом процессе. Тема № 3 Технология проведения интернет-конференции Мосты науки
Технология проведения интернет-конференции Мосты науки