Лекция_Форм_вычисл_навыков

Методика работы над вычислительным приемом
Вычислительный прием складывается из группы операций. Все вычислительные приемы можно разделить на 6 групп:
1 группа: Т.О. - знание нумерации
а+1,
10+7, 17-7, 17-10,
40+3, 43-3, 43-40

Методика работы над вычислительным приемом
2 группа: Т.О. - смысл арифметических действий.
+ 2,3,4; табличные результаты и т. д.

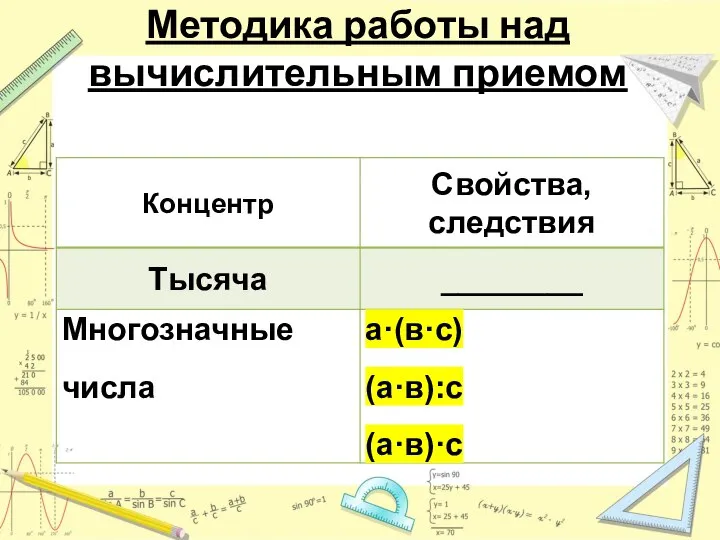
Методика работы над вычислительным приемом
3 группа: Т.О. - свойства арифметических действий

Методика работы над вычислительным приемом

Методика работы над вычислительным приемом

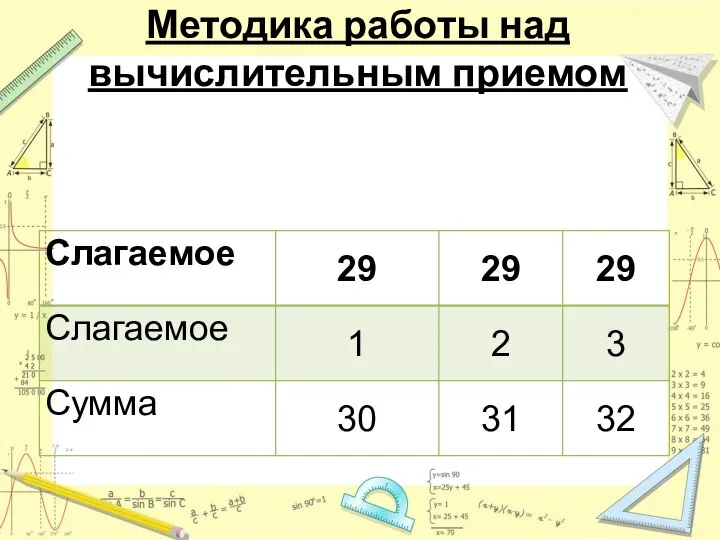
Методика работы над вычислительным приемом
4 группа: Т.О. - связь между компонентами и результатами действий
9 – 7 = 2 36 : 12 = 3
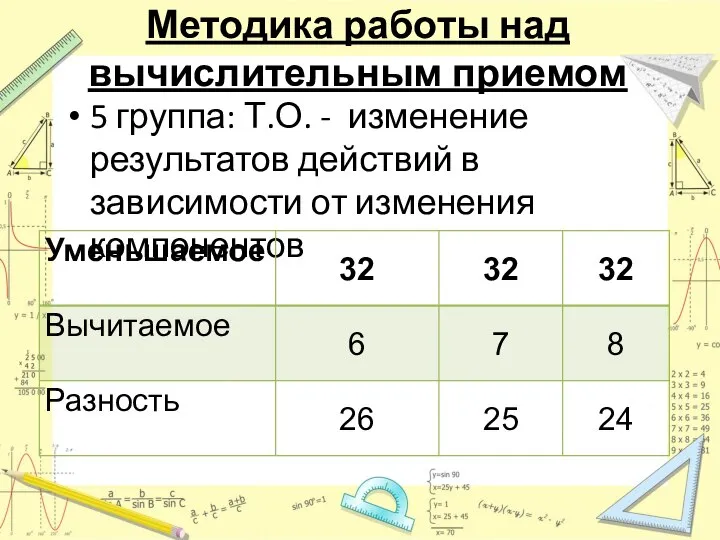
х + 5 = 8

Методика работы над вычислительным приемом
5 группа: Т.О. - изменение результатов действий в зависимости от изменения компонентов

Методика работы над вычислительным приемом

Методика работы над вычислительным приемом
6 группа: Т.О. – правила
а ⋅ 1, а ⋅ 0, 0 : а

Методика работы над вычислительным приемом
Работа над приемом дается по одному и тому же плану: подготовка, ознакомление, закрепление.
Подготовка.
Цель: подготовить к усвоению приема.
На этом этапе нужно:
отработать теоретические положения, на которых основан прием;
обеспечить овладение каждой операцией, составляющей прием

Методика работы над вычислительным приемом
Например:
12⋅ 6=(10+2)⋅ 6=10⋅ 6+2⋅ 6=60+12=72
разложить число на сумму разрядных слагаемых (10+2) ⋅ 6
отработать теоретическую основу (а+в)⋅ с
умножение разрядного числа на однозначное
табличное умножение
нахождение суммы двузначного разрядного числа и неразрядного.

Методика работы над вычислительным приемом
Можно считать, что дети подготовлены к усвоению приема, если:
есть знания десятичного состава числа
есть знания правила умножения суммы на число
овладели навыками:
чтения математических выражений
вычислительными навыками каждой операции

Методика работы над вычислительным приемом
Ознакомление
Цель: освоение сути приема.
12·6=(10+2)·6=10·6+2·6=60+12=72
Заменяю Получился Удобно Находим сумму
Ученики должны знать, какие операции надо выполнять, в каком порядке, почему. Этот этап идет в проработке вычислительного навыка, т.е. высокого овладения приемом (автоматизация)

Закрепление
Цель: формирование прочных вычислительных навыков (устных или письменных)
Реализуется через разнообразные упражнения (примеры, дидактические игры, тренажеры), задачи, уравнения

Пример-иллюстрация ко второй группе ВП (ТО – свойства арифметических действий)

Методика работы над вычислительным приемом
Для чего изучаются свойства арифметических действий?
Знание свойств углубляет знания об арифметических действиях и служит теоретической основой вычислительных приемов. В начальном курсе математики свойства даются в виде правил (следствий)

Методика работы над вычислительным приемом
На подготовительном этапе необходимо:
добиться хорошего усвоения терминологии, смысла действия, символов.
работать над математическими выражениями; накопить опыт в чтении и записи выражений (чтение разными способами).
научить заменять двузначное неразрядное число суммой разрядных слагаемых

Методика работы над вычислительным приемом
На этапе ознакомления раскрывается суть самого свойства. Необходимо показать свойство в практической ситуации. Использовать при этом дидактические материалы или сюжетную задачу

Методика работы над вычислительным приемом
Например:
Вычитание числа из суммы: (4+3)-2
В гараже 4 легковых машины и 3 грузовых. 2 машины уехали. Сколько машин осталось в гараже? Самостоятельно запишите и дайте объяснение 3 способам решения задачи.

Методика работы над вычислительным приемом
(4+3)-2=7-2=5
(4+3)-2=(4-2)+3=2+3=5
(4+3)-2=(3-2)+4=1+4=5

Методика работы над вычислительным приемом
Например: Умножение числа на произведение: а·(в·с)
2·(4·3)=2·12=24
2·(4·3)=(2·4)·3=8·3=24 2·(4·3)=(2·3)·4=6·4=24

Методика работы над вычислительным приемом
Выражения сравниваются: Если в левой части выражения одинаковы, значит и в правой одинаковы, а способы нахождения их значений различны.

Методика работы над вычислительным приемом
На этапе закрепления свойства закрепляются на специально подобранных упражнениях четырех видов:
прочитать выражение и найти его значение тремя различными способами
найти значение выражения удобным способом
преобразовать выражение «Закончи запись»
решить задачу различными способами
От школьников не следует требовать изучения свойства. Главное, чтобы они применяли его в вычислительных приемах.

Формирование вычислительных навыков
Качества навыка:
Правильность: правильно выбираются операции, составляющие прием; правильно выполняются; правильно находится результат арифметического действия
Осознанность: ученик осознает, на основе каких знаний выбраны операции (умение доказать)

Формирование вычислительных навыков
Качества навыка:
Рациональность: выбираются те операции, при помощи которых легче и быстрее получить результат
Автоматизация: операции выполняются быстро и в свернутом виде

Формирование вычислительных навыков
Качества навыка:
Прочность: сформированные навыки сохраняются на длительное время
Обобщенность: знания применяются к большому числу случаев

Формирование вычислительных навыков
В формировании вычислительного навыка выделяют 4 стадии:
стадия развернутого действия – ученики выполняют все операции составляющие прием, комментируют все операции, производят длинную запись
Не следует долго задерживаться на этой стадии

Формирование вычислительных навыков
стадия частичного свертывания – про себя выделяют операции и обосновывают выбор и порядок их выполнения, вслух проговаривают выполнение основных операций
стадия полного свертывания – все операции проговариваются про себя, записывается только пример и ответ, объяснение дается
стадия предельного свертывания – быстро выполняется прием без объяснения

Устные и письменные вычисления
Вычисления, проводимые без вспомогательных средств – таблиц и счетных приборов, подразделяются на устные и письменные.
Общее:
имеют общую задачу – найти искомое
выполняются путем приведения данного случая вычисления к ранее известным (к табличным)
способы тех и других обосновываются свойствами арифметических действий
Письменные вычисления тесно связаны с устными, так как в процессе письменных вычислений приходится использовать устные. Поначалу учащиеся в основном выполняют устные вычисления

Отличия устных вычислительных приемов от письменных
Устные
1) Выполняются в уме (мысленно)
2) Выполняются совсем без записи чисел или с записью данных и результата в строчку
Письменные
1) Выполняются письменно (всегда)
2) В процессе выполнения записываются не только данные и результат, но и промежуточные результаты.
Записываются в столбик

Отличия устных вычислительных приемов от письменных
Устные
3) Сложение и вычитание начинаются с высшего разряда
4) Запись относительно произвольная
Письменные
3) Результат приема находим, начиная вычисления с низшего разряда (за исключением письменного деления)
4) Запись жестко определенная (разряд под разрядом)

Особенности устных вычислений
Успешность обучения письменным вычислениям зависит от навыков устных вычислений
Устные вычисления способствуют развитию математического мышления детей
Устные вычисления содействуют развитию внимания и памяти

К устным вычислениям относят все приемы для случаев вычислений в пределах 100, а также сводящиеся к ним приемы вычислений для случаев за пределами 100 (например: 900-300)
К письменным вычислениям относятся приемы, для всех других случаев вычислений над числами, большими 100

За 4 года обучения в начальных классах дети должны не только сознательно усвоить приемы устного вычисления, но и приобрести прочные вычислительные навыки, которые помогают:
Усвоить многие вопросы теории арифметических действий (свойства действий, связь между результатами и компонентами действий, изменение результатов действий в зависимости от изменений одного из компонентов)
Лучше усвоить приемы письменных вычислений, так как являются элементами последних
Успешно решать жизненные ситуации (имеют практическое применение в жизни)
Способствуют развитию математического мышления, внимания, памяти, сообразительности, математической зоркости и наблюдательности

Виды упражнений для устных вычислений
нахождение значений математических выражений
сравнение математических выражений
решение уравнений
решение задач