Содержание
- 2. СОДЕРЖАНИЕ Определение Непозиционные системы счисления Позиционные системы счисления Однородные системы счисления Смешанные системы счисления История систем
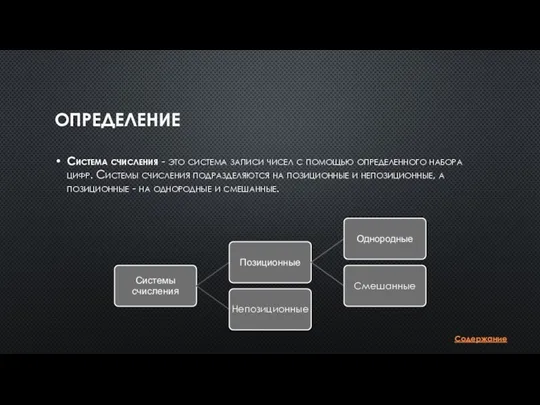
- 3. ОПРЕДЕЛЕНИЕ Система счисления - это система записи чисел с помощью определенного набора цифр. Системы счисления подразделяются
- 4. НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ В такой системе счисления каждая цифра имеет величину, не зависящую от позиции(разряда). Например,
- 5. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ В такой системе счисления значение каждой цифры зависит от её позиции(разряда). Так, привычная
- 6. ОДНОРОДНЫЕ СИСТЕМЫ СЧИСЛЕНИЯ В такой системе счисления для всех позиций(разрядов) набор допустимых чисел одинаков. Например, в
- 7. СМЕШАННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ В такой системе счисления для разных позиций(разрядов) набор допустимых чисел может отличаться. Это
- 8. ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ Как только люди научились считать — возникла потребность записи чисел. В начале все
- 9. ДРЕВНЕЕГИПЕТСКАЯ ДЕСЯТИЧНАЯ СИСТЕМА В Древнем Египте использовались специальные символы для обозначения чисел 1, 10, 102, 103,
- 10. ВАВИЛОНСКАЯ ШЕСТИДЕСЯТЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ В отличии от египетской, в вавилонской системе использовалось всего 2 символа: “прямой”
- 11. Запись числа была неоднозначной, поскольку не существовало цифры обозначающей ноль. Представление числа 92 могло обозначать не
- 12. РИМСКАЯ СИСТЕМА СЧИСЛЕНИЯ Римская система не сильно отличается от египетской. В ней для обозначения чисел 1,
- 13. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Первые предпосылки к появлению позиционной системы возникли в древнем Вавилоне. В Индии система
- 14. ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ Эта система, в основном, используется в вычислительной технике. Почему не стали использовать привычную
- 15. ВОСЬМЕРИЧНАЯ И ШЕСТНАДЦАТЕРИЧНАЯ СИСТЕМЫ СЧИСЛЕНИЯ 8-я система счисления, как и двоичная, часто применяется в цифровой технике.
- 16. Перевод из одной системы счисления в другую Преобразование в десятичную систему счисления Иногда требуется преобразовать число
- 17. Преобразование из десятичной системы счисления в другие Целая часть: Последовательно делим целую часть десятичного числа на
- 18. Преобразование из двоичной в восьмеричную и шестнадцатеричную системы Для перевода в восьмеричную — разбиваем двоичное число
- 19. Преобразование из восьмеричной и шестнадцатеричной систем в двоичную Перевод из восьмеричной в двоичную — преобразуем каждый
- 21. Скачать презентацию

















 Витраж. Алгоритм
Витраж. Алгоритм Клуб интеллектуальных игр Игры разума
Клуб интеллектуальных игр Игры разума Возможности настольных издательских систем. Организация и основные способы преобразования (верстки) текста
Возможности настольных издательских систем. Организация и основные способы преобразования (верстки) текста Data chief – С20
Data chief – С20 Тема 7.1. Линейный список
Тема 7.1. Линейный список Элементы алгебры логики. Математические основы информатики
Элементы алгебры логики. Математические основы информатики Моушен дизайн
Моушен дизайн Модели и моделирование. Информационное моделирование
Модели и моделирование. Информационное моделирование К Телеком. Модернизация домашней сети г. Богданович
К Телеком. Модернизация домашней сети г. Богданович Банки и базы данных
Банки и базы данных Меню программы PowerPoint
Меню программы PowerPoint Глобальная программа экономии бюджета Карта PRIZM c кэшбэком 20-50%
Глобальная программа экономии бюджета Карта PRIZM c кэшбэком 20-50% Библиотека села Ныр
Библиотека села Ныр Схема взаимодействия сторон в рамках проекта Партнерский
Схема взаимодействия сторон в рамках проекта Партнерский Написание тест-кейсов
Написание тест-кейсов Рунет: жизнь на яркой стороне
Рунет: жизнь на яркой стороне Blogosphere as an element of the modern media field as an element of the modern media field
Blogosphere as an element of the modern media field as an element of the modern media field Работа с ПК. Тема 1 занятие 2
Работа с ПК. Тема 1 занятие 2 Основные принципы алгоритмизации и программирования
Основные принципы алгоритмизации и программирования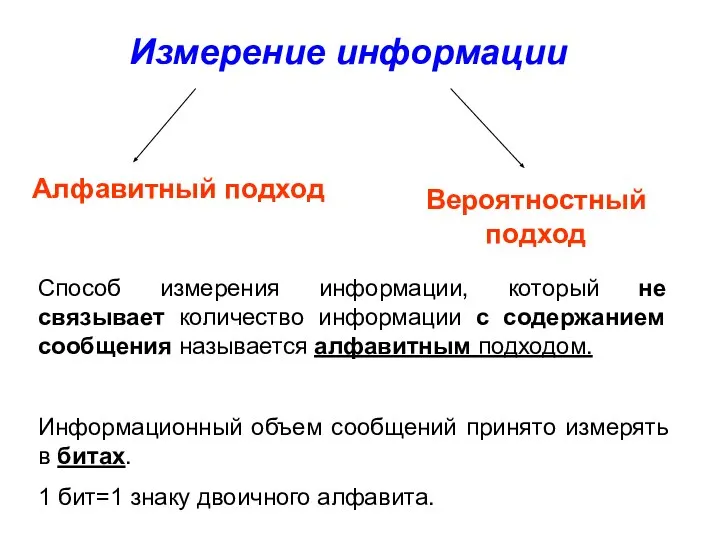 Измерение информации
Измерение информации Элементы алгебры логики
Элементы алгебры логики Electronic presentation of the University
Electronic presentation of the University Основы алгоритмизации и программирования. Итоги тестовой работы №4
Основы алгоритмизации и программирования. Итоги тестовой работы №4 7-1-5 (1)
7-1-5 (1) Linux now and forever
Linux now and forever Мир нанотехнологий. Игра
Мир нанотехнологий. Игра Домашнее (условие фано)
Домашнее (условие фано) Операционные системы
Операционные системы