Содержание
- 2. В наше время современному человеку постоянно попадаются числа, цифры… они с нами везде. А 2 тысячи
- 3. От положения знака в изображении числа не зависит величина, которую он обозначает. Система счисления непозиционная позиционная
- 4. В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает.
- 5. Он был итальянским математиком. Благодаря его книге «Liber Abaci» Европа узнала индо-арабскую систему чисел, которая позднее
- 6. Позиционную систему счисления называют традиционной, если ее базис образует члены геометрической прогрессии, а значения цифр есть
- 7. Система счисления или нумерация- это способ записи чисел. Символы, при помощи которых записываются числа, называются цифрами,
- 8. Где А-само число, q-основание системы счисления, а-цифры данной системы счисления, n-число разрядов целой части числа, m-число
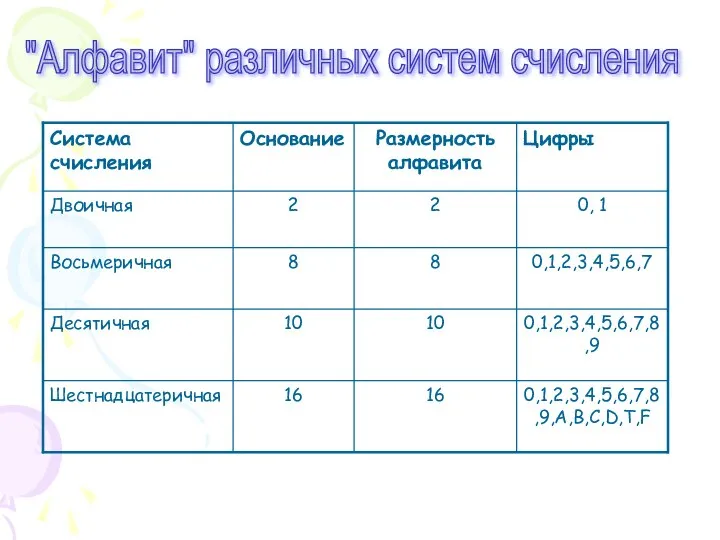
- 9. "Алфавит" различных систем счисления
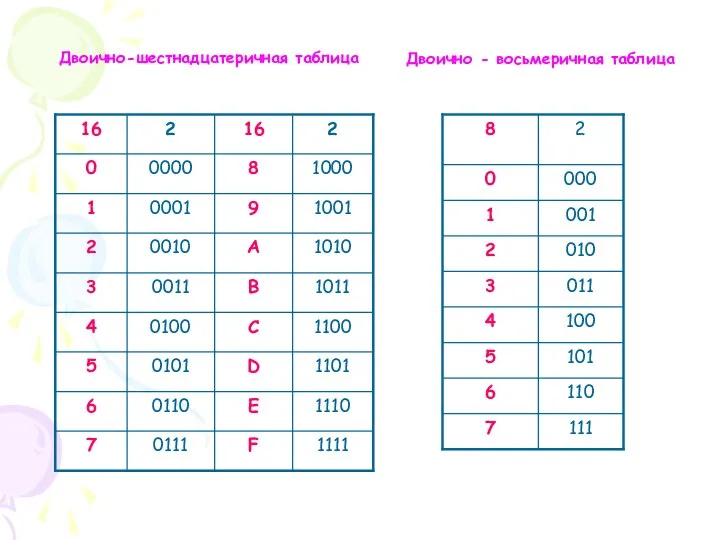
- 10. Двоично-шестнадцатеричная таблица Двоично - восьмеричная таблица
- 11. 315 24 75 72 3 8 32 7 8 4 315 16 9 16 155 144
- 12. 3750 5000 0000 0 1 х 2 0 1875 7500 1 0 х 2 х 2
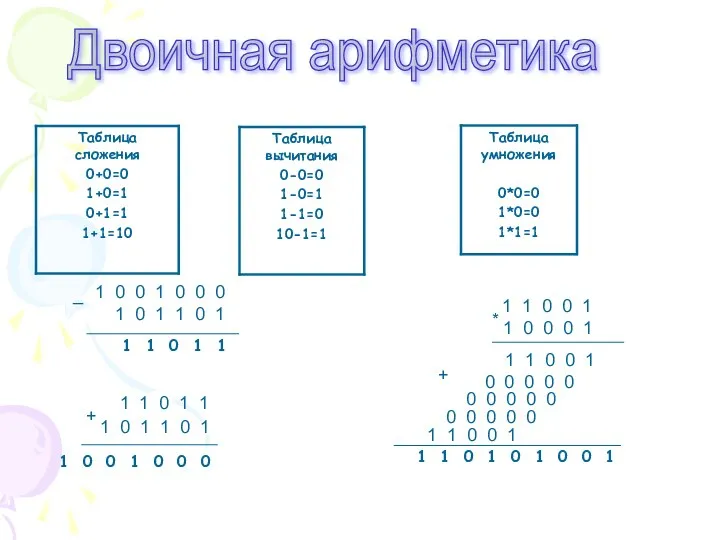
- 13. Двоичная арифметика 1 1 0 1 1 1 0 1 1 0 1 1 0 0
- 14. Ей было 1100 лет. Она в 101 класс ходила. В портфеле по 100 книг носила. Все
- 16. Скачать презентацию









 Инструкция по порталу Госуслуг
Инструкция по порталу Госуслуг Применение программы Packet Tracer при изучение принципов работы Wi-Fi роутера
Применение программы Packet Tracer при изучение принципов работы Wi-Fi роутера Классификация языков программирования. Структура программы на С#. Первая программа
Классификация языков программирования. Структура программы на С#. Первая программа Презентация на тему Информационные модели (7 класс)
Презентация на тему Информационные модели (7 класс)  Microsoft Power Point. Упражнения по анимации объектов, выполненных из автофигур
Microsoft Power Point. Упражнения по анимации объектов, выполненных из автофигур Проработка и тестирование по теме Access
Проработка и тестирование по теме Access Лаборатория онлайн бизнеса 2021
Лаборатория онлайн бизнеса 2021 Что называют архитектурой? Что понимается под устройством компьютера?
Что называют архитектурой? Что понимается под устройством компьютера? Понятие алгоритма. Примеры алгоритмов из окружающей жизни
Понятие алгоритма. Примеры алгоритмов из окружающей жизни Проблемы передачи информации (лекция 3)
Проблемы передачи информации (лекция 3) Количественная характеристика информации
Количественная характеристика информации HTML – Hypertext Markup Language
HTML – Hypertext Markup Language Реляционная модель данных
Реляционная модель данных Операционные системы
Операционные системы Помощь студенту к первой лабораторной работе. При выполнении лабораторных работ используется программа ISE Project Navigator
Помощь студенту к первой лабораторной работе. При выполнении лабораторных работ используется программа ISE Project Navigator Моё имя. 1 класс
Моё имя. 1 класс Инструкция. Создание карточки дворника. Закрепление за объектами
Инструкция. Создание карточки дворника. Закрепление за объектами Формирование информационной грамотности через работу с текстом на уроках окружающего мира
Формирование информационной грамотности через работу с текстом на уроках окружающего мира MagicDom. Game
MagicDom. Game Solidworks как мощное средство проектирования, ядро интегрированного комплекса автоматизации предприятия
Solidworks как мощное средство проектирования, ядро интегрированного комплекса автоматизации предприятия Цикл с условием окончания работы
Цикл с условием окончания работы Материал о шрифтах, их видах и способах выполнения
Материал о шрифтах, их видах и способах выполнения Урок 9. Файловая система (дз)
Урок 9. Файловая система (дз) Маршрутизация и транспортировка данных по компьютерным сетям
Маршрутизация и транспортировка данных по компьютерным сетям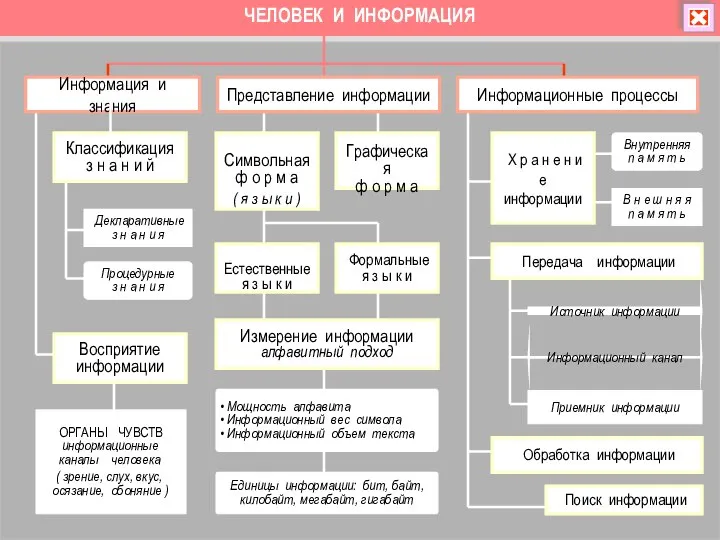 Человек и информация. Информация и знания
Человек и информация. Информация и знания Носители_информации
Носители_информации Как работает поисковая машина
Как работает поисковая машина Програмування мовою С/C++
Програмування мовою С/C++