Системы счисления

ЦЕЛЬ: Ознакомить учащихся с одним из разделов школьного курса информатики историей развития и классификацией различных систем счисления, с алгоритмом перевода из десятичной системы счисления в другие(двоичная, восьмеричная, шестнадцатеричная).
Используемые информационные продукты:
Microsoft Power Point - для создание и демонстрации презентации;
Microsoft Word - для набора текста;
Paint - для создания графических объектов;
Adobe Photoshop - для редактирования графических объектов;
Системные требования:
Презентацию можно выполнить на компьютере любого класса где содержаться Win98/ME/2000/XP
Программа Microsoft Power Point любой версии.
Особых ограничений НЕТ.
Содержание проекта:
Основные темы:
История системы счисления
Непозиционные системы счисления
Позиционные системы счисления
Двоичная арифметика
Алгоритм перевода чисел из одной системы счисления в другую

Представление числовой информации
с помощью систем счисления
ЧЕМ ОТЛИЧАЕТСЯ ЦИФРА ОТ ЧИСЛА?
Для записи информации о количестве объектов используются числа.
Числа записываются с использованием особых знаковых систем, которые называются системами счисления.
Знаки системы счисления, с помощью которых записывают числа – это цифры.
ЦИФР ОГРАНИЧЕННОЕ КОЛИЧЕСТВО,
А ЧИСЕЛ БЕСКОНЕЧНО МНОГО!

В древние времена, когда люди начали считать, появилась потребность в записи чисел.
Количество предметов изображалось нанесением равного количества черточек, зарубок или засечек на какой-либо твердой поверхности.
Унарная система счисления
Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.
Раскопки относятся к периоду палеолита (10–11 тысяч лет до н.э.)

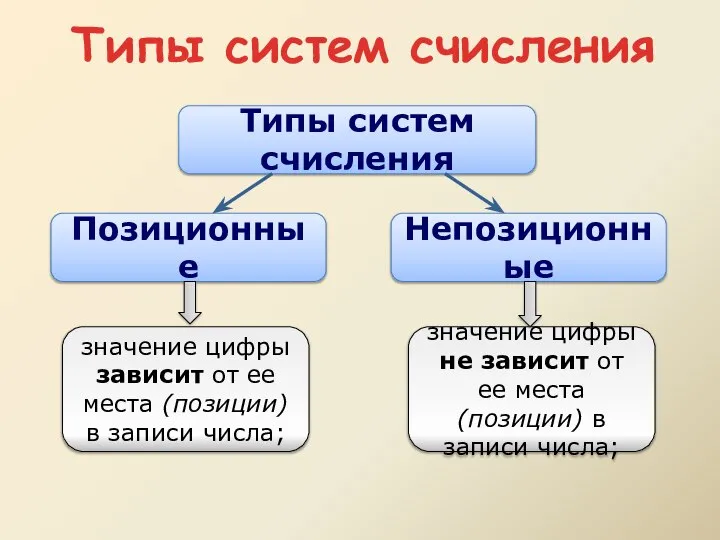
Типы систем счисления

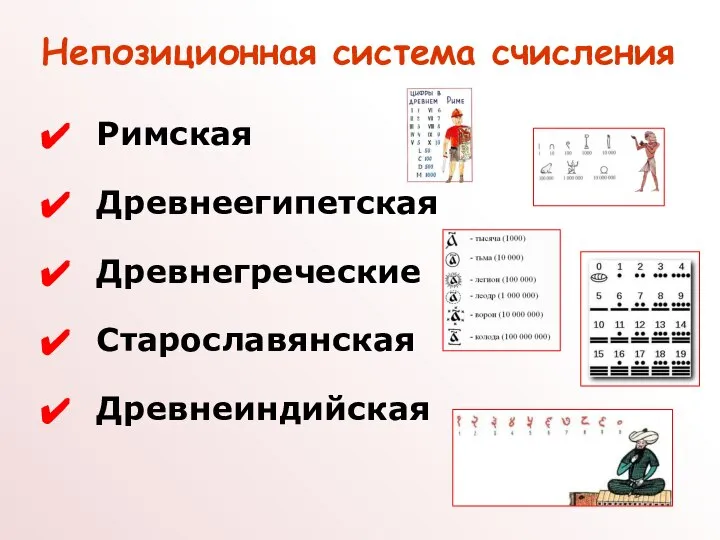
Римская
Древнеегипетская
Древнегреческие
Старославянская
Древнеиндийская
Непозиционная система счисления

Древнеегипетская система счисления
Возникла во второй половине III тысячелетия до н.э.
Каждый символ повторяется определенное число раз, и, чтобы прочитать число, нужно просуммировать значения всех символов, входящих в его запись.

Древнегреческая система счисления
Древнегреческая аттическая пятеричная
В древнейшее время в Греции была распространена так называемая Аттическая система счисления, название происходит от области Греции– Аттики со столицей Афины.

Славянская система счисления
= 800+60+3 = 863
Использовалась она нечасто, но достаточно долго.
По организации повторяет греческую нумерацию. Использовалась она с VIII по XIII в.
Алфавитная система была принята и в Древней Руси. Получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел.
Была создана для перевода священных библейских книг для славян греческими монахами братьями Кириллом и Мефодием в IX веке.

Славянская система счисления
Славянская кириллическая десятеричная алфавитная

Римская непозиционная СС
(500 лет до н.э.) Используется обозначение веков, номера глав в книгах, циферблат часов
Для записи чисел используются буквы латинского алфавита

Римская непозиционная СС
если меньшая цифра стоит слева от большей
IX (10-1=9)
если меньшие цифры стоят справа от большей
XII (10+1+1=12)
не ставят больше трех одинаковых цифр подряд
Примеры:
–
+
D X L I I
= 542
X X X I I
= 32
98 = XCVIII
99 = XCIX
100 = C
101 = CI
102 = CII
97 = XCVII

Римская непозиционная СС
=1000+(500-100)+(50+10)+(5-1)= 1464
= 1000 + 200 + 70 + 9 = MCCLXXIX
M
CC
LXX
IX
1279
MCDLXIV
Переведите числа в римскую СС и обратно.

Задание № 1
CMXVII =
MMCXXIX=
MCMLXIII =
405 =
1984 =
2983 =

Недостатки непозиционных СС
Существует постоянная потребность введения новых знаков для записи больших чисел.
Невозможно представлять дробные и отрицательные числа.
Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения.

Позиционные системы счисления
Позиционная система - значение цифры определяется ее позицией в записи числа.
Десятичная
Вавилонская (шестидесятиричная)
Племена индейцев Майя
(двадцатеричная)
Двенадцатеричная (древняя Шумера)
В компьютерной технике (двоичная, восьмеричная, шестнадцатеричная)

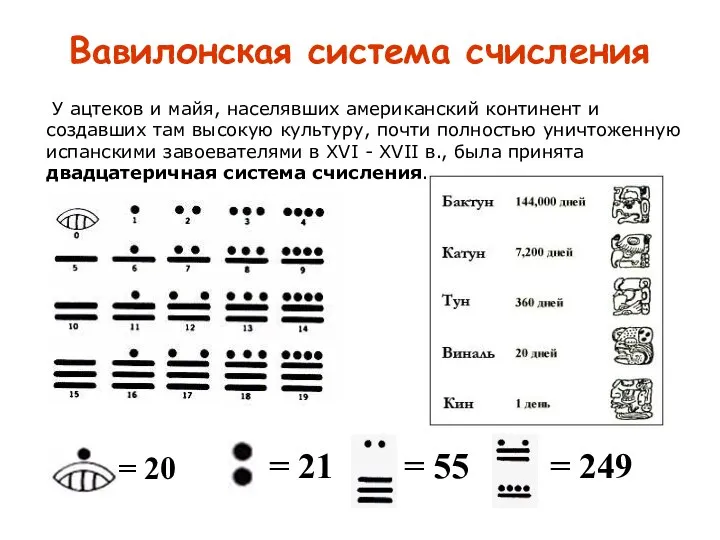
Шестидесятеричная вавилонская система – первая известная система счисления, основанная на позиционном принципе.
Числа менее 60 обозначались с помощью двух знаков:
прямой клин служил для обозначения единиц, лежачий клин – для обозначения десятков.
- единицы
- десятки
Вавилонская система счисления
- ноль
Древний Вавилон
(II тысячелетие до нашей эры)

Вавилонская система счисления
= 20
= 21
= 55
= 249
У ацтеков и майя, населявших американский континент и создавших там высокую культуру, почти полностью уничтоженную испанскими завоевателями в XVI - XVII в., была принята двадцатеричная система счисления.

Арабская нумерация
400 г. н.э – изобретена в Индии
800 г.н.э. – заимствована арабами
в 1200 г.н.э. - начали применять в Европе,
В Европе они стали известны благодаря трудам арабских математиков, и потому за ними утвердилось название «арабские», хотя сами арабы вплоть до настоящего времени пользуются совсем другими символами.
Арабские цифры:
В России арабская нумерация стала использоваться при Петре I (до конца XVII века сохранилась славянская нумерация)
Самая распространенная на сегодняшний день нумерация, которой мы пользуемся в настоящее время.
0 1 2 3 4 5 6 7 8 9

Наиболее распространенными
в настоящее время являются :
-десятичная
-двоичная
-восьмеричная
-шестнадцатеричная
позиционные системы счисления.

Любое число мы можем записать при помощи десяти цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Именно поэтому наша современная система счисления называется десятичной.
Известный русский математик Н.Н.Лузин так выразился по этому поводу:
«Преимущества десятичной системы счисления не
математические, а зоологические. Если бы у нас было на
руках не десять пальцев, а восемь, то человечество бы
пользовалось восьмеричной системой счисления.»
Десятичная система счисления

Была придумана задолго до появления компьютеров. Официальное рождение двоичной арифметики связано с именем Г. В. Лейбница, опубликовавшего в 1703 г. статью, в которой он рассмотрел правила выполнения арифметических действий над двоичными числами. Ее недостаток – «длинная» запись чисел.
В настоящий момент – наиболее употребительная в информатике, вычислительной технике и смежных отраслях система счисления. Использует две цифры: 0 и 1
Пример:
Свернутая форма записи числа: 1012
2 1 0
Развернутая форма: 101 =1*22 +0*21+1*20
Все числа в компьютере представляются
с помощью нулей и единиц, т. е.
в двоичной системе счисления.
Двоичная система счисления

где А-само число,
q-основание системы счисления,
а- цифры данной системы счисления,
n-число разрядов целой части числа,
m-число разрядов дробной части числа.
Пример:
Развернутая форма записи числа
единицы
десятки
сотни
тысячи

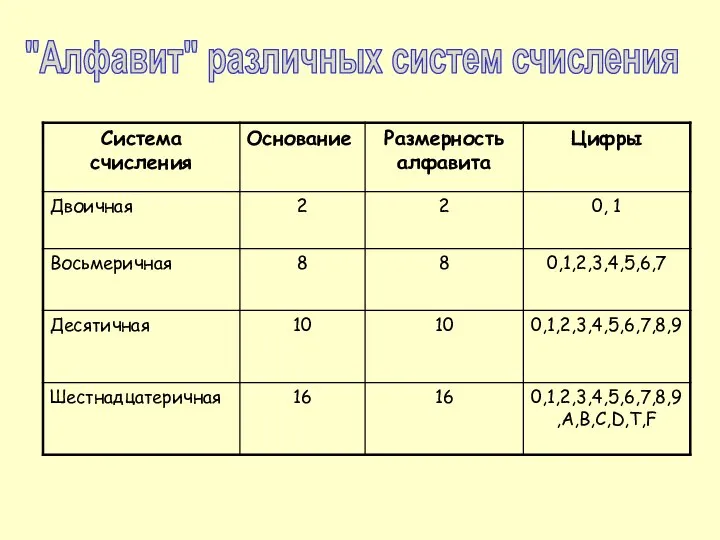
"Алфавит" различных систем счисления

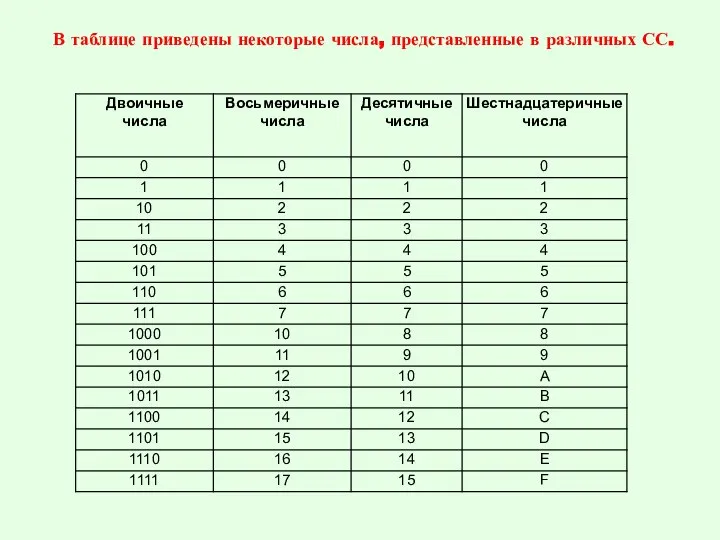
В таблице приведены некоторые числа, представленные в различных СС.

Перевод чисел в десятичную с/с
Алгоритм перевода:
1. Представьте число в развернутой форме. При этом основание с/с должно быть представлено в десятичной системе счисления.
2. Найдите сумму ряда. Полученное число является значением числа в десятичной
системе счисления.
Примеры:
Переведем число 110012 в десятичную систему счисления.
1. Запишем число в развернутой форме:
11012 = 1⋅24+1⋅23 + 0⋅22 + 0⋅21 + 1⋅20.
2. Найдем сумму ряда: 24+23+0+0+20 = 16+8+4+1 = 2910.
Переведем число 16,48.
1. Запишем число в развернутой форме: 1⋅81+6⋅80+4⋅8-1
2. Найдем сумму: 8+6+0,5 = 14,510.

Задание № 2

Перевод чисел из десятичной с/с в двоичную
Алгоритм перевода целых чисел из десятичной системы счисления в любую другую:
1. Последовательно выполнить деление данного числа и получаемых целых частных на основание новой с/с, пока не получится частное, меньшее делителя.
2. Полученные остатки являются цифрами числа в новой с/с.
3. Составить число в новой системе счисления, записывая его
начиная с последнего остатка.

315
24
75
72
3
8
32
7
8
4
315
16
9
16
155
144
11
(В)
16
3
16
1
15
2
2
2
14
1
7
6
1
3
2
1
1
Перевод десятичных чисел в другие
Двоичная
Восьмеричная
Шестнадцатеричная
39
1

3750
5000
0000
0
1
х 2
0
1875
7500
1
0
х 2
х 2
х 2
0
1875
0000
х 16
3
Перевод десятичной дроби
0
1875
0000
1
х 8
х 8
4
5000
Двоичная
Восьмеричная
Шестнадцатеричная

Задание № 3

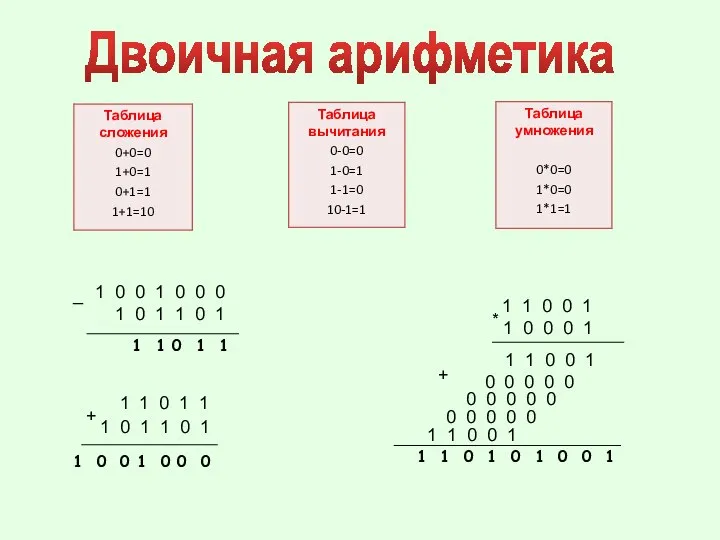
Двоичная арифметика
1 1 0 1 1
1 0 1 1 0 1
1 0 0 1 0 0 0
+
1 0 0 1 0 0 0
1 0 1 1 0 1
1 1 0 1 1
_
1 1 0 0 1
1 0 0 0 1
*
1 1 0 0 1
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
1 1 0 0 1
+
1 1 0 1 0 1 0 0 1

Ей было 1100 лет.
Она в 101 класс ходила.
В портфеле по 100 книг носила.
Все это правда, а не бред.
Когда пыля десятком ног.
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий,
Она ловила каждый звук
Своими десятью ушами,
И 10 загорелых рук
Портфель и поводок держали.
И 10 темно-синих глаз
Оглядывали мир привычно.
Но станет все совсем обычным,
Когда поймете наш рассказ.
Задача

ОТВЕТ
Ей было 12 лет.
Она в 5 класс ходила.
В портфеле по 4 книг носила.
Все это правда, а не бред.
Когда пыля десятком ног.
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий,
Она ловила каждый звук
Своими десятью ушами,
И 2 загорелых рук
Портфель и поводок держали.
И 2 темно-синих глаз
Оглядывали мир привычно.
Но станет все совсем обычным,
Когда поймете наш рассказ.

Задание № 4
1. Выполните арифметические операции в двоичной системе счисления:
а) 1110 + 1001
б) 101,101 + 11,01
в) 10101 + 1111
г) 1011011 + 101010
д) 1010 + 1111
е) 1110 - 1001
ж) 10101 – 110
з) 1000011 – 101
и) 10101 – 1010
к) 1100 – 11
л) 1110 × 1001
м) 1101 × 101
н) 101,1 × 11,1
о) 1001,01 × 11
п) 10011 × 111
2. Решите задачи в двоичной системе счисления.
а) На берегу моря лежало 10 камешков. Набежавшая волна выбросила еще несколько. Их стало 1000. Сколько камешков было выброшено волной?
б) Греются на солнышке воробьи. На нижней ветке их было 110, на верхней – на 10 меньше. Сколько всего было воробьев?
в) Младший брат учится в 101 классе. Старший на 11 лет старше. В каком классе учится старший брат?
г) В кабинетах биологии и информатики 1010 кактусов. В биологии их 111. Сколько кактусов в кабинете информатики?
д) У первоклассника Миши 1111 палочек для счета. У Коли 101. На сколько палочек у Миши больше, чем у Коли?