Слайд 2Системой счисления называют определенные правила записи чисел и связанные с ними способы
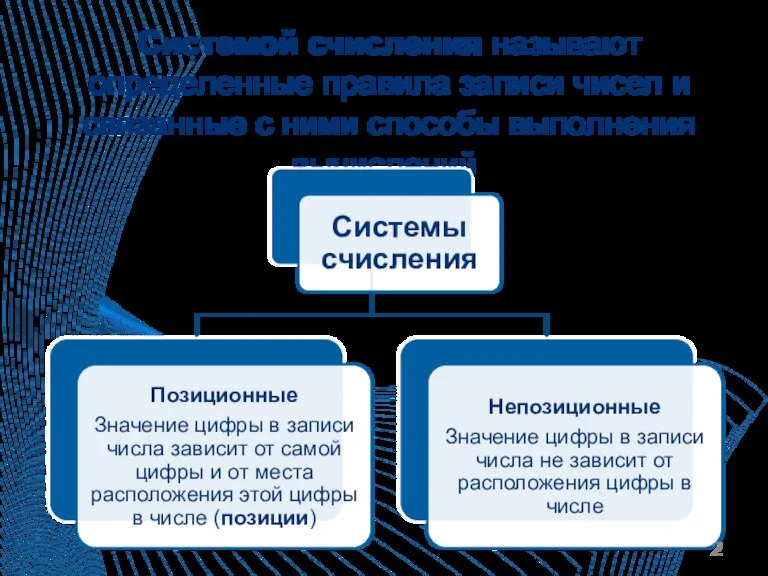
выполнения вычислений.
Слайд 3Примеры систем счисления
Позиционные: десятичная, двоичная, троичная….
Непозиционные: римская…

Слайд 4Компьютер работает с числами в двоичной системе счисления.
Эта идея принадлежит Джону фон

Нейману, сформулировавшему в 1946 году принципы устройства и работы ЭВМ.
Слайд 5Десятичная система счисления
Система счисления называется десятичной потому ,что для записи любого числа

в ней используются десять цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Число цифр определяет основание системы счисления.
В десятичной системе счисления основание равно десяти.
Слайд 6Двоичная система счисления
Система счисления называется двоичной, потому что для записи любого числа

в ней используются две цифры:
0, 1.
В двоичной системе счисления основание равно двум.
Слайд 7Развернутая форма записи числа
В позиционных системах счисления значение цифры в записи числа

зависит не только от самой цифры, но и от места расположения этой цифры в числе.
Например в числе 333 первая справа цифра обозначает три единицы, следующая — три десятка, следующая — три сотни. Этот факт можно выразить равенством:
33310 = 3 • 102 + 3 • 101 + 3 • 10° = 300 + 30 + 3.
Выражение, стоящее справа от знака «равно», называется развернутой формой записи многозначного числа.
Слайд 8Задание.
Запишите число в развернутой форме:
Основание системы 10
3210
8257
=8•103 + 2•102 + 5•101

+ 7•100
= 8000 + 200 + 50 + 7
Слайд 9Перевод двоичной системы счисления чисел в десятичную
Задание: перевести число 1101012, записанное в

двоичной системе счисления в десятичную.
Для выполнения задания необходимо записать это число в развернутой форме:
1101012 = 1•25 + 1•24 + 0•23 + 1•22 + 0•21 + 1•20 = 5310
Слайд 10Соответствие записи чисел в десятичной и двоичной системе счисления:

Слайд 11Задание
Переведите числа из двоичной системы счисления в десятичную:
1000001=
10000001=
100000001=
1000000001=

Слайд 12Перевод десятичных чисел в двоичную систему
Перевод осуществляется при помощи деления десятичного числа
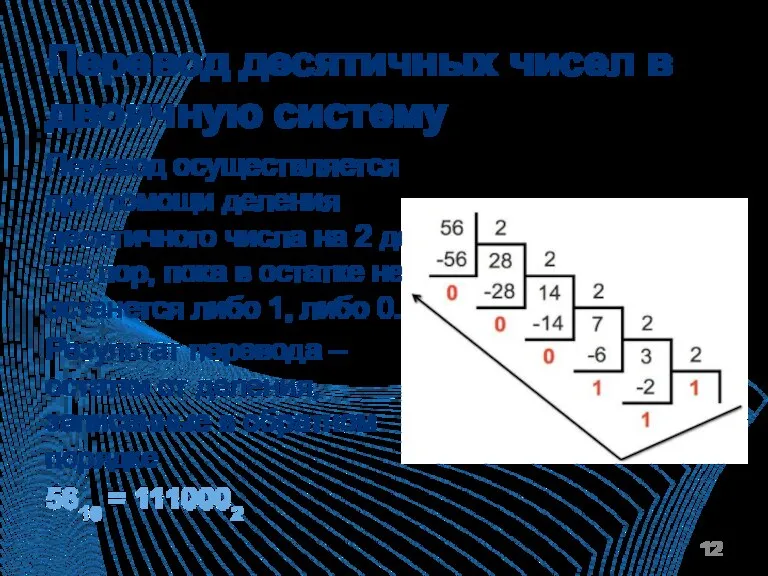
на 2 до тех пор, пока в остатке не останется либо 1, либо 0.
Результат перевода – остатки от деления, записанные в обратном порядке
5610 = 1110002
Слайд 13Задание
Переведите в двоичную систему счисления следующие десятичные числа:
2
7
17

68
315
765
2047
Слайд 14Правила перевода в другие позиционные системы счисления
Перевод чисел из других систем счисления

в десятичную и наоборот из десятичной в другие системы счисления осуществляется аналогичным образом.
Изменяется только основание необходимой системы счисления
Слайд 15Алгоритм перевода дробных чисел из 10 системы в двоичную
Перевод целой части:
Целая и

дробная часть числа переводится отдельно.
В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой.
Алгоритм перевода целой части был приведен выше.
Слайд 16Алгоритм перевода дробных чисел из 10 системы в двоичную
Перевод дробной части:
Необходимо последовательно

умножать дробную часть числа на основание новой системы до тех пор, пока дробная часть не станет равна нулю;
Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления привести в соответствие с алфавитом новой системы счисления;
Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Слайд 17Задание:
Переведите число 315,1875 из десятичной в двоичную систему счисления
Переведите 31510 =
Переведите

0,187510=
Запишите результат
100111011,0011
Слайд 18Задание:
Переведите число 315,1875 из десятеричной в восьмеричную систему счисления
473,148

Слайд 19Задание:
Переведите числа из десятичной системы в двоичную и восьмеричную
40,5
34,25
124,44
78,333
225,52

Слайд 20Перевод дробных чисел из двоичной системы в десятичную

Слайд 21Задание:
Переведите из двоичной системы в десятичную
1101,11
11,00111
11011,11
1100110,111

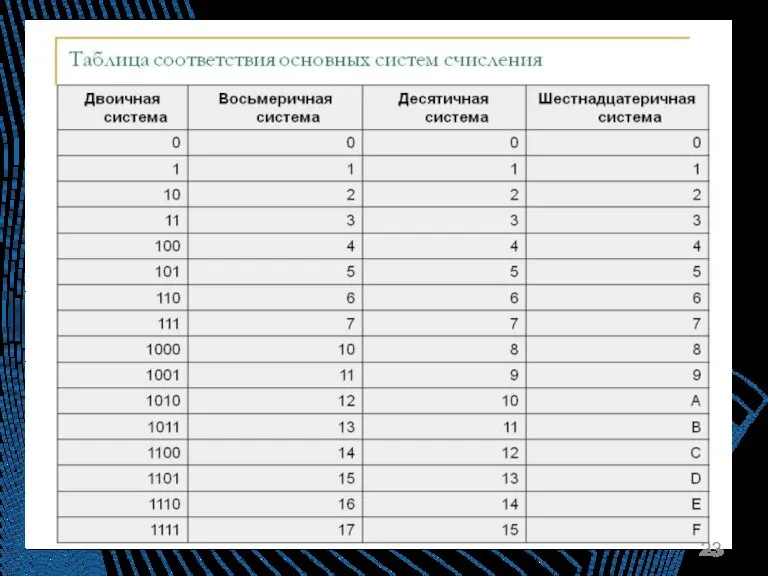
Слайд 24Для перевода чисел из одной системы в другую необходимо знать таблицы:
Двоично-восьмеричная

Слайд 25Для перевода чисел из одной системы в другую необходимо знать таблицы:
Двоично-шестнадцатеричная

Слайд 26Алгоритм перевода целых чисел из
двоичной системы счисления в восьмеричную и шестнадцатеричную
Двоичное

число разбить группы по n цифр в каждой, начиная справа (восьмеричная система – 3 цифры, шестнадцатеричная система – 4 цифры).
Если в последней группе окажется меньше n разрядов, то ее необходимо дополнить нулями.
Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в необходимой системе счисления.
Слайд 27Задание
11 0111 1010 1110 1111
1111
1110
1010
0111
0011
3
7
A
E
F
37AEF
Перевести двоичное число в шестнадцатеричную систему

Слайд 28Алгоритм перевода целых чисел из
восьмеричной и шестнадцатеричной систем счисления в двоичную
Связь

между двоичной и восьмеричной системой устанавливается аналогично.
В этом случае используется двоично-восьмеричная таблица.
Каждой восьмеричной цифре соответствует тройка двоичных цифр.
Слайд 29Задание
15FC
0001
0101
1111
1100
1010111111100
Перевести число из шестнадцатеричной системы в двоичную

Слайд 30Задание
Перевести двоичные числа в восьмеричную систему
110000110101
1010101

Слайд 31Задание:
Перевести двоичные числа в шестнадцатеричную систему
11011010001
11111111100001

Слайд 32Задание
Перевести восьмеричные числа в двоичную систему
256
657

Слайд 33Задание
Перевести шестнадцатеричные числа в двоичную систему
1AC7
FACC

Слайд 34Алгоритм перевода дробных чисел:
Целая и дробная части разбиваются на группы по n

цифр в каждой.
Если в целой и дробной части окажется меньше цифр для деления на группы, необходимо дополнить справа и слева эти части нулями.
Рассмотреть каждую часть как n-разрядное двоичное число и записать ее соответствующей цифрой в необходимой системе счисления.
Записать через запятую обе части.
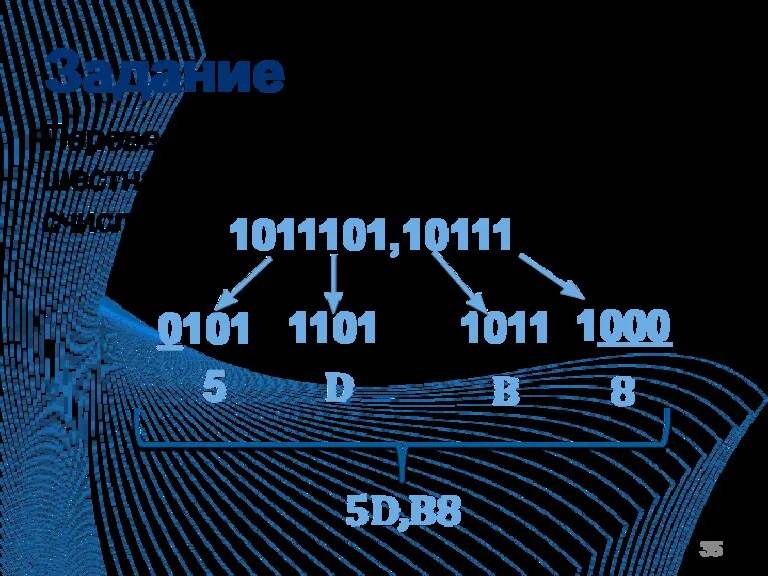
Слайд 35Задание
1011101,10111
1000
1011
1101
0101
5
B
8
D
5D,B8
Перевести число в шестнадцатеричную систему счисления
Слайд 36Задание
Перевести числа из двоичной в шестнадцатеричную и восьмеричную системы счисления
1100010,011101
1111000000,101
101010,111001

Слайд 37Перевод из восьмеричной системы в шестнадцатеричную и наоборот
Каждую восьмеричную (шестнадцатеричную) цифру надо

перевести в двоичный вид и представить тремя (четырьмя) разрядами двоичного числа в соответствии с таблицей
Записать код числа в соответствии с таблицей
Слайд 38Арифметика двоичных чисел
Возможные варианты сложения и умножения двоичных чисел:
0+0=0 0x0=0
0+1=1 0x1=0
1+0=1 1x0=0
1 + 1 =

10 1x1 = 1
Слайд 40Задание
1. Перевести целые числа из десятичной системы в троичную
523
65
7000
2. Перевести целые числа

из десятичной системы в восьмеричную
856
664
5012
Слайд 41Задание
3. Перевести десятичные дроби в двоичную систему счисления. В двоичной записи числа

сохранить 5 знаков
225, 52
78,333
90,99
Слайд 42Задание
4. Перевести смешанные двоичные числа в восьмеричную и шестнадцатеричную системы
101111,01100
100000111,001110
101010,0010

Слайд 43Задание
5. Перевести числа из шестнадцатеричной в двоичную систему счисления
FACC
A24,F9
21D,567










































 Программное обеспечение и его классификация
Программное обеспечение и его классификация Cпособы обтравки изображений
Cпособы обтравки изображений Национальная электронная библиотека (НЭБ)
Национальная электронная библиотека (НЭБ) Lesson 4
Lesson 4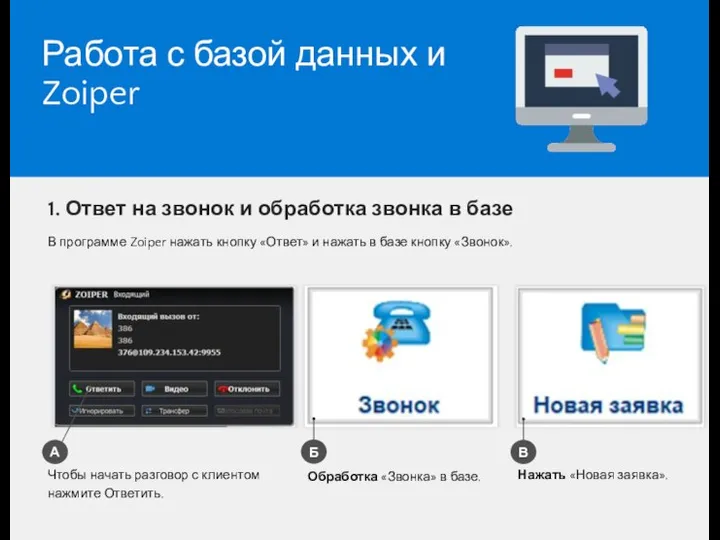 Работа с базой данных и Zoiper
Работа с базой данных и Zoiper Общие сведения о языке программирования Паскаль. Начала программирования
Общие сведения о языке программирования Паскаль. Начала программирования Интернет. Введение
Интернет. Введение Ведение страницы ТОДЮБ в социальных сетях, полезные советы
Ведение страницы ТОДЮБ в социальных сетях, полезные советы Навигационная система дополненной реальности в современных системах
Навигационная система дополненной реальности в современных системах Метрология и теория измерений
Метрология и теория измерений Создать БД Видеосалон
Создать БД Видеосалон Как нарисовать шахматную доску?
Как нарисовать шахматную доску? Кроссворд ко дню библиотекаря
Кроссворд ко дню библиотекаря Електронні таблиці MS Excel
Електронні таблиці MS Excel Технология обработки числовой информации. Электронные таблицы MS Excel. Основные приёмы работы
Технология обработки числовой информации. Электронные таблицы MS Excel. Основные приёмы работы Протокол IPv6. Вычислительные сети и коммуникации
Протокол IPv6. Вычислительные сети и коммуникации Качество кода
Качество кода Основы PowerShell
Основы PowerShell Money back from fake. Достоверная информация
Money back from fake. Достоверная информация Знакомство с интерфейсом OpenOffice.org Calc
Знакомство с интерфейсом OpenOffice.org Calc Средства анализа и визуализации данных
Средства анализа и визуализации данных Аналізування відеоповідомлень
Аналізування відеоповідомлень Компьютерное моделирование/ Геофизика
Компьютерное моделирование/ Геофизика Инструменты графического редактора Paint
Инструменты графического редактора Paint Построение диаграмм
Построение диаграмм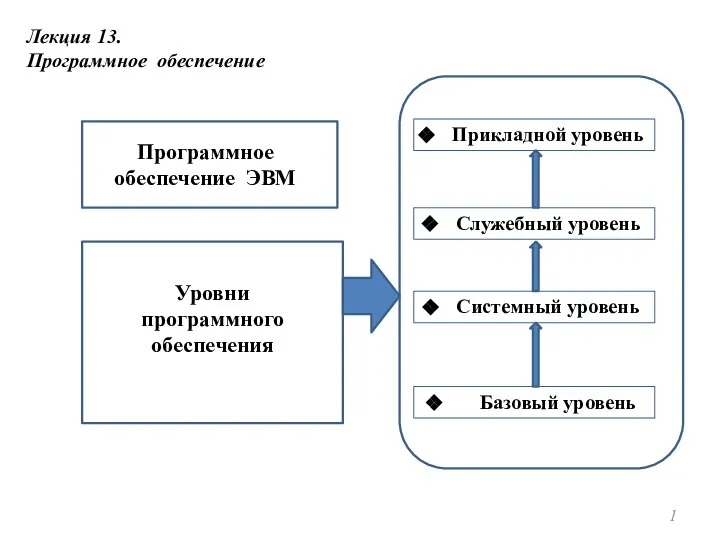 Программное обеспечение
Программное обеспечение Поиск рабочего оффера и поставщика
Поиск рабочего оффера и поставщика База данных
База данных