Структуры данных: стеки, деки, очереди

Полустатические структуры данных
Полустатические структуры данных характеризуются следующими признаками:
они имеют переменную длину и простые процедуры ее изменения;
изменение длины структуры происходит в определенных пределах, не превышая какого-то максимального (предельного) значения.
Если полустатическую структуру рассматривать на логическом уровне, то о ней можно сказать, что это последовательность данных, связанная отношениями линейного списка. Доступ к элементу может осуществляться по его порядковому номеру.
Физическое представление полустатических структур данных в памяти - это обычно последовательность слотов в памяти, где каждый следующий элемент расположен в памяти в следующем слоте (т.е. вектор). Физическое представление может иметь также вид однонаправленного связного списка (цепочки), где каждый следующий элемент адресуется указателем находящемся в текущем элементе. В последнем случае ограничения на длину структуры гораздо менее строгие.

Стек - такой последовательный список с переменной длиной, включение и исключение элементов из которого выполняются только с одной стороны списка, называемого вершиной стека.

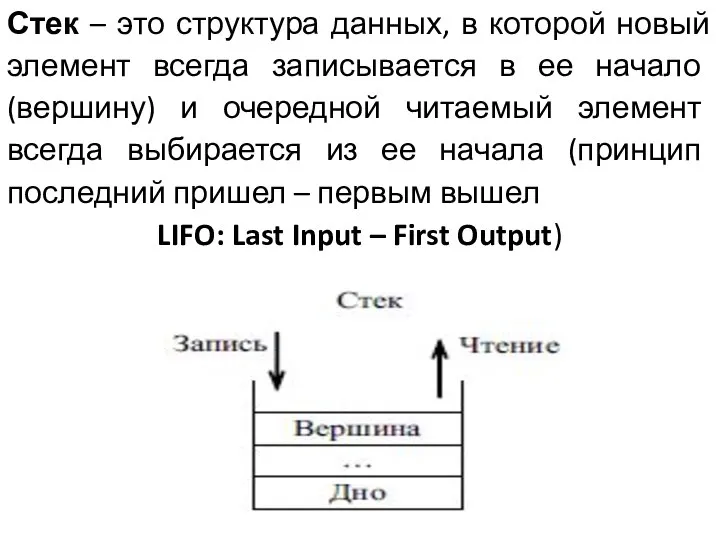
Стек – это структура данных, в которой новый элемент всегда записывается в ее начало (вершину) и очередной читаемый элемент всегда выбирается из ее начала (принцип последний пришел – первым вышел
LIFO: Last Input – First Output)

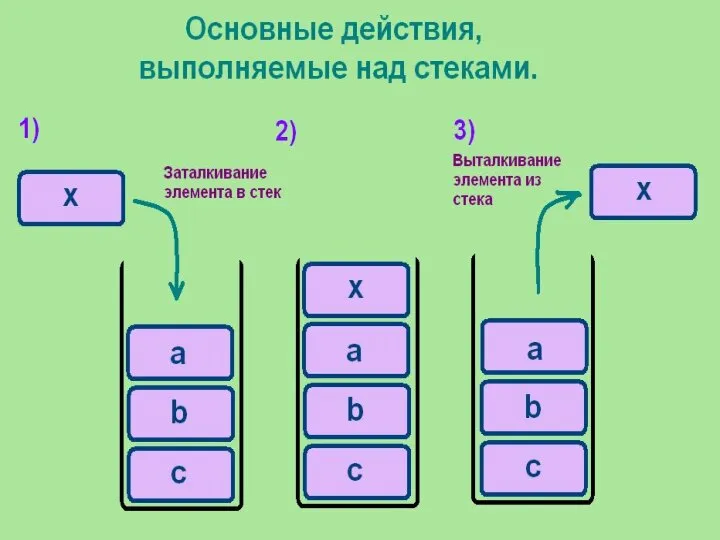
Операции, производимые над стеком
включение нового элемента (английское название push - заталкивать);
исключение элемента из стека (англ. pop - выскакивать).
чтение элемента из стека (может быть реализовано, как комбинация операций: x:=pop(stack); push(stack,x));
очистка стека;
проверка пустоты стека;
определение текущего числа элементов в стеке.

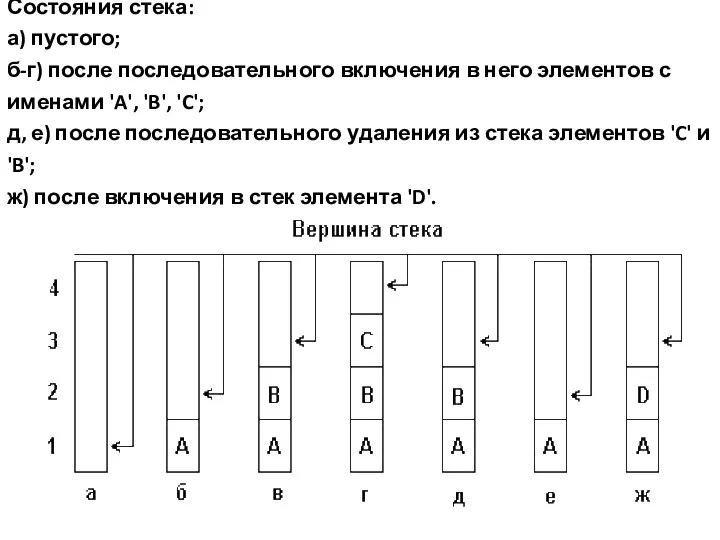
Состояния стека:
а) пустого;
б-г) после последовательного включения в него элементов с именами 'A', 'B', 'C';
д, е) после последовательного удаления из стека элементов 'C' и 'B';
ж) после включения в стек элемента 'D'.

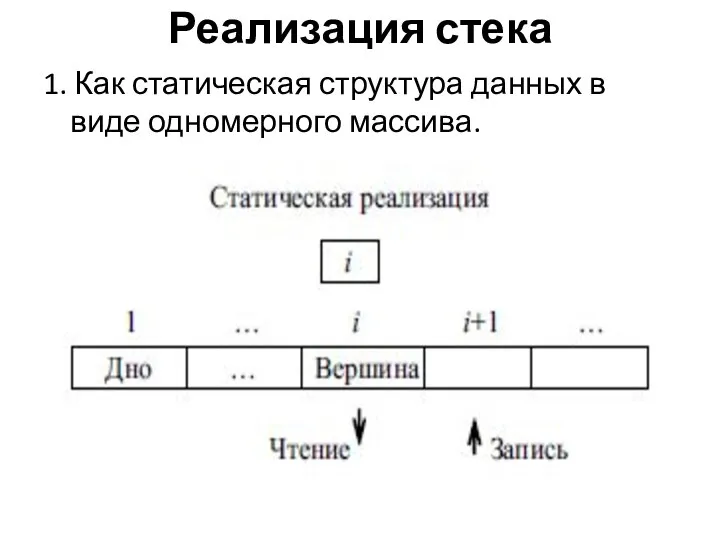
Реализация стека
1. Как статическая структура данных в виде одномерного массива.

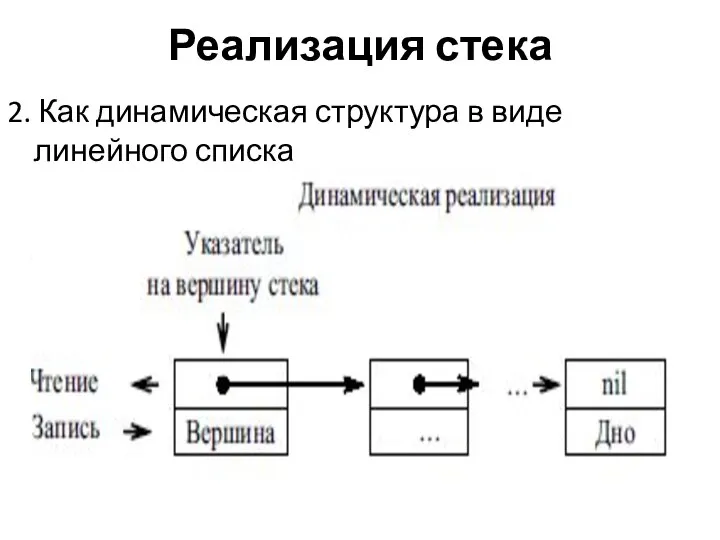
Реализация стека
2. Как динамическая структура в виде линейного списка

Работа со стеком на базе массива
Работаем с элементами типа elem.
Type elem = <тип элемента стека>;
stack=array[1..100] of elem;
Определить глубину стека величиной n. Будем считать, сто стек пуст при n=0.

Описание процедур работы со стеками
Добавление элемента в стек
Procedure push (var n:integer; X: elem; Var s: stack);
Begin
n:= n + 1;
S[n]:= x;
End;

Описание процедур работы со стеками
Извлечение элемента из стека
Procedure pop (var n:integer; X: elem; Var s: stack);
Begin
x:= S[n];
n:= n -1;
End;

Работа со стеком на основе линейного списка
type PElement = ^TypeElement; {указатель на тип элемента}
TypeElement = record {тип элемента списка}
Data: TypeData; {поле данных элемента}
Next: PElement; {поле указателя на следующий элемент}
end;
var ptrHead: PElement; {указатель на первый элемент списка}
ptrCurrent: PElement; {указатель на текущий элемент}

Запись элемента в стек
procedure PushStack(NewElem: TypeData;
var ptrStack: PElement);
begin
InsFirst_LineSingleList(NewElem, ptrStack);
end;

Чтение элемента из стека
procedure PopStack(var NewElem: TypeData, ptrStack: PElement);
Begin
if ptrStack <> nil then
begin
NewElem := ptrStack^.Data; Del_LineSingleList(ptrStack, ptrStack);
end;
end;

Очистка стека
procedure ClearStack(var ptrStack: PElement);
begin
while ptrStack <> nil do Del_LineSingleList(ptrStack, ptrStack);
end;

Проверка пустоты стека
function EmptyStack(var ptrStack:PElement): boolean;
begin
if ptrStack = nil then EmptyStack := true
else EmptyStack := false;
end;

Задание для самостоятельной работы
Рассмотреть процедуры :
вставки первого элемента списка
InsFirst_LineSingleList;
вставки последующих элементов списка
Ins_LineSingleList;
удаление вершины стека
Del_LineSingleList(ptrStack, ptrStack);
Литература:
1. Ключарев А.А., Матьяш В.А., Щекин С.В. Структуры и алгоритмы обработки данных: Учебное пособие. - СПб.: ГУАП, 2003. - 172 с

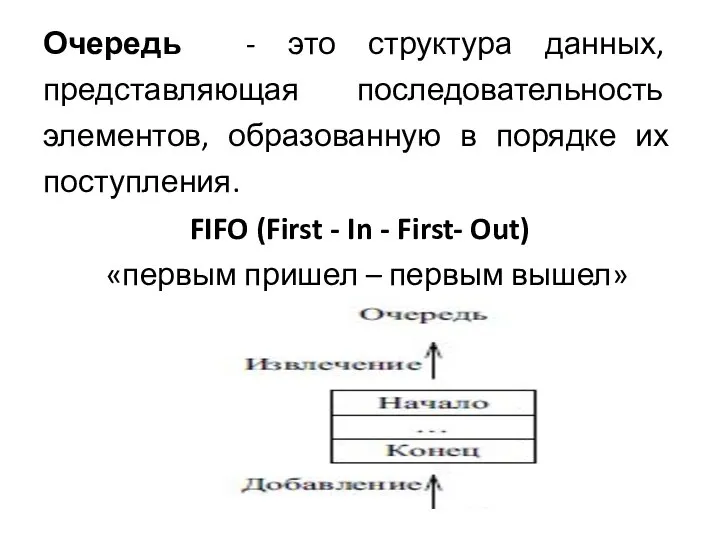
Очередь - это структура данных, представляющая последовательность элементов, образованную в порядке их поступления.
FIFO (First - In - First- Out)
«первым пришел – первым вышел»

Значение очереди в информатике:
1) для моделирования реальных очередей - очереди сообщений, поступающих от терминалов, которые соединены с одним или несколькими центрами связи.
- программы, исследующие поведение сетей для вычисления, например, максимального или среднего времени ожидания, моделируя реакции сети на случайно приходящие сообщения;
моделирование появление посетителей в банке и определение числа окошек, открываемых в различные часы рабочего дня;
очереди захода самолетов на посадку и ожидания разрешения взлета и т.д.

Значение очереди в информатике:
2) решение собственных задач информатики, в частности в области операционных систем ЭВМ. Система имеет дело с целой серией запросов к программным и аппаратным ресурсам: запуск и завершение процессов, доступ к какому-нибудь регистру, устройству или файлу (принтеру, консоли оператора и т. д.). Некоторые типы запросов приоритетны по отношению к другим, но однотипные запросы должны удовлетворяться, вообще говоря, в порядке их поступления.

Очередь - это последовательный список с переменной длиной, в котором включение элементов выполняется только с одной стороны списка (эту сторону часто называют концом или хвостом очереди), а исключение - с другой стороны (называемой началом или головой очереди).

Основные операции над очередью
включение,
исключение,
определение размера,
очистка,
чтение.

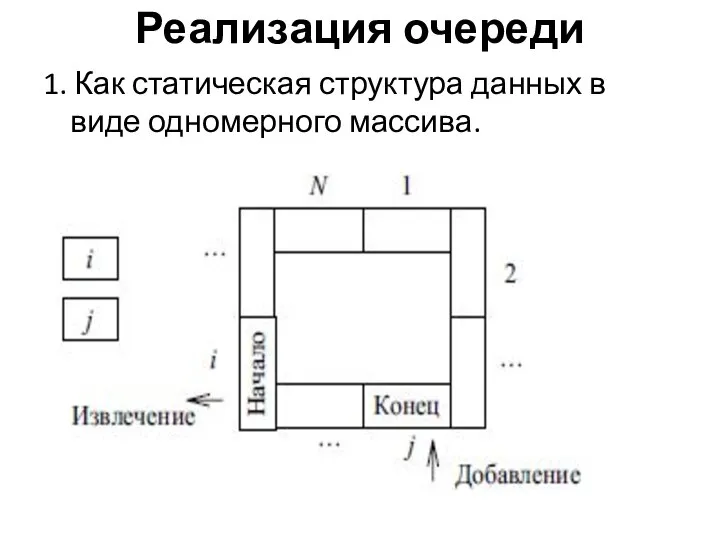
Реализация очереди
1. Как статическая структура данных в виде одномерного массива.

Пример работы c очередью при использовании процедур
maxQ = 5;
R = 0, F = 1
Условие пустоты очереди R < F (0 < 1)

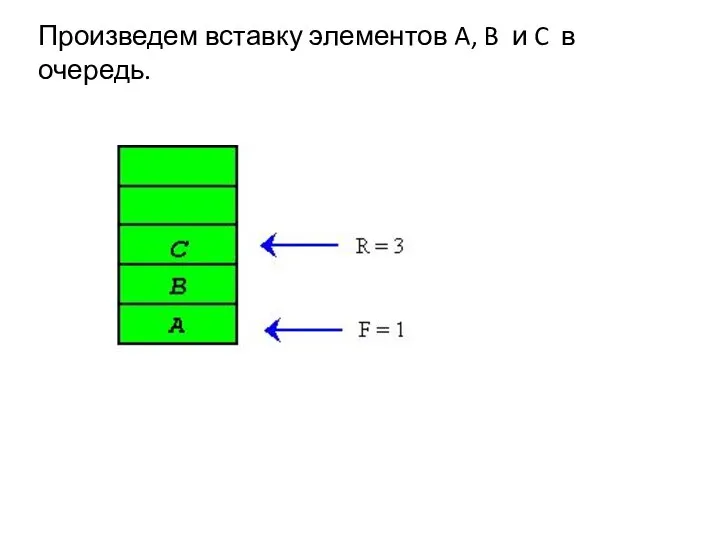
Произведем вставку элементов A, B и C в очередь.

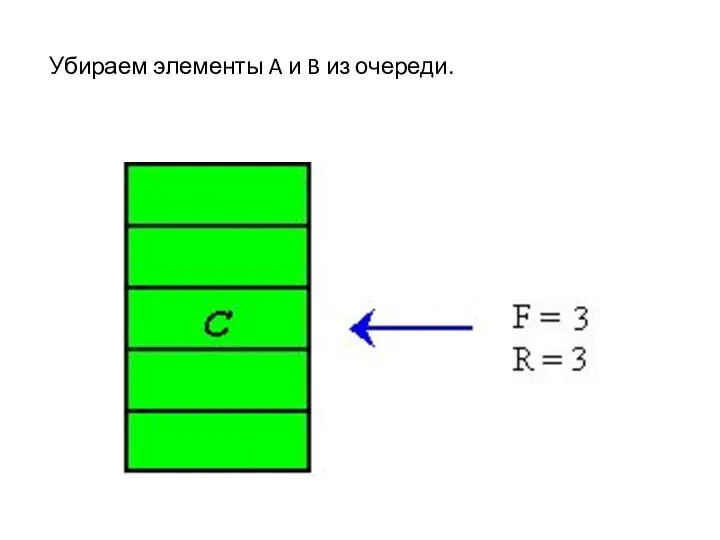
Убираем элементы A и B из очереди.

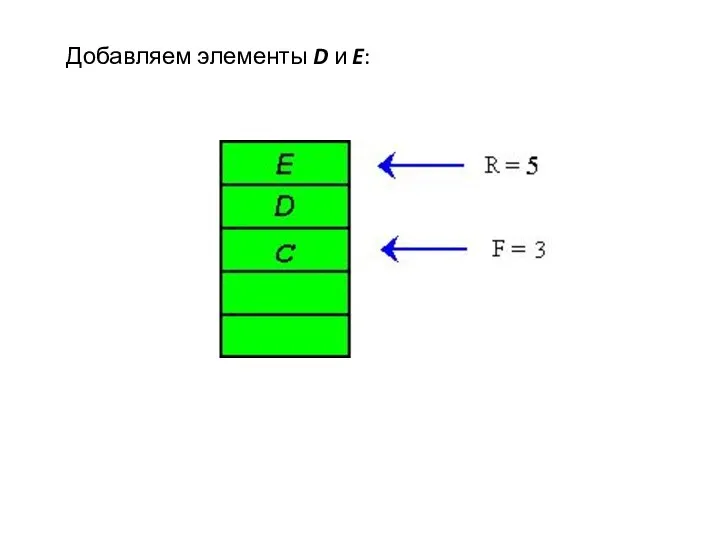
Добавляем элементы D и E:

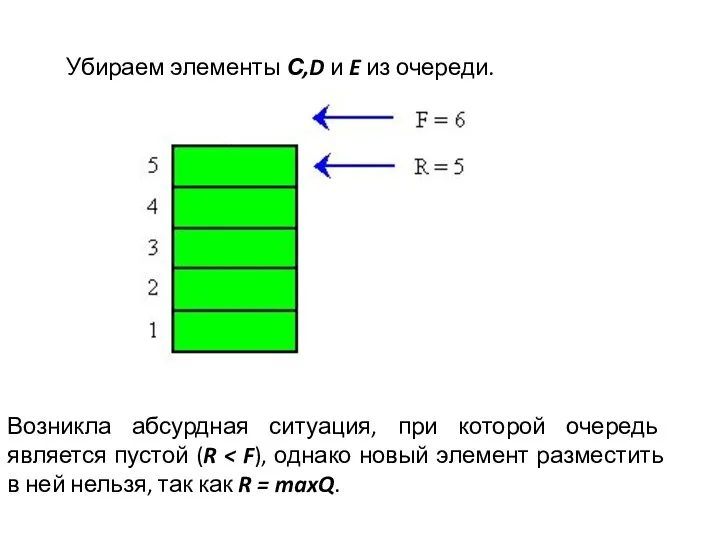
Возникла абсурдная ситуация, при которой очередь является пустой (R < F), однако новый элемент разместить в ней нельзя, так как R = maxQ.
Убираем элементы С,D и E из очереди.

Предотвратить это возможно:
После извлечения очередного элемента из начала очереди осуществить сдвиг всей очереди на один элемент к началу массива. При этом необходимо хранить значение индекса элемента массива, являющегося концом очереди. Переменная F больше не требуется, поскольку первый элемент массива всегда является началом очереди.
Другой способ предполагает рассматривать массив, который содержит очередь в виде замкнутого кольца. Это означает, что даже в том случае, если последний элемент занят, новое значение может быть размещено сразу же за ним на месте первого элемента, если этот первый элемент пуст. При этом необходимо хранить значение индекса элемента массива, являющегося началом очереди, и значение индекса элемента массива, являющегося концом очереди. При добавлении в конец или извлечении из начала очереди, осуществляется смещение значений этих двух индексов по часовой стрелке.

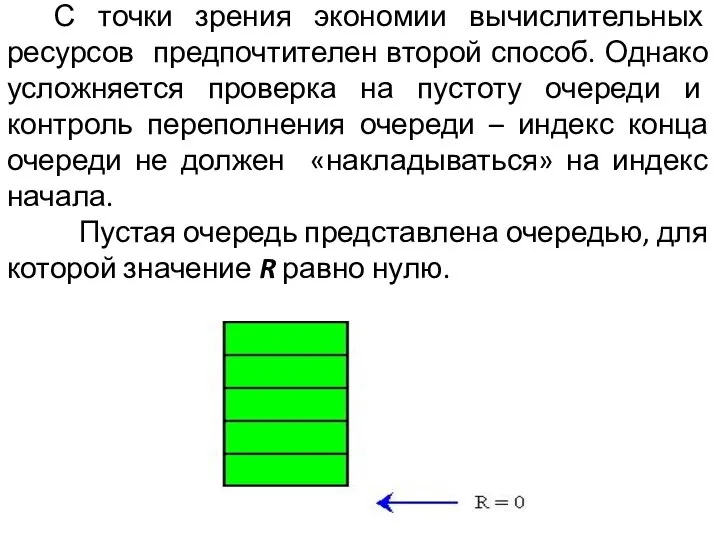
С точки зрения экономии вычислительных ресурсов предпочтителен второй способ. Однако усложняется проверка на пустоту очереди и контроль переполнения очереди – индекс конца очереди не должен «накладываться» на индекс начала.
Пустая очередь представлена очередью, для которой значение R равно нулю.

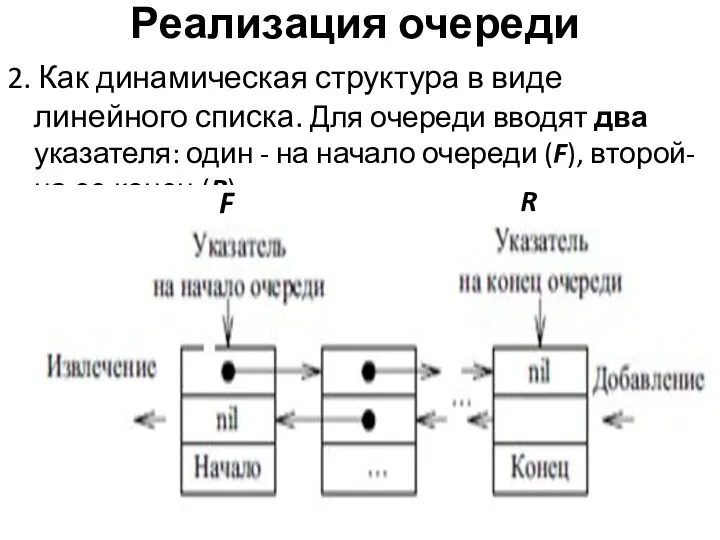
Реализация очереди
2. Как динамическая структура в виде линейного списка. Для очереди вводят два указателя: один - на начало очереди (F), второй- на ее конец (R).
F
R

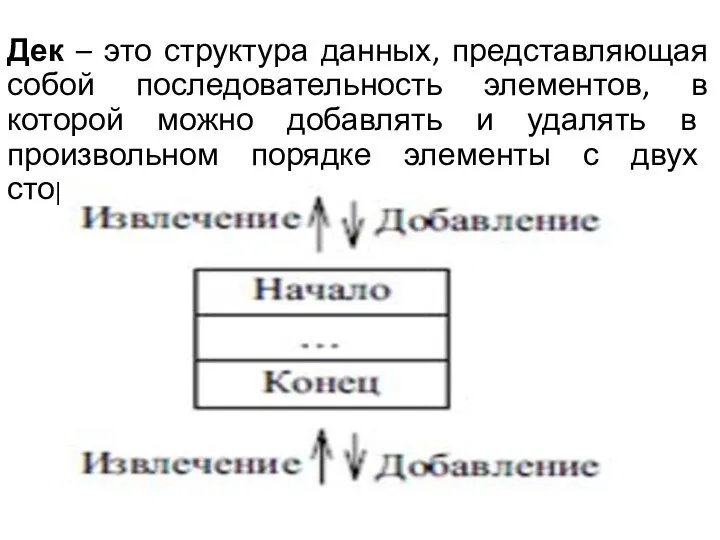
Дек – это структура данных, представляющая собой последовательность элементов, в которой можно добавлять и удалять в произвольном порядке элементы с двух сторон.

Дек - особый вид очереди. Дек (от англ. deq - double ended queue,т.е очередь с двумя концами) - это такой последовательный список, в котором как включение, так и исключение элементов может осуществляться с любого из двух концов списка.
Логическая и физическая структуры дека аналогичны логической и физической структуре кольцевой FIFO-очереди.

Операции над деком:
добавление элемента в начало;
добавление элемента в конец;
извлечение элемента из начала;
извлечение элемента из конца;
определение размера;
проверка пустоты дека;
очистка.

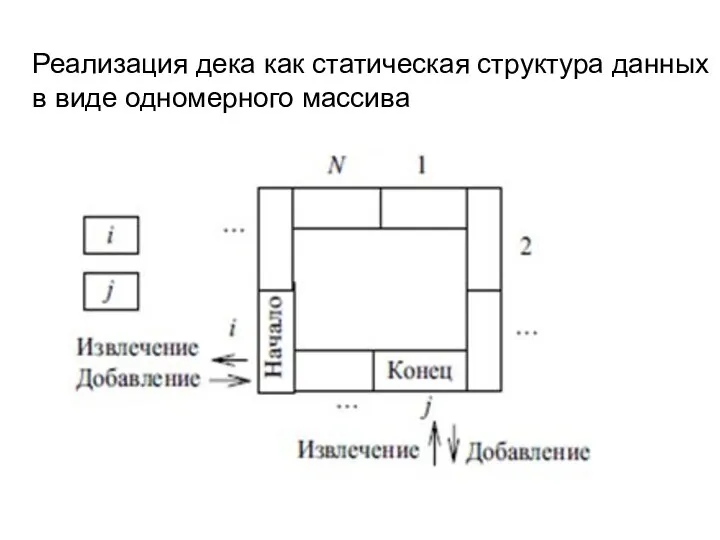
Реализация дека как статическая структура данных в виде одномерного массива

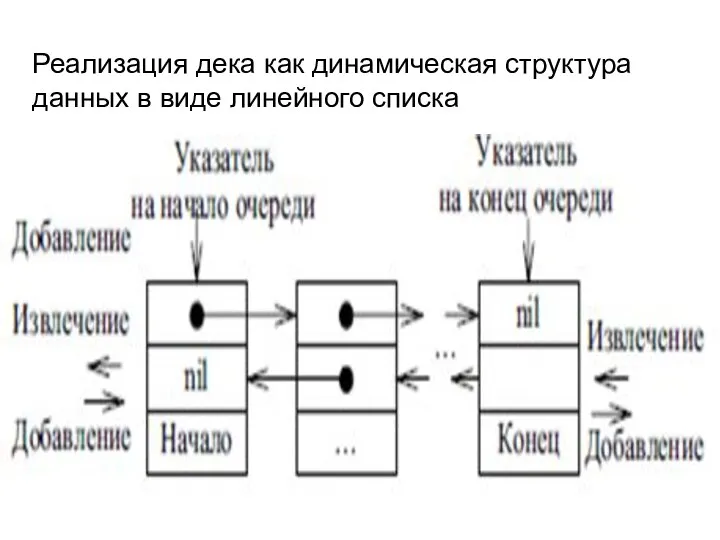
Реализация дека как динамическая структура данных в виде линейного списка