Связь информации с физикой. Концепция информационной (цифровой) физики. Голографический принцип Т'Хофта. Физическая реализация

Цифровая физика — совокупность теоретических взглядов, проистекающих из допущения, что Вселенная по сути описывается информацией и, следовательно, является вычислимой. Из данных предположений следует то, что Вселенная может пониматься как результат работы некоторой компьютерной программы или как некий вид цифрового вычислительного устройства (или, по крайней мере, устройства, математически изоморфного такому устройству).

Машина Тьюринга представляет собой простейшую вычислительную машину с линейной памятью, которая согласно формальным правилам преобразует входные данные с помощью последовательности элементарных действий.
Всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга.

Машиной Зенона называется такая машина Тьюринга, которой требуется 2-n единиц времени для совершения n-го шага. Таким образом, первый шаг требует 0,5 единиц времени, второй — 0,25, третий — 0,125 и так далее, так что за единицу времени совершается бесконечное количество шагов.

Проблема остановки (или проблема останова) — это одна из центральных проблем в теории алгоритмов, которая может неформально быть поставлена в виде:
Даны описание процедуры и её начальные входные данные, требуется определить, завершится ли когда-либо выполнение процедуры с этими данными. Альтернативой этому является то, что она работает всё время без остановки.

Кле́точный автома́т — набор клеток, образующих некоторую периодическую решетку с заданными правилами перехода, определяющими состояние клетки в следующий момент времени через состояние клеток, находящимися от нее на расстоянии не больше некоторого, в текущий момент времени. Как правило, рассматриваются автоматы, где состояние определяется самой клеткой и ближайшими соседями. В качестве решетки обычно рассматривается кубическая решетка. Один из самых интересных примеров клеточного автомата — игра «Жизнь».

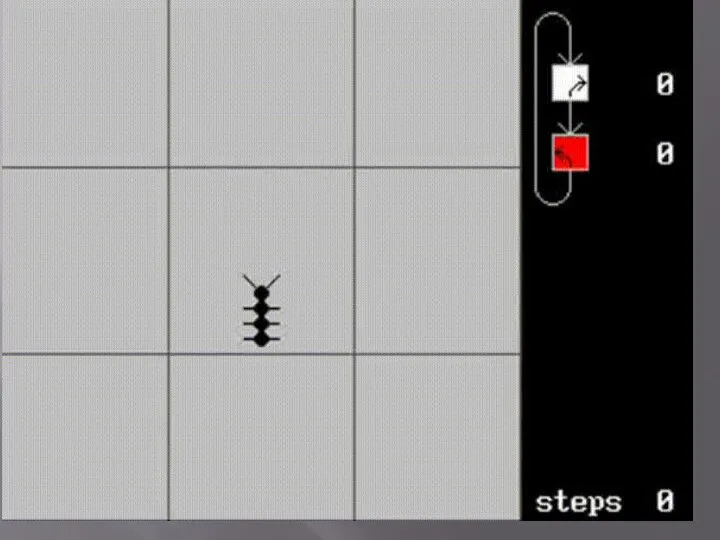
Муравей Лэнгтона — это двумерный клеточный автомат с очень простыми правилами, изобретенный Крисом Лэнгтоном. Муравья можно также считать двумерной машиной Тьюринга с 2 символами и 4 состояниями.
Правила:
Рассмотрим бесконечную плоскость, разбитую на клетки, покрашенные некоторым образом в чёрный и белый цвет. Пусть в одной из клеток находится «муравей», который на каждом шаге может двигаться в одном из четырёх направлений в клетку, соседнюю по стороне. Муравей движется согласно следующим правилам:
На чёрном квадрате — повернуть на 90° влево, изменить цвет квадрата на белый, сделать шаг вперед на следующую клетку.
На белом квадрате — повернуть на 90° вправо, изменить цвет квадрата на чёрный, сделать шаг вперед на следующую клетку.

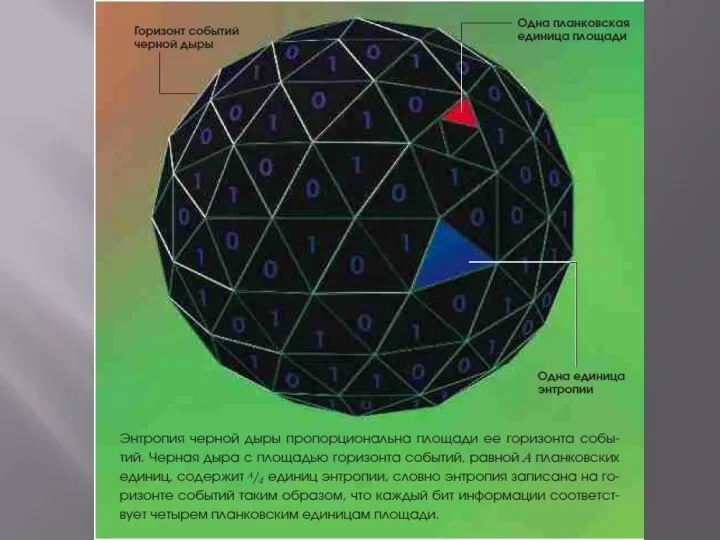
Эпитафия на могиле Больцмана гласит: «S = k log W», и это просто математически изысканный способ сказать, что энтропия объекта пропорциональна числу битов, записанных его микросостоянием. То же самое можно выразить и по-другому: энтропия пропорциональна длине числа возможных микросостояний, если записать его в двоичной системе счисления. В этой формуле k называют постоянной Больцмана.