Тренинг Решение задач ЕГЭ с использованием графов

Немного о графах
Теория графов – раздел дискретной математики, находящий свое приложение в прикладных задачах логистики, проектировании информационных сетей, геоинформационных систем, в химии, информатике и программировании, системотехнике, экономике. Так же графы – мощное средство моделирования.
Родоначальником теории графов считается Леонард Эйлер, но несмотря на историю применения насчитывающую около 3-х веков с момента формулировки им классической задачи о кёнигсберских мостах, понятийный аппарат теории не до конца устоялся1, а сама теория содержит большое количество нерешенных проблем и недоказанных гипотез..
Поляков К.Ю. «Просто графы» Первое сентября. Информатика март 2012

Графы в школе
В школьном курсе графы давно применяются для решения задач в начальной школе «Информатика в играх и задачах» А.В.Горячев.
Коротко теория и применение графов изложено в учебниках профильного курса А.Г.Гейн. А.И.Сенокосов «Информатика и ИКТ» 11 класс.
В качестве дополнительного материала в учебниках И.Г.Семакина 7 класс и учебниках углубленного уровня 10-11 класса. В учебниках Л.Л.Босовой (9 класс).

Графы в ЕГЭ
В настоящее время в ЕГЭ задачи такого типа сводятся к ОДНОЙ задаче: Сколько существует различных путей, ведущих из города А в город Х ...(+ могут быть какие-то дополнительные условия). Хотя рисунки, схемы дорог, могут быть весьма замысловатые.
Обсудим решение с помощью графов:

Задача 1
Диагностическая от 26.01.2015

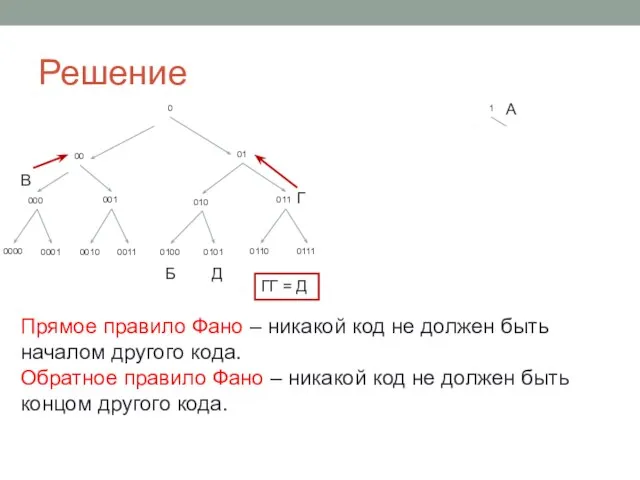
Решение
0
00
01
000
001
010
011
0000
0001
0010
0011
0100
0101
0110
0111
1
10
11
100
101
110
111
1000
1001
1010
1011
1100
1101
1110
1111
А
Б
Д
Г
В
ГГ = Д
Прямое правило Фано – никакой код не должен быть началом другого кода.
Обратное правило Фано – никакой код не должен быть концом другого кода.

Демонстрационный вариант ЕГЭ 2015 г.

Решение

Диагностическая от 26.11.2014 Вариант 1

Решение

Диагностическая от 26.11.2014 вариант 2
9

Задача 5
Диагностическая от 26.01.2015 Вариант 1

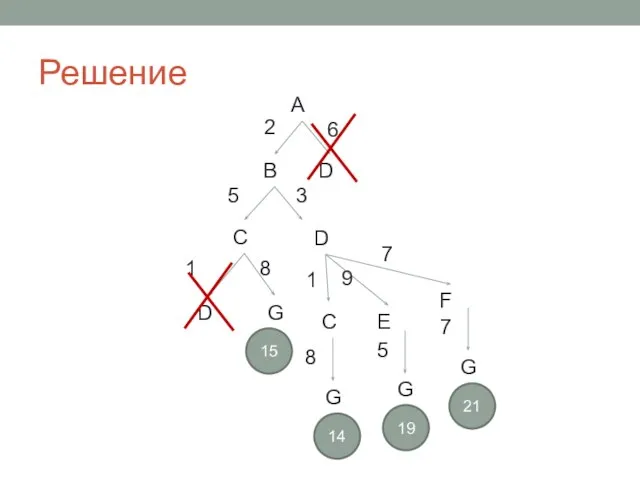
Решение
А
B
D
6
2
C
D
5
3
D
G
1
8
15
C
E
F
1
9
7
14
19
21

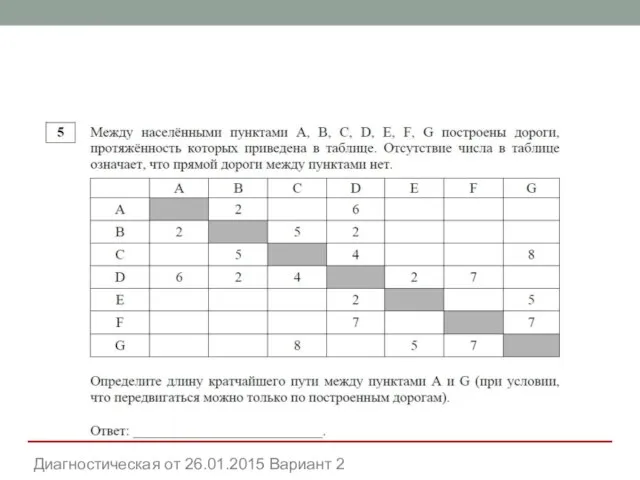
Диагностическая от 26.01.2015 Вариант 2

Решение

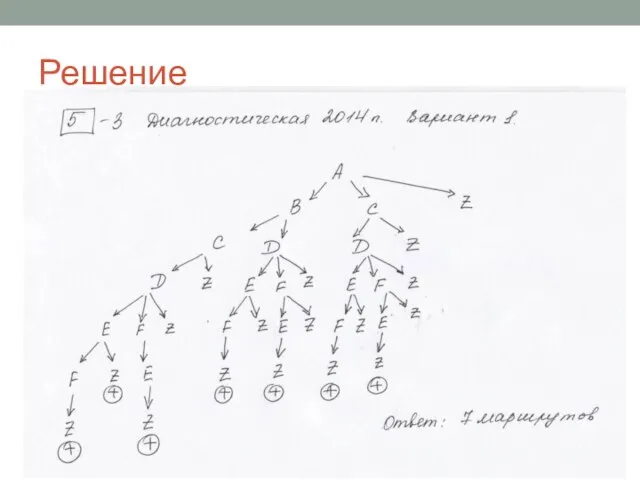
Диагностическая 2014 г. Вариант 1

Решение

Диагностическая 2014 г. Вариант 2
6 маршрутов

Задача 11
Диагностическая от 26.01.2015 Вариант 1

Решение
F(5)
F(4)
F(2)
5
F(3)
F(1)
4
F(1)
F(-1)
2
F(2)
F(0)
3
1
F(0)
F(-2)
F(0)
F(-2)
1
-1
F(1)
F(-1)
2
0
0
-2
0
-2
F(0)
F(-2)
1
-1
0
-2
5+
4+
2+
3+
1+
1
-1+
2+
0+
0
-2+
0
-2+
1
-1+
0
-2
=11

Диагностическая от 26.01.2015 Вариант 2

Решение

Демонстрационный вариант ЕГЭ 2015 г.
49

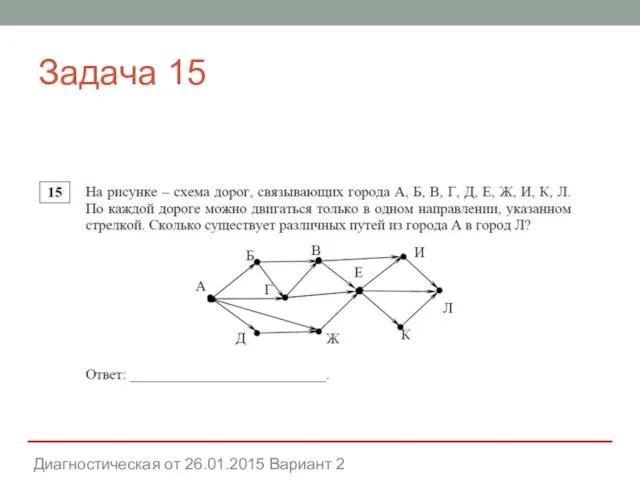
Задача 15
Диагностическая от 26.01.2015 Вариант 2

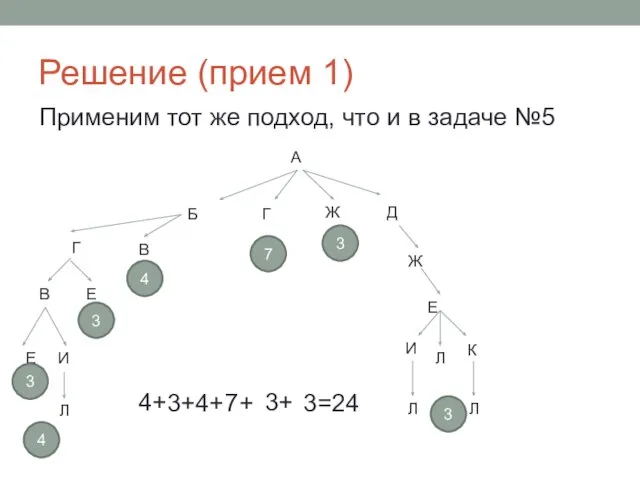
Решение (прием 1)
Применим тот же подход, что и в задаче №5
А
3
3
3
Л
4
3
4
7
4+
3+
4+
7+
3+
3=24

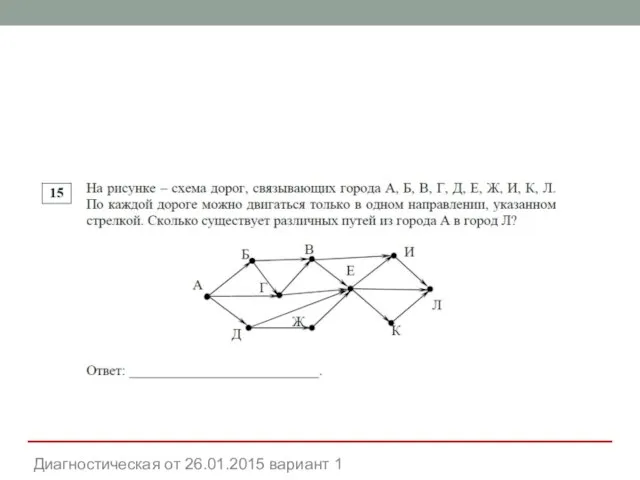
Диагностическая от 26.01.2015 вариант 1

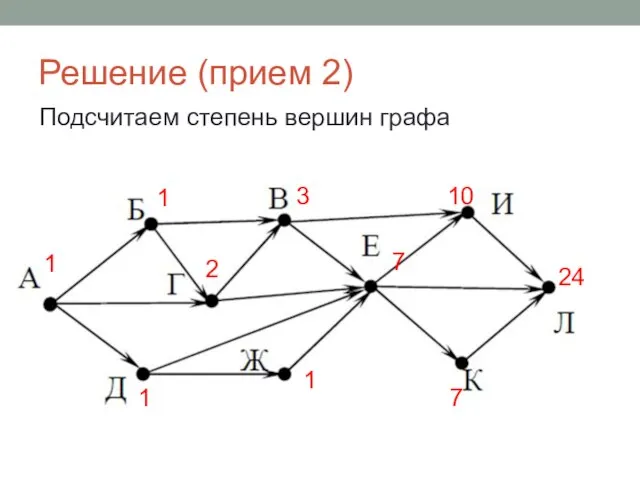
Решение (прием 2)
Подсчитаем степень вершин графа
1
1
2
1
3
1
7
10
7
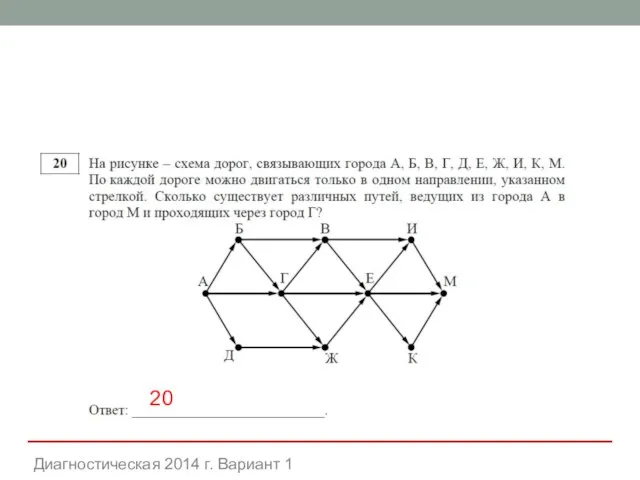
24

Диагностическая 2014 г. Вариант 1
20

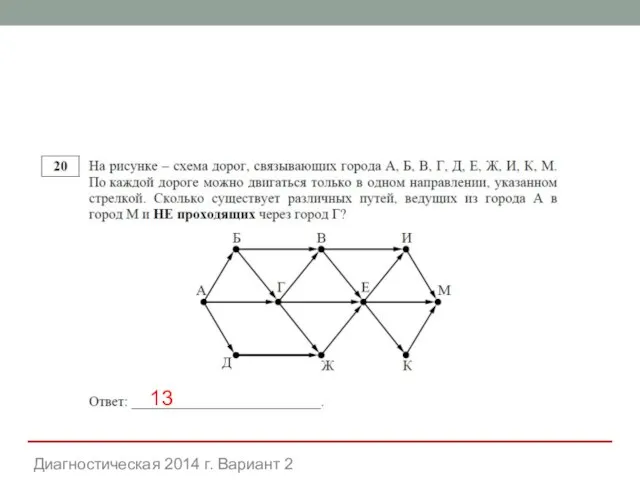
Диагностическая 2014 г. Вариант 2
13

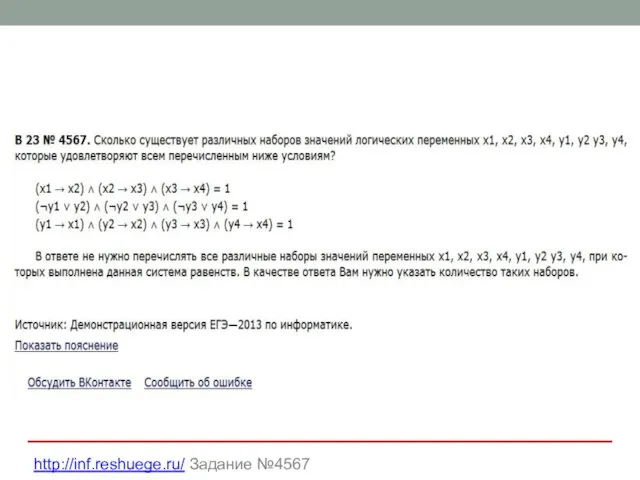
Задача 23
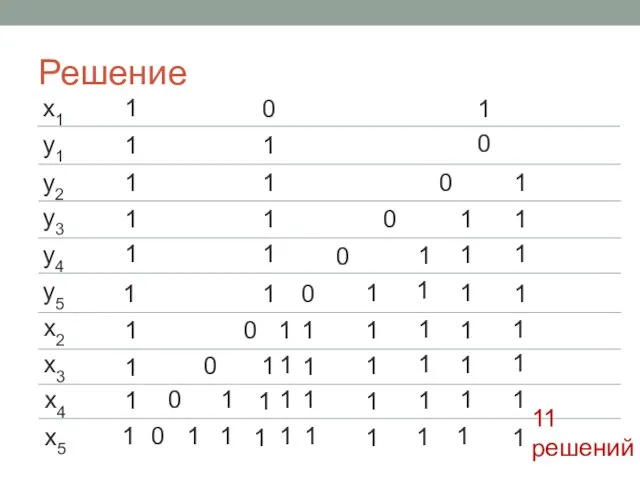
https://ege.yandex.ru/informatics/ Вариант 1

Решение
x1
y1
y2
y3
y4
y5
x2
x3
x4
x5
1
1
0
1
1
0
1
1
1
0
1
1
0
1
1
1
1
0
1
1
1
1
1
0
1
1
1
1
1
1
0
1
1
1
1
1
1
0
1
1
1
1
1
1
1
1
0
1
1
1
1
1
1
1
1
1
0
1
1
1
1
1
1
1
1
1
11 решений

http://inf.reshuege.ru/ Задание №4567

Решение

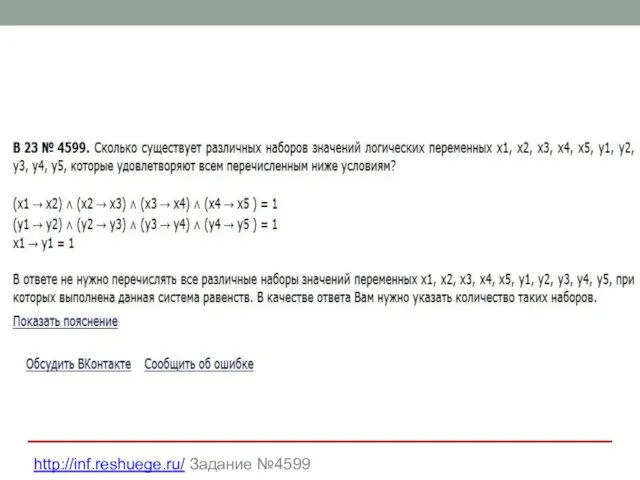
http://inf.reshuege.ru/ Задание №4599

Решение

Демонстрационный вариант ЕГЭ 2014 г.

Решение

Задача 26
Демонстрационный вариант ЕГЭ 2015

Решение
Задачу проверяет эксперт. Поэтому ВАЖНО правильно ее оформить
1. Коротко записываем условие, к нему будем обращаться в ходе решения задачи.
+1
+3 ! >=35
*2
Задание 1 а) S=18… 34 Во всех этих случаях Петя должен удвоить кучу камней и выиграть. При значениях <18 невозможно одним ходом (+1;+3;*2) получить победное число камней

Задание 1 б)
При S=17 как бы ни пошел Петя (17+1=18; 17+3=20; 17*2=34) Ваня удвоит количество камней в куче и выиграет (18*2=36; 20*2=40; 34*2=68).

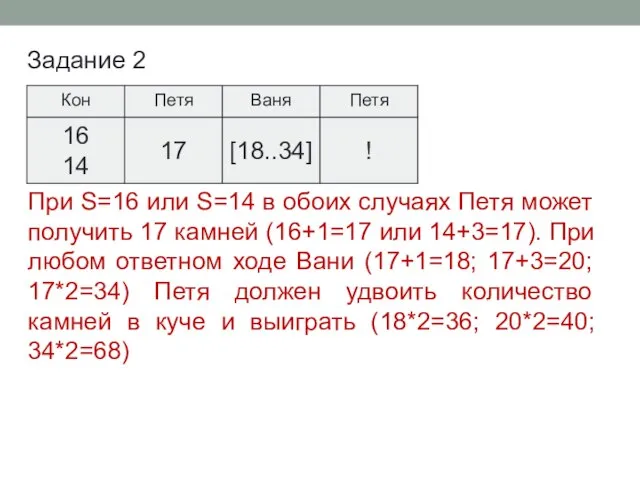
Задание 2
При S=16 или S=14 в обоих случаях Петя может получить 17 камней (16+1=17 или 14+3=17). При любом ответном ходе Вани (17+1=18; 17+3=20; 17*2=34) Петя должен удвоить количество камней в куче и выиграть (18*2=36; 20*2=40; 34*2=68)

Задание 3
16
14
17
[18…34]
!
8
13
15
11
9
26
!
30

При S=15
В этом дереве в каждой позиции, где должен ходить Петя разобраны все возможные ходы, а для позиции, где должен ходить Ваня приведены только ходы, соответствующие выбранной выигрышной стратегии

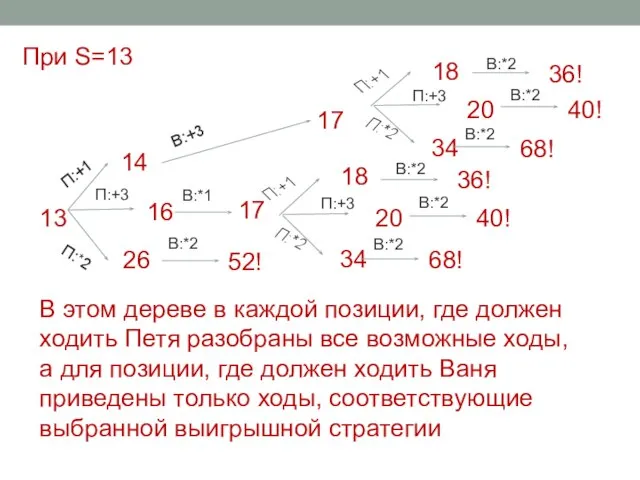
При S=13
В этом дереве в каждой позиции, где должен ходить Петя разобраны все возможные ходы, а для позиции, где должен ходить Ваня приведены только ходы, соответствующие выбранной выигрышной стратегии

Диагностическая от 26.11.2014 Вариант ИН103001

Решение