Уровни моделирования

ОСОБЕННОСТИ МОДЕЛИРОВАНИЯ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ СВАРКИ
Выделим три особенности процессов при сварке как объектов расчета:
Неоднородность среды
Нелинейность явлений
Системность процесса сварки
Физико-химические процессы, протекающие при сварке:
Тепловые
Металлургические
Деформационные
Диффузионные
…

ТИПОВЫЕ ЗАДАЧИ МОДЕЛИРОВАНИЯ ТЕХНОЛОГИИ СВАРКИ
Расчет режимов сварки по геометрическим критериям размеров швов.
Оценка формирования шва по критериям допустимых уравнений дефектов формы и сплошности шва.
Оценка свариваемости высокопрочных сталей и других конструкционных материалов по критериям отсутствия трещин, обеспечения соответствующего структурного состояния и физико-механических свойств.
Оценка несущей способности сварных конструкций и соединений.
...

РАСЧЕТНЫЕ ПРОЦЕДУРЫ
Анализ – определение свойств объекта по его описанию. Виды:
– Одновариантный – при заданном наборе входных и внутренних параметров определяются выходные параметры.
– Многовариантный – внешние и внутренние параметры варьируются в некоторой области.
Синтез – создание объекта с заданными свойствами. Виды:
– Структурный – определение структуры объектов, то есть составляющих элементов и способов их связи между собой.
– Параметрический – определение числовых значений параметров при заданной структуре.
Оптимизация – определение наилучших в смысле производительности, стоимости, качества и других значений параметров.
Задачи синтеза и оптимизации полностью включают в себя задачи анализа

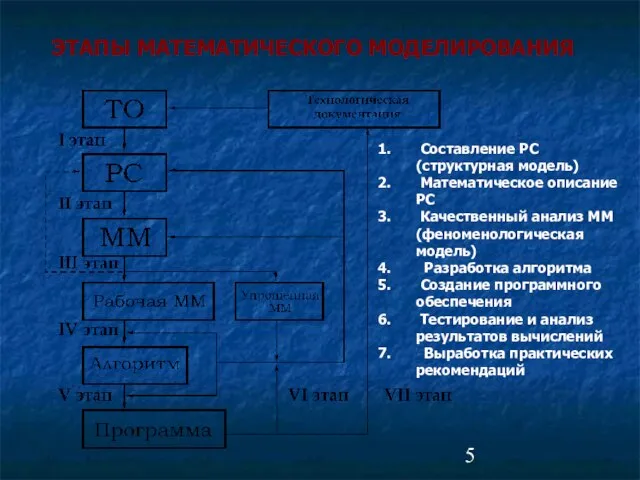
ЭТАПЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
Составление РС (структурная модель)
Математическое описание РС
Качественный анализ ММ (феноменологическая модель)
Разработка алгоритма
Создание программного обеспечения
Тестирование и анализ результатов вычислений
Выработка практических рекомендаций

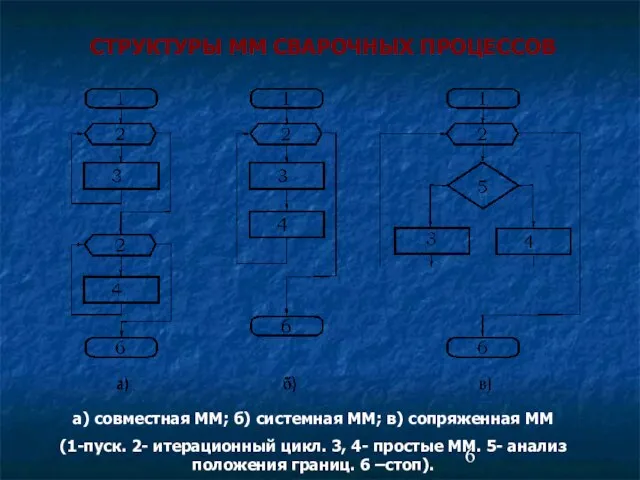
СТРУКТУРЫ ММ СВАРОЧНЫХ ПРОЦЕССОВ
а) совместная ММ; б) системная ММ; в) сопряженная ММ
(1-пуск. 2- итерационный цикл. 3, 4- простые ММ. 5- анализ положения границ. 6 –стоп).

СВОЙСТВА МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
Полнота ММ позволяет отразить в достаточной мере именно те характеристики и особенности ТО, которые интересуют нас с точки зрения поставленной цели
Точность ММ дает возможность обеспечить приемлемое совпадение реальных и найденных при помощи ММ значений выходных параметров ТО.
Адекватность ММ — это способность ММ отражать характеристики ТО с относительной погрешностью не более некоторого заданного значения δ
Экономичность ММ оценивают затратами на вычислительные ресурсы (машинное время и память), необходимые для реализации ММ на ЭВМ.
Робастность ММ (от английского слова robust — крепкий, устойчивый) характеризует ее устойчивость по отношению к погрешностям исходных данных.
Наглядность ММ является ее желательным, но необязательным свойством.

И наконец, исходя их определения ММ, вытекает свойство универсальности ММ. Это можно объяснить тем, что в математике используют абстрактные основополагающие понятия, немногочисленные, но весьма емкие по содержанию.
Это позволяет конкретные факты из самых различных областей знаний рассматривать как проявление этих понятий и отношений между ними. Совокупность таких понятий и отношений, выраженных при помощи системы математических символов и обозначений и отражающих некоторые свойства изучаемого объекта, и называют математической моделью этого объекта.
В данном случае математика выступает, по существу, в роли универсального языка науки. Его универсальность французский математик Анри Пуанкаре (1854-1912) определил всего одной фразой: „Математика — это искусство называть разные вещи одним и тем же именем".
СВОЙСТВА МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

1. МОДЕЛИРОВАНИЕ ПАРАМЕТРОВ ТЕРМИЧЕСКОГО ЦИКЛА ЗТВ
для массивного тела (трехмерного теплоотвода):
(1)
для пластины (двухмерного теплоотвода):
(2)
ТИПИЧНЫЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОЦЕССОВ СВАРКИ
Основными параметрами термического цикла ЗТВ при однопроходной сварке или наплавке являются максимальная тем-ра Тм , мгновенная скорость охлаждения ω при данной тем-ре Т и длительности нагрева tH выше Т.
В зависимости от схемы распространения теплоты применяют различные формулы для расчета скорости охлаждения:

критическую толщину листа δк можно определить, из (1) и (2):
(3) Учитывая то, что ω постоянно уменьшается по мере снижения Т, понятие скорости охлаждения в интервале температур теряет смысл. Предпринята попытка ввести эквивалентную (постоянную) скорость охлаждения WЭ в интервале температур, достаточно хорошо отражающую динамику охлаждения металла шва:
(4)
где S – величина температурно-временной области, ограниченной участком кривой термического цикла сварки в интервале Т1 – Т2.
МОДЕЛИРОВАНИЕ ПАРАМЕТРОВ ТЕРМИЧЕСКОГО ЦИКЛА ЗТВ

МОДЕЛИРОВАНИЕ ПАРАМЕТРОВ ТЕРМИЧЕСКОГО ЦИКЛА ЗТВ
Для характеристики охлаждения зоны термического влияния в диапазоне температур вместо средней скорости охлаждения наиболее целесообразно использовать обратную ей величину – время охлаждения или длительность пребывания различных точек зоны термического влияния в интервале температур. Установлено, что для всех точек зоны шва, нагретых выше 900°С, время охлаждения в интервале 800-500 °С приблизительно равно.
Диапазон температур 800°- 500°С является одним из важнейших и определяет кинетику фазового превращения в стали. В настоящее время охлаждение в интервале 800°- 500°С , обозначаемое t8/5,
признано основным критерием, определяющим механические свойства сварных соединений низколегированных сталей. В ряде стран, например в ФРГ, время t8/5 вводится в нормативные документы по сварке низколегированных сталей.

МОДЕЛИРОВАНИЕ ПАРАМЕТРОВ ТЕРМИЧЕСКОГО ЦИКЛА ЗТВ
для массивного тела (трехмерного теплоотвода):
(5)
для пластины (двухмерного теплоотвода):
(6)
критическая толщина листа δк:
(7)
Формулы для расчета величины t8/5 :

В уравнениях (5) – (7) напряжение дуги U изменяется в вольтах, сила тока I – в амперах, скорость сварки v – сантиметрах в секунду, температура подогрева Т0 - в градусах Цельсия.
Кроме того, необходимо ввести коэффициенты термического КПД нагрева η в зависимости от способа дуговой сварки и коэффициенты двухмерного (F2) или трехмерного (F3) теплоотвода, а также учесть зависимость теплофизических констант от температуры для практически используемого диапазона рабочих температур 20°-250°С.
МОДЕЛИРОВАНИЕ ПАРАМЕТРОВ ТЕРМИЧЕСКОГО ЦИКЛА ЗТВ

для массивного тела (трехмерного теплоотвода):
(8)
для пластины (двухмерного теплоотвода):
(9)
критическая толщина листа δк:
(10)
МОДЕЛИРОВАНИЕ ПАРАМЕТРОВ ТЕРМИЧЕСКОГО ЦИКЛА ЗТВ
В итоге :
Выражения ( ) и ( ) учитывают теплофизические константы низколегированных сталей и их зависимость от температуры в интервале 20°- 250°С.

МОДЕЛИРОВАНИЕ ПАРАМЕТРОВ ТЕРМИЧЕСКОГО ЦИКЛА ЗТВ
Табл. 1 - Значения термического КПД нагрева.

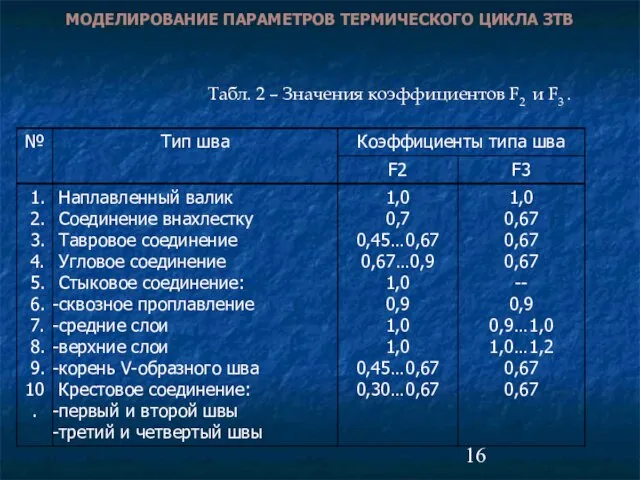
МОДЕЛИРОВАНИЕ ПАРАМЕТРОВ ТЕРМИЧЕСКОГО ЦИКЛА ЗТВ
Табл. 2 – Значения коэффициентов F2 и F3 .

Математическая модель плавления электродной проволоки должна устанавливать детерминированные взаимосвязи между характеристиками плавления металла электродной проволоки:
αр — коэффициент расплавления,
vэ — линейная скорость плавления электродной проволоки;
и его физическими свойствами:
(γ, — плотность металла;
Тпл — температура плавления;
Ткип — температура кипения;
с — удельная теплоемкость;
ΔНпл — скрытая теплота плавления;
ρ — удельное электросопротивление;
φв — работа выхода электрона;
а также параметрами режима сварки: (Iсв, Uд, dэ, lв).
2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПЛАВЛЕНИЯ ЭЛЕКТРОДНОЙ ПРОВОЛОКИ ПРИ ДУГОВОЙ СВАРКЕ

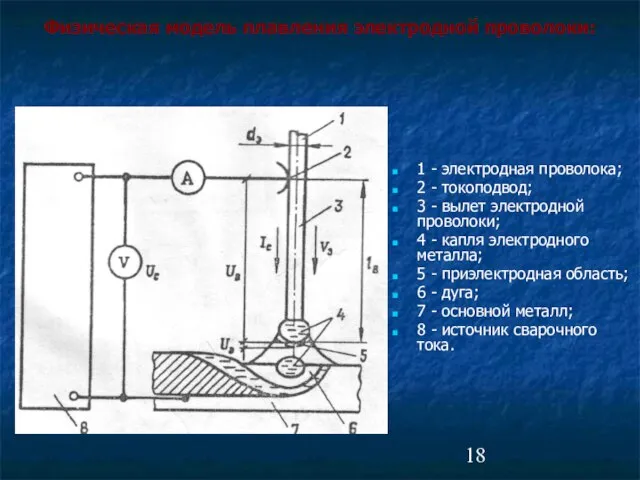
1 - электродная проволока;
2 - токоподвод;
3 - вылет электродной проволоки;
4 - капля электродного металла;
5 - приэлектродная область;
6 - дуга;
7 - основной металл;
8 - источник сварочного тока.
Физическая модель плавления электродной проволоки:

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПЛАВЛЕНИЯ ЭЛЕКТРОДНОЙ ПРОВОЛОКИ ПРИ ДУГОВОЙ СВАРКЕ
Математическая модель плавления электрода основана на уравнении баланса энергии на электроде:
Wпл=Wэ + Wв, (1)
где Wпл — расход энергии на нагрев и плавление электродной проволоки; Wэ и Wв, — приход энергии на торце электрода и на вылете электродной проволоки.
Выразив расход энергии через массу расплавленной электродной проволоки Мэ (Мэ = FэLэγтв) и теплосодержание капель электродного металла Нкап, получаем выражения для определения коэффициента расплавления αр и линейной скорости плавления электрода vэ:
(2)
(3)

Падение напряжения электрода Uэ = Uа + φв , (4)
где Uа – падение напряжения на аноде. Uа мало зависит от материала анода и состава газовой фазы и может быть принято Uа=(2,43±0,29) В.
Падение напряжения на вылете определяется при постоянном удельном сопротивлении ρср для диапазона температур на вылете от То до Тпл :
(5)
Теплосодержание капель электродного металла определяем при условии, что Ткап = 0,9Ткип:
Нкап = сср(Тпл-Т0) + ΔНпл + сж(Ткап - Тпл), (6)
где