ВКР: Применение методов оптимизации для формирования обобщенных кодов Баркера

Актуальность задачи
Актуальность предлагаемого исследования обусловлена широким использованием последовательностей Баркера в радиолокации, цифровой речи, ультразвуковом сканировании, GPS, Wi-Fi.
Коды Баркера длиной N, равной 11 и 13, используются в радиолокационных системах с расширенным спектром прямой последовательности.

Цель работы
Целью работы является разработка алгоритмов и программ, реализующих методы оптимизации, применимых к задаче об обобщении кодов Баркера.

Последовательности Баркера
Последовательность Баркера – это числовая последовательность x1, x2, … , xN, где каждый элемент равен 1 или -1, причем
где
для 1 – N ≤ k ≤ N – 1, кроме 0.

Известные последовательности Баркера
С точностью до реверсирования
порядка и смены знаков каждого
из элементов на данный момент
известно только 9 кодов Баркера.

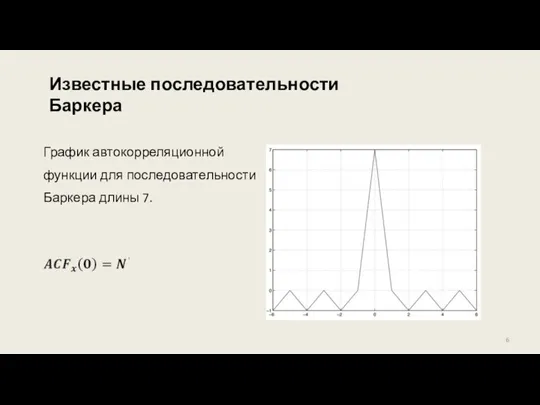
График автокорреляционной
функции для последовательности
Баркера длины 7.
- “peak”
Известные последовательности Баркера

Постановка основной задачи
Требуется найти вектор х, при котором функция F(x) принимает наименьшее возможное значение среди всех тех значений, которые она принимает для допустимых х:

Алгоритм:
При решении были использованы метод полного перебора и метод покоординатного спуска – замена xk на –xk.
При росте N время, затраченное на поиск нужной последовательности методом полного перебора, становится большим.
Поэтому перейдем к алгоритму методу покоординатного спуска.
Решение основной задачи

Решение основной задачи
Суть метода поокординатного спуска заключается в том, чтобы заменять
координату xk на –xk и идти в сторону уменьшения критерия качества. Если
критерий качества уменьшился, то координату –xk оставляем и переходим к
xk-1, иначе возвращаем начальное значение xk и переходим к xk-1.

Решение основной задачи
Вычисления:
N = 7:
Для начальной точки х = (1, 1, 1, 1, 1, 1, 1) получилась
тупиковая точка ẋ = (1, 1, 1, -1, -1, 1, -1), минимум F(ẋ) = 1
Точка ẋ также является кодом Баркера
N = 11:
Для начальной точки х = (1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1) получилась
тупиковая точка ẋ = (1, 1, 1, -1, 1, 1, 1, -1, -1, 1, -1), минимум F(ẋ) = 3
N = 19:
Для начальной точки х = (1, 1, 1, … , 1, -1, -1) получилась
тупиковая точка ẋ = (1, 1, 1, 1, -1, 1, 1, -1, 1, -1, -1, 1, 1, 1, -1, -1, 1, -1, -1),
минимум F(ẋ) = 3

Преимущество направленного перебора перед полным – при программной реализации алгоритма смогли избежать полного перебора всех функций.
Не все тупиковые точки являются оптимальными.
Минимум функции F(x) сильно зависит от выбора начальной точки.
Полученные тупиковые точки можно использовать как начальные
приближения в более серьезных методах оптимизации.
Перейдем к эквивалентной задаче, которая имеет стандартный вид и гладкий
критерий качества.
Вывод

Постановка эквивалентной задачи

Имеется задача
При ограничениях
Тогда целесообразно использовать штрафную функцию такого вида:
Далее переходим от исходной задачи к задаче безусловной минимизации:
Описание метода штрафных функций

Алгоритм метода штрафных функций
Начальные данные
Выбираем eps > 0, начальную точку x0 и параметр штрафа.
Первый шаг
Решаем задачу
Полагаем, что новый х равен оптимальному решению задачи и переходим к следующему шагу.
Второй шаг
Если , то останавливаемся.
В противном случае увеличиваем k и переходим к первому шагу.

Алгоритм нахождения вектора для основной задачи :
Взять несколько тупиковых точек, которые были получены при решении основной задачи.
Взять эти точки в качестве начальных для метода штрафных функций.
Составить штрафную функцию и минимизировать ее.
Округлить полученные значения компонент вектора до 1 или -1.
Продолжить применение метода штрафных функций с полученной точкой в качестве начальной, если результат не улучшился – значит, получен квазиоптимум.
Решение эквивалентной задачи

Решение эквивалентной задачи
Вычисления:
N = 11
Начальный вектор: 1, 1, 1, -1, 1, -1, -1, 1, -1, -1, -1
Минимум = 3
Итоговый вектор: 1, 1, 1, -1, 1, -1, -1, 1, -1, -1, -1
Минимум = 3
N = 19
Начальный вектор: 1, 1, 1, 1, -1, 1, 1, -1, 1, -1, -1, 1, 1, 1, -1, -1, 1, -1, -1
Минимум = 4
Итоговый вектор: -1, 1, 1, 1, 1, 1, 1, -1, 1, -1, -1, 1, 1, -1, -1, -1, 1, 1, -1
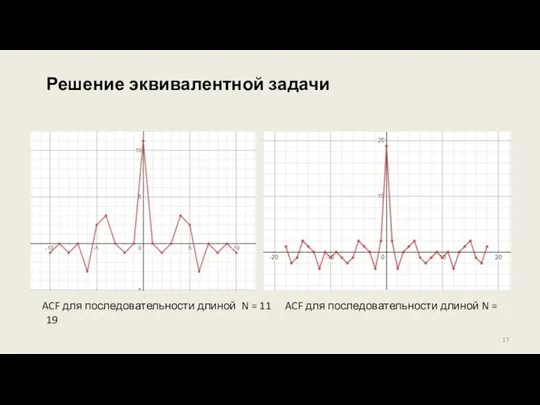
Минимум = 3

Решение эквивалентной задачи
ACF для последовательности длиной N = 11 ACF для последовательности длиной N = 19

Решение эквивалентной задачи
N = 30
Начальный вектор: 1, 1, 1, 1, 1, 1, -1, 1, 1, -1, -1, 1, 1, 1, 1, -1, -1, -1, 1, -1, 1, -1,
-1, 1, 1, 1, -1, -1, 1, -1. Минимум = 6
Итоговый вектор: 1, 1, 1, 1, 1, 1, -1, -1, 1, -1, -1, -1, 1, -1, 1, -1, -1, -1, 1, 1, 1, -1,
-1, 1, -1, 1, -1, -1, 1, -1. Минимум = 4
N = 40
Начальный вектор: 1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, -1, 1, -1, 1, 1, -1, -1, 1, -1, -1, 1, 1, 1, 1,
-1, -1, -1, 1, -1, 1, -1, -1, 1, 1, 1, -1, -1, 1, -1. Минимум = 6
Итоговый вектор: 1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, -1, 1, -1, 1, 1, -1, -1, 1, -1, -1, 1, 1, 1, 1, -1,
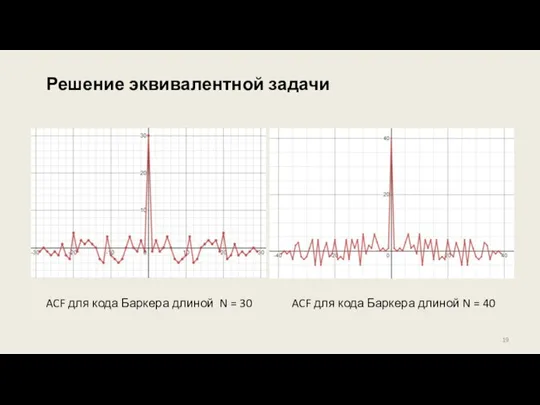
-1, -1, 1, -1, 1, -1, -1, 1, 1, 1, -1, -1, 1, -1. Минимум = 6

Решение эквивалентной задачи
ACF для кода Баркера длиной N = 30 ACF для кода Баркера длиной N = 40

Решение эквивалентной задачи
N = 45
Начальный вектор: 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, -1, 1, -1, 1, -1, 1, 1, -1, -1, 1, -1,
-1, 1, 1, 1, 1, -1, -1, -1, 1, -1, 1, -1, -1, 1, 1, 1, -1, -1, 1, -1. Минимум = 6
Итоговый вектор: 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, -1, 1, -1, 1, -1, 1, 1, -1, -1, 1, -1, -1,
1, 1, 1, 1, -1, -1, -1, 1, -1, 1, -1, -1, 1, 1, 1, -1, -1, 1, -1. Минимум = 6
N = 50
Начальный вектор: 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, -1, 1, -1, -1, 1, -1, 1, -1, 1, 1,
-1, -1, 1, -1, -1, 1, 1, 1, 1, -1, -1, -1, 1, -1, 1, -1, -1, 1, 1, -1, -1, -1, 1, -1. Минимум = 8
Итоговый вектор: 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, -1, 1, -1, -1, -1, 1, -1, 1, 1, -1, 1, -1, 1, -1, 1, 1,
-1, -1, 1, -1, 1, 1, 1, -1, -1, -1, -1, -1, 1, 1, 1, -1, -1, 1, 1, -1, -1, -1, 1, 1. Минимум = 6

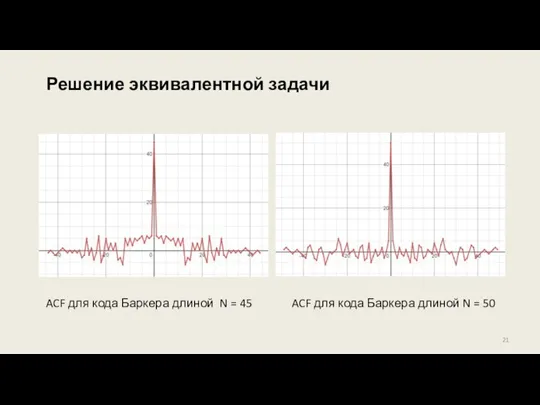
Решение эквивалентной задачи
ACF для кода Баркера длиной N = 45 ACF для кода Баркера длиной N = 50

Выводы
Применены современные методы оптимизации к эквивалентной задаче.
Рассмотрены случаи для N > 19.
Для случая N = 11 критерий качества не был улучшен.
Для N = 19, 30, 50, 60 применение метода штрафных функций позволило улучшить критерий качества и приблизиться к минимуму, но все же его не достигнуть.
Для N = 40, 45 критерий качества либо не менялся, либо только ухудшался.