Содержание
- 2. 2 Термин программирование в названии означает «обоснованную и заранее заданную (запрограммированную) последовательность оптимизирующих действий». Прямого отношения
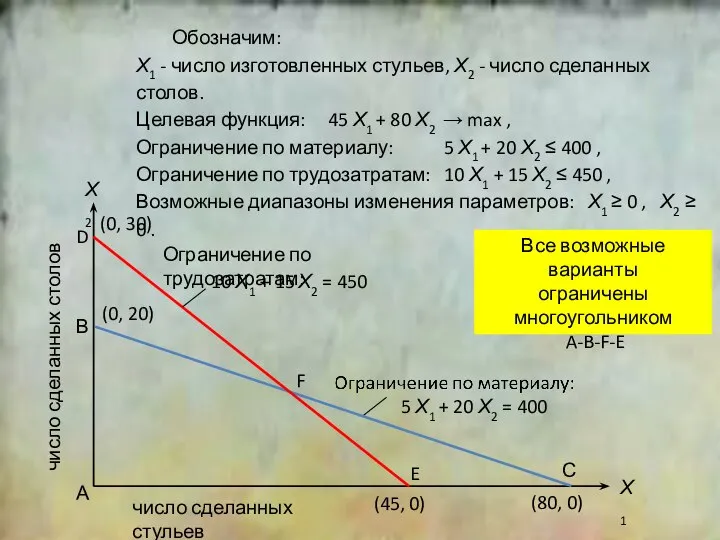
- 3. 2 Обозначим: Х1 - число изготовленных стульев, Х2 - число сделанных столов. Целевая функция: 45 Х1
- 4. 2 Х1 Х2 число сделанных стульев число сделанных столов (0, 30) Ограничение по трудозатратам: 10 Х1
- 5. 2 Х1 Х2 число сделанных стульев число сделанных столов (0, 30) Ограничение по трудозатратам: 10 Х1
- 6. 2 Х1 Х2 число сделанных стульев число сделанных столов (0, 30) Ограничение по трудозатратам: 10 Х1
- 8. Скачать презентацию




 Продвинутые основы Блюпринтов. Лекция 6
Продвинутые основы Блюпринтов. Лекция 6 Добавление таблиц
Добавление таблиц Открывать, редактировать и сохранять файлы в прикладных программах. Критерии оценивания
Открывать, редактировать и сохранять файлы в прикладных программах. Критерии оценивания МедиаThor в VK
МедиаThor в VK Презентация на тему Язык гипертекстовой разметки - html
Презентация на тему Язык гипертекстовой разметки - html  Решение задач нелинейного программирования (ЗНЛп) в пакете Excel
Решение задач нелинейного программирования (ЗНЛп) в пакете Excel урок 3
урок 3 Composition & Unit testing with MS test
Composition & Unit testing with MS test Имитация объема в photoshop
Имитация объема в photoshop I am a Screen Leader
I am a Screen Leader Прямое и стилевое форматирование текста. Обработка текстовой информации
Прямое и стилевое форматирование текста. Обработка текстовой информации Электронное согласование договора
Электронное согласование договора Программы. Мосты
Программы. Мосты 6-12-1-grafiki-i-diagrammy
6-12-1-grafiki-i-diagrammy Создание графических изображений
Создание графических изображений Изучение возможностей и синтаксиса Python: Ветвление и исключения. 3 занятие
Изучение возможностей и синтаксиса Python: Ветвление и исключения. 3 занятие Компьютерные сети как средства массовой коммуникации
Компьютерные сети как средства массовой коммуникации Электронные брошюры Навигатор для абитуриентов
Электронные брошюры Навигатор для абитуриентов Строки в C#
Строки в C# Операционные Системы
Операционные Системы Обработка массивов и матриц
Обработка массивов и матриц Телеканал Гейм Шоу
Телеканал Гейм Шоу Функция fmod (x,y)
Функция fmod (x,y) Методы математического описания линейных непрерывных САУ
Методы математического описания линейных непрерывных САУ Си – простые типы данных, развилки, цикл do while, блок схемы
Си – простые типы данных, развилки, цикл do while, блок схемы Серия игр S.T.A.L.K.E.R
Серия игр S.T.A.L.K.E.R Создание системы информационной безопасности Алматинского районного ЦОНа г. Нур-Султан
Создание системы информационной безопасности Алматинского районного ЦОНа г. Нур-Султан Программирование циклических алгоритмов. Начала программирования
Программирование циклических алгоритмов. Начала программирования