0братная функция

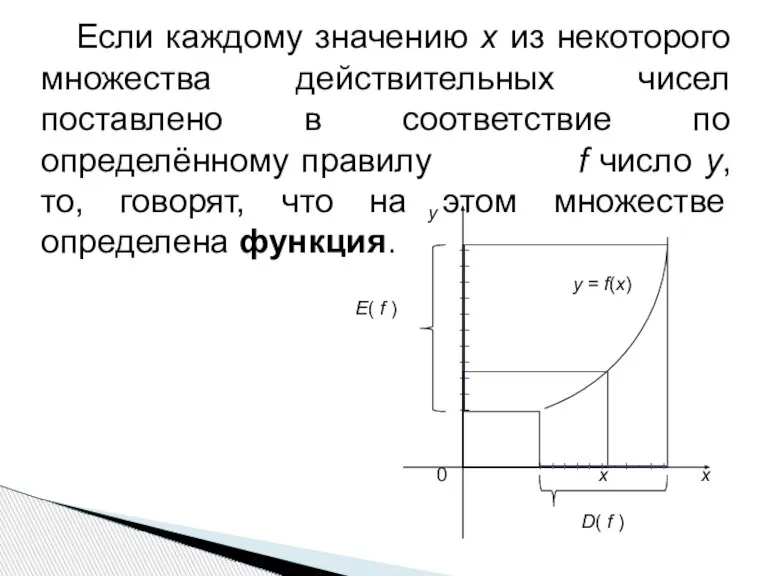
Если каждому значению х из некоторого множества действительных чисел поставлено в соответствие по определённому правилу f число у, то, говорят, что на этом множестве определена функция.

Если функция у = f ( х ) принимает каждое своё значение у только при одном значении х, то эту функцию называют обратимой.

Пусть у = f(x) – обратимая функция. Тогда каждому у из множества значений функции соответствует одно определённое число х из области её определения. Это соответствие определяет функцию х от у, которую обозначим х = g(y).
Поменяем местами х и у: у = g(x).
Функцию у = g(x) называют обратной к функции у = f(x).

Свойства обратных функций
Область определения обратной функции D(g). совпадает с множеством значений исходной E(f), а множество значений обратной функции E(g) совпадает с областью определения исходной функции D(f):
D(f ) = E(g), E(f ) = D(g).
2. Монотонная функция является обратимой.
3. График обратной функции симметричен графику данной функции относительно прямой у = х.

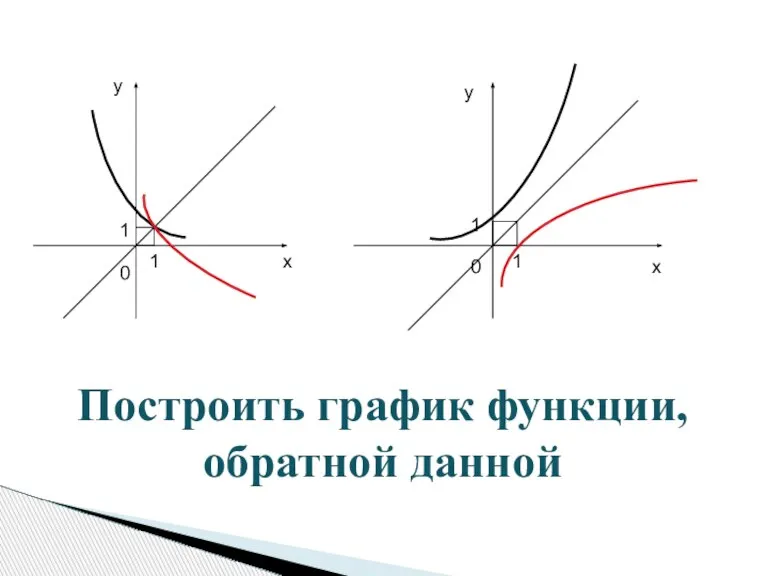
1
1
1
1
0
0
х
у
у
х
Построить график функции, обратной данной

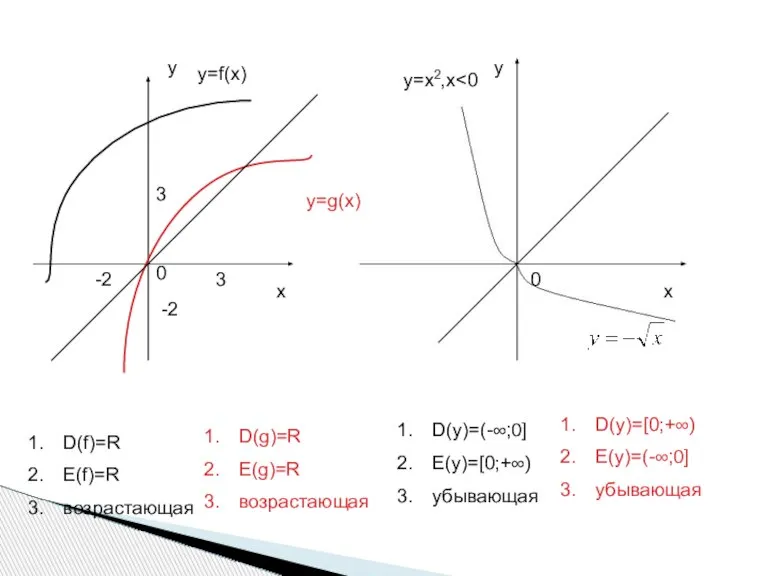
у
х
х
у
0
0
3
3
-2
-2
у=f(x)
у=g(x)
y=x2,х<0
D(f)=R
E(f)=R
возрастающая
D(g)=R
E(g)=R
возрастающая
D(y)=(-∞;0]
E(y)=[0;+∞)
убывающая
D(y)=[0;+∞)
E(y)=(-∞;0]
убывающая

Убедиться в монотонности функции у=f(х). Найти Д(f) и Е(f).
Выразить переменную х через у.
Переобозначить переменные. (Заменить х на у, у на х).
Проверить D(f ) = E(g), E(f ) = D(g).
Построить графики и проверить симметричность относительно прямой у=х
х
у
0
(х0;у0)
х0
у0
(у0;х0)
у = х
Найти функцию, обратную данной:

Нахождение формулы функции, обратной к функции y=f(x)
Пример 1
Пример 2

х
у
0
у = х
Для заданной функции найдите обратную функцию и постройте их графики, проверив их симметричность относительно прямой у= х

Проверка:

Установите соответствие между функцией f(x) и обратной к ней функцией g(x)