Развитие учебных навыков через применение наглядных пособий и перевода математических задач в практическую плоскость

Одной из важнейших проблем преподавания математики в вечерних (сменных) школах является ликвидация пробелов в знаниях учеников по различным разделам школьного курса математики.
Происхождение этих пробелов разное - они образуются в результате пропусков части занятий отдельными учениками (что часто имеет объективные причины - работа в сменах, служебные командировки, выполнение семейных обязанностей), а также и потому, что в вечерние (сменные) школы учащиеся чаще всего поступают после длительного перерыва в учебе. Кроме того, многие из них выбыли из массовых школ именно в связи с наличием больших пробелов в знаниях, в частности, и по математике.
В связи с этим и возникает вопрос, как восстанавливать и развивать учебные навыки учащихся.

Наглядные методы применяются на всех этапах педагогического процесса.
Цель метода наглядности - обогащение и расширение непосредственного, чувственного опыта учеников, развитие наглядности, изучение конкретных свойств предметов, создание условий для перехода к абстрактному мышлению, опоры для самостоятельного учения и систематизации изученного.
Следует понимать, что прочные знания у учащихся будут в том случае, если учитель будет опираться на жизненный опыт ребенка.
На мой взгляд,
наиболее эффективными
являются
наглядные методы обучения.

1) хорошее обозрение, которое достигается путем применения соответствующих красок;
2) четкое выделение главного, основного при показе иллюстраций, так как они порой содержат и отвлекающие моменты;
3) детальное продумывание пояснений (вводных, по ходу показа и заключительных), необходимых для выяснения сущности демонстрационных явлений, а также для обобщения усвоенной учебной информации;
4) привлечение самих учеников к нахождению желаемой информации в наглядном пособии, постановка перед ними проблемных заданий наглядного характера.
Есть несколько методических условий, выполнение которых обеспечивает успешное использование наглядных средств обучения:

Ассоциативные образы помогают прочно усваивать изучаемый материал, быстро вспоминать правило.
Ученикам достаточно назвать ключевое слово, например, «я должен», «у меня есть» как они вспоминают правило сложения чисел с разными знаками.
Этот метод обучения непосредственно стимулирует учение за счет максимально возможной конкретизации знаний.
Одним из действенных приемов стимулирования интереса к учению является создание в учебном процессе ситуаций успеха, которые создаются путем дифференциации помощи школьникам в выполнении учебных заданий одной и той же сложности. Обязательный набор операций в строгой последовательности становится главным условием успеха.
Перечень необходимых действий прост и понятен, поэтому свои силы хочется попробовать многим.

Связь наглядных и словесных методов
Особенностью наглядных методов обучения является то, что они обязательно предполагают в той или иной мере сочетание их со словесными методами.
Учитель руководит наблюдением, которое осуществляется учащимися, а знания об облике объекта, его непосредственно воспринимаемых свойствах и отношениях ученики извлекают из самого наглядного объекта в процессе наблюдений;
на основании наблюдения наглядных объектов и на базе имеющихся у учащихся знаний учитель ведет к осмыслению и формированию связей в явлениях, которые не могут быть высмотрены в процессе восприятия;
наглядные средства служат подтверждением или конкретизацией словесных сообщений; отправляясь от осуществляемого школьниками наблюдения наглядного объекта, учитель сообщает о таких связях между явлениями, которые непосредственно не воспринимаются учащимися, либо делает вывод, объединяет, обобщает отдельные данные.

При составлении наглядного материала необходимо избегать распространенной ошибки – применение очень яркой наглядности, когда ее учебная сущность затмевается яркими красками.
Схемы, таблицы содержат цвет только для выделения смысла, но не для украшения.
Результаты, в реальной практике преподавания достигаются отнюдь не всеми и применение данного метода носит индивидуальный характер.
Риски

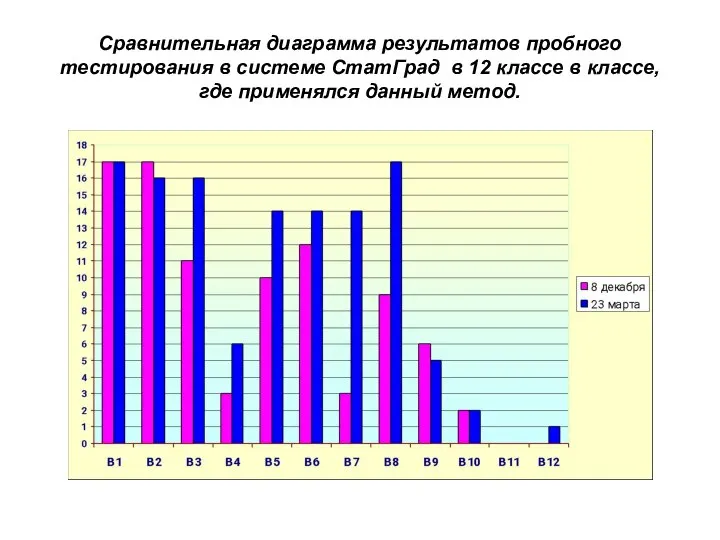
Сравнительная диаграмма результатов пробного тестирования в системе СтатГрад в 12 классе в классе, где применялся данный метод.

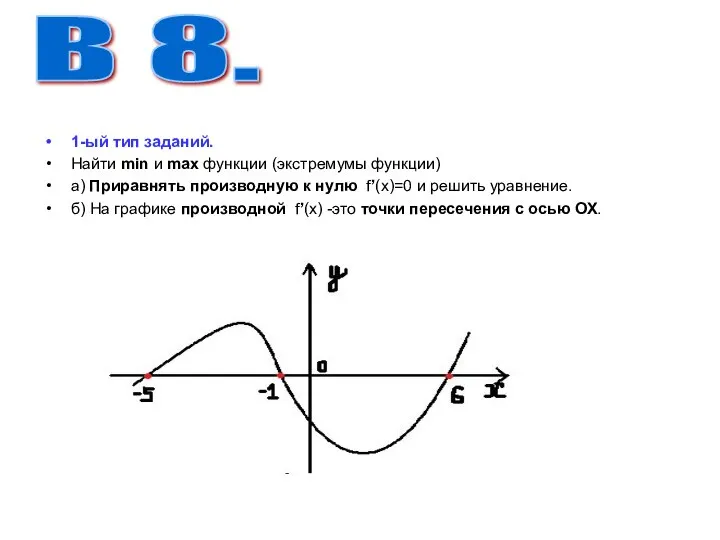
1-ый тип заданий.
Найти min и max функции (экстремумы функции)
а) Приравнять производную к нулю f’(x)=0 и решить уравнение.
б) На графике производной f’(x) -это точки пересечения с осью ОХ.
В 8.

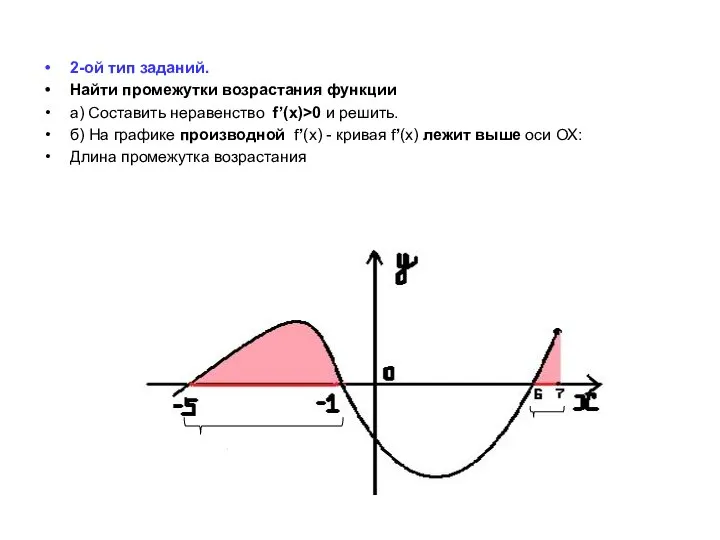
2-ой тип заданий.
Найти промежутки возрастания функции
а) Составить неравенство f’(x)>0 и решить.
б) На графике производной f’(x) - кривая f’(x) лежит выше оси ОХ:
Длина промежутка возрастания

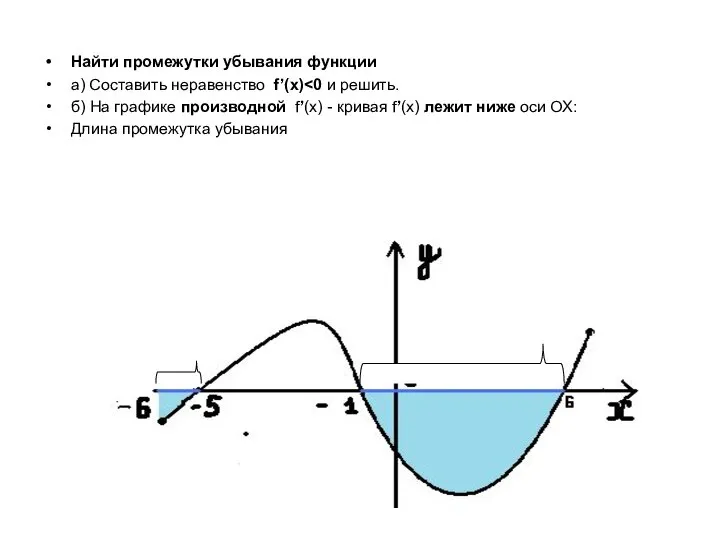
Найти промежутки убывания функции
а) Составить неравенство f’(x)<0 и решить.
б) На графике производной f’(x) - кривая f’(x) лежит ниже оси ОХ:
Длина промежутка убывания

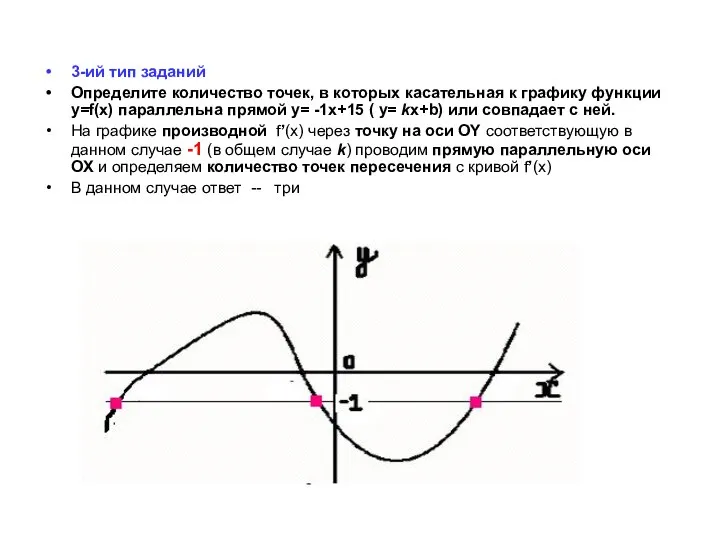
3-ий тип заданий
Определите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y= -1x+15 ( y= kx+b) или совпадает с ней.
На графике производной f’(x) через точку на оси OY соответствующую в данном случае -1 (в общем случае k) проводим прямую параллельную оси OX и определяем количество точек пересечения с кривой f’(x)
В данном случае ответ -- три