Содержание
- 2. 1) Наведіть зразки предметів, що можуть служити моделлю площини. Повторимо: (Стеля, підлога, кришка стола, шибка у
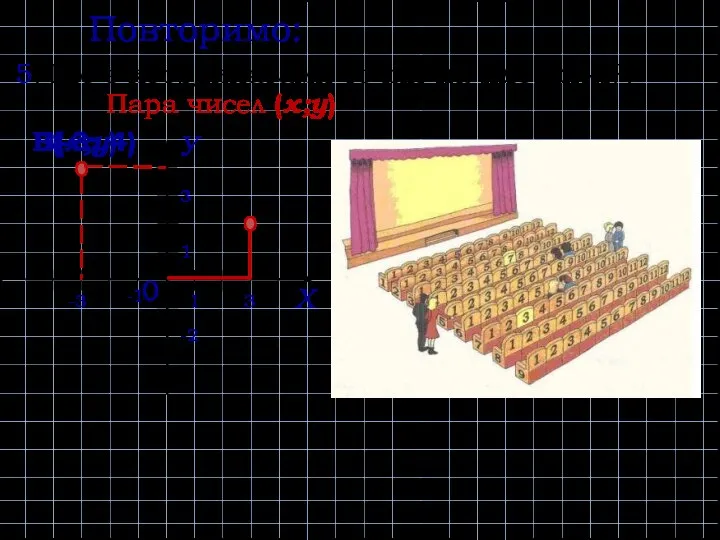
- 3. 5) Що є координатами точки на площині?. Повторимо: Пара чисел (х;у) 0 Х У 1 3
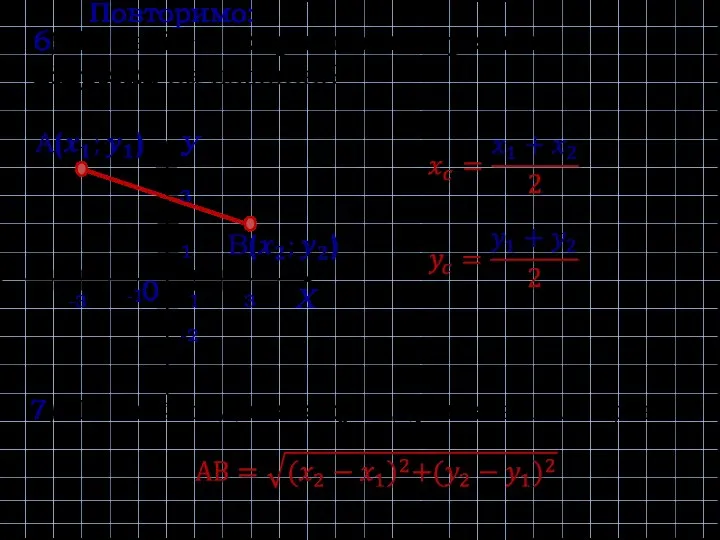
- 4. 6) Як знайти координати середини відрізка на площині? 0 Х У 1 3 1 -1 -2
- 5. 8) Які особливості точок, що лежать на координатних осях? 0 Х У 1 3 1 -1
- 6. 1) Що таке координатний простір? Це простір, в якому задана система координат. 2) А що таке
- 7. Декартові координати у просторі Тема: §24, с. 189 – підручник, 11 кл.
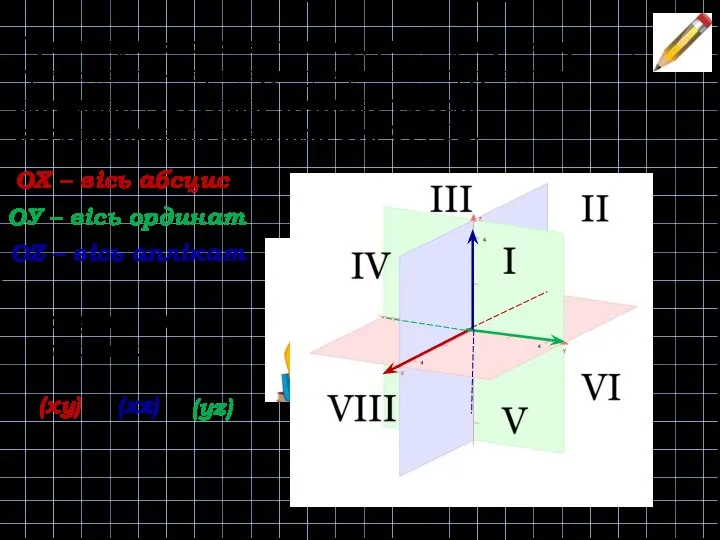
- 8. Прямокутна система координат у просторі – це три взаємно-перпендикулярних координатних площини, утворених попарно трьома координатними прямими
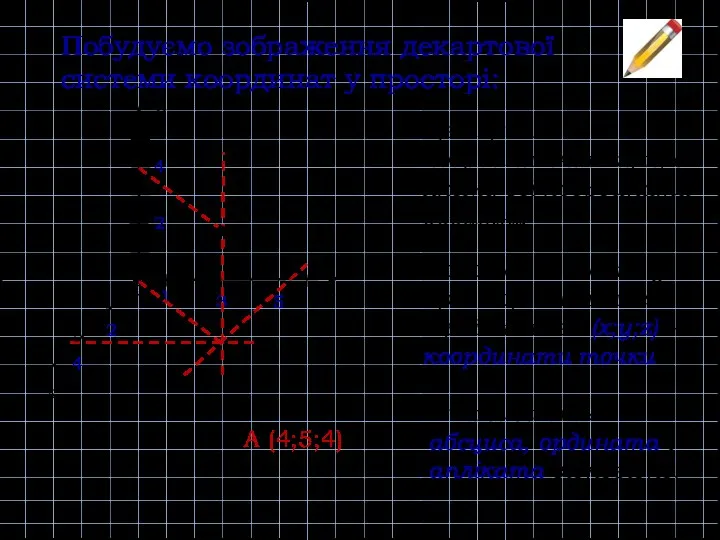
- 9. Побудуємо зображення декартової системи координат у просторі: Х О У Z 1 3 5 2 4
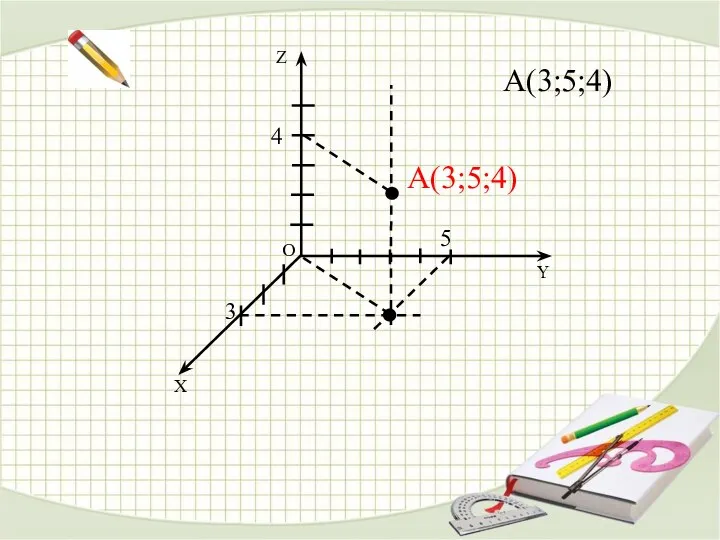
- 10. О Y X Z A(3;5;4) 3 5 4 A(3;5;4)
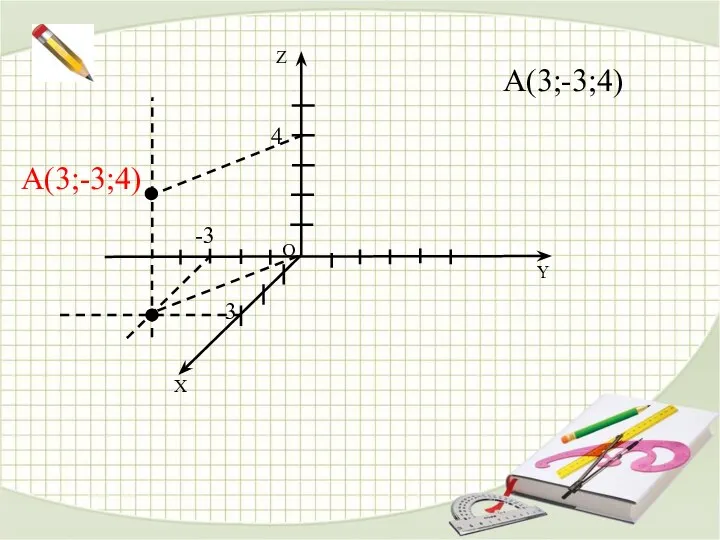
- 11. О Y X Z A(3;-3;4) 3 -3 4 A(3;-3;4)
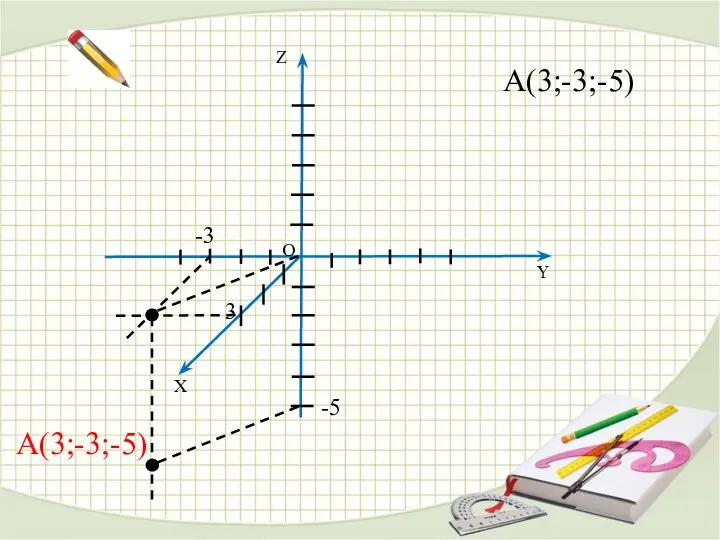
- 12. О Y X Z A(3;-3;-5) 3 -3 -5 A(3;-3;-5)
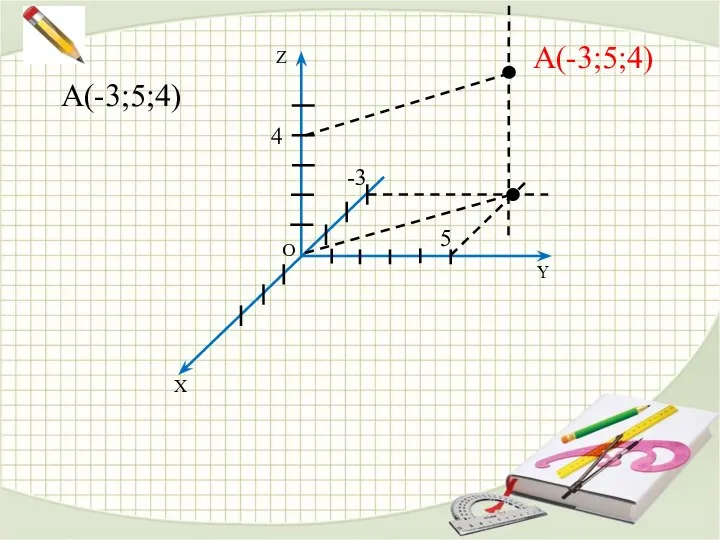
- 13. О Y X Z A(-3;5;4) -3 5 4 A(-3;5;4)
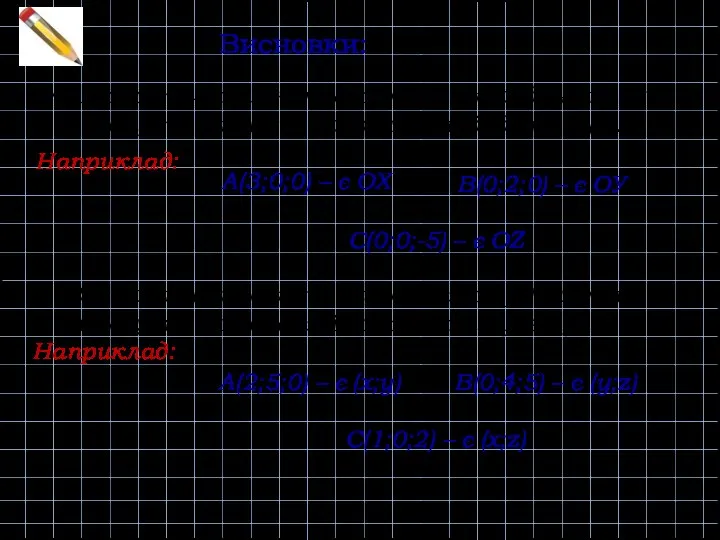
- 14. Висновки: Якщо точка лежить на одній з координатних осей, то дві інші її координати будуть нулі:
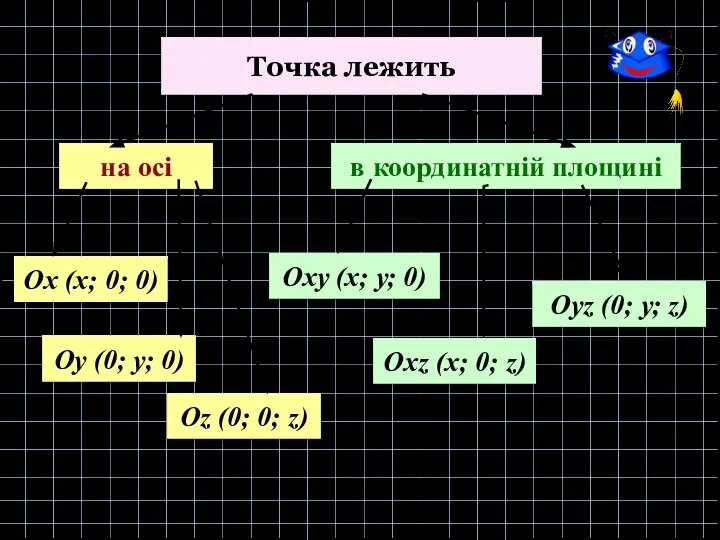
- 15. Точка лежить на осі Оу (0; у; 0) Ох (х; 0; 0) Оz (0; 0; z)
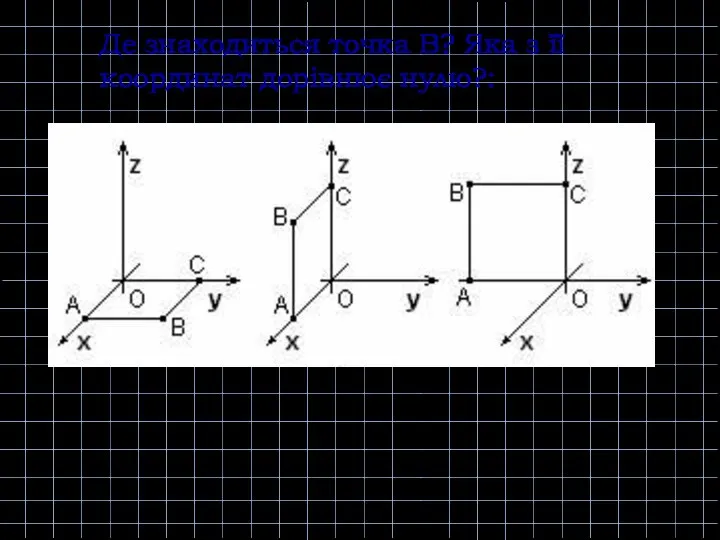
- 16. Де знаходиться точка В? Яка з її координат дорівнює нулю?:
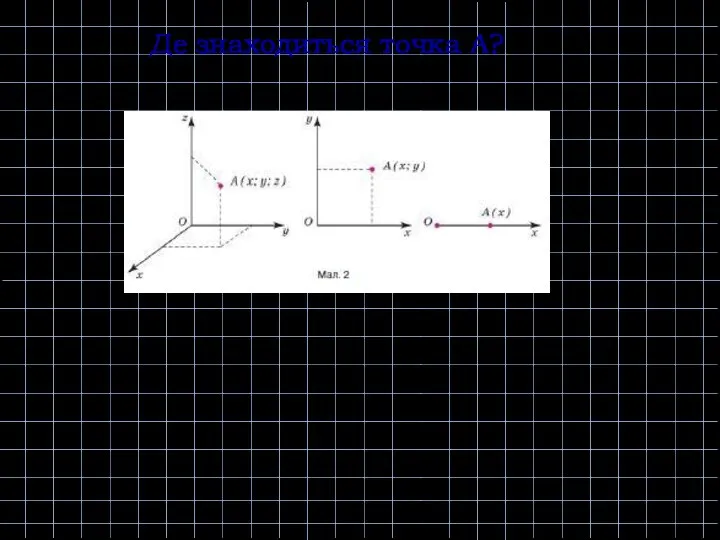
- 17. Де знаходиться точка А?
- 18. Координати середини відрізка: Відстань між точками (довжина відрізка):
- 20. Скачать презентацию





 Геометрическая прогрессия
Геометрическая прогрессия Логические операции И ИЛИ
Логические операции И ИЛИ Уравнения. Графики
Уравнения. Графики Параллельные прямые
Параллельные прямые Интегрированный урок математики и чтения в 5 классе. Басни И.А.Крылова
Интегрированный урок математики и чтения в 5 классе. Басни И.А.Крылова Смежные и вертикальные углы
Смежные и вертикальные углы Перпендикуляр и наклонная
Перпендикуляр и наклонная Построение сечения многогранника плоскостью
Построение сечения многогранника плоскостью Метод научного познания: измерение. Процедура измерения
Метод научного познания: измерение. Процедура измерения Умножение дробей
Умножение дробей Логика и логические задачи
Логика и логические задачи Линейная функция
Линейная функция Арифметический диктант
Арифметический диктант Խնդիր Հաշվել a, b, c կողմեր ունեցող եռանկյան մակերեսը
Խնդիր Հաշվել a, b, c կողմեր ունեցող եռանկյան մակերեսը Презентация на тему Уменьшаемое. Вычитаемое. Значение разности
Презентация на тему Уменьшаемое. Вычитаемое. Значение разности  Координаты и векторы
Координаты и векторы Площа криволінійної трапеції
Площа криволінійної трапеції Урок математики. Замени произведение суммой
Урок математики. Замени произведение суммой Презентация на тему ГИА 2013. Модуль АЛГЕБРА (№8)
Презентация на тему ГИА 2013. Модуль АЛГЕБРА (№8)  Векторы. Векторные и скалярные величины
Векторы. Векторные и скалярные величины Треугольник. Периметр треугольника. 9 класс
Треугольник. Периметр треугольника. 9 класс Теорема Пифагора
Теорема Пифагора Подготовка к ВПР по математике
Подготовка к ВПР по математике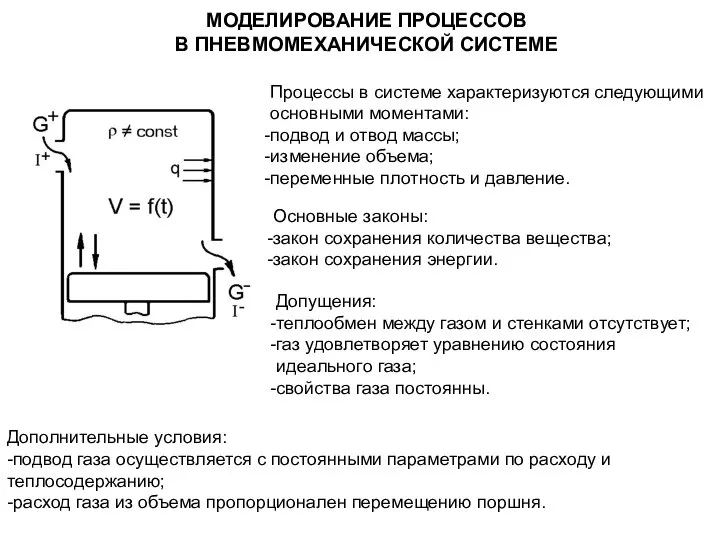 Моделирование процессов в пневмомеханической системе
Моделирование процессов в пневмомеханической системе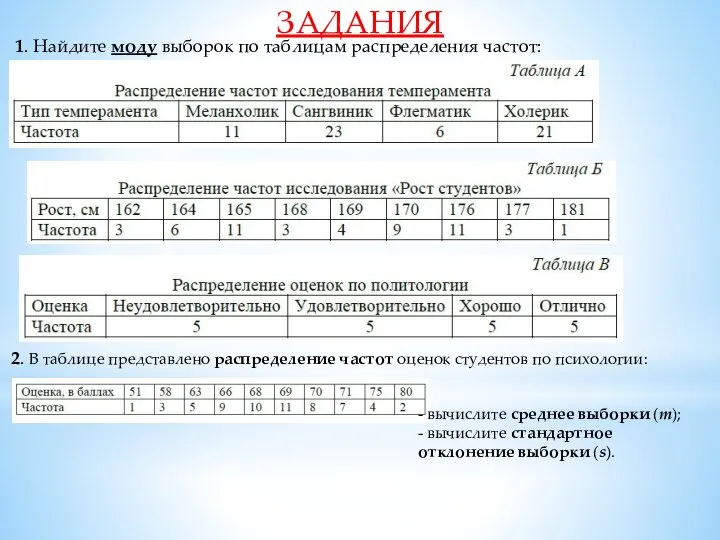 Математические методы
Математические методы Презентация на тему Первый признак равенства треуголников
Презентация на тему Первый признак равенства треуголников  Отношения величины поверхности к объему
Отношения величины поверхности к объему Базис и координаты
Базис и координаты