1-2_1

На платформе разместите 4 столба так, чтобы их верхние точки образовывали плоскость (чтобы можно было перевернуть данную модель и все четыре столба касались поверхности пола). – МОДЕЛЬ СТОЛА
Эксперимент

2.3 Прямая k пересекает стороны параллелограмма в двух точках. Верно ли, что прямая k лежит на плоскости параллелограмма?
2.4 Верно ли, что прямая лежит на плоскости, если две ее точки лежат на этой плоскости? Обоснуй свой ответ.
2.5 Концы диаметра окружности лежат на плоскости α. Верно ли, что все точки окружности принадлежат плоскости α?

Рассмотрим следующие теоремы,
которые являются следствиями из аксиом стереометрии.
Теорема 1. Через прямую и точку, не принадлежащую ей, можно провести плоскость, и притом только одну.
Доказательство:
1. По условию B∉c.
2. Отметим на прямой c точки K и E, значит, K, E∈C.
3. Точки B, K, E не лежат на одной прямой, следовательно, по аксиоме С1 можно провести плоскость α (B∈α, K∈α, E∈α).
4. Точки K, E лежат на прямой с, значит, по Аксиоме С3:
c⸦α. Следовательно, плоскость α проходит через точку B и прямую c.
5. Единственность плоскости, проходящей через прямую c и точку B, следует из того, что любая плоскость, проходящая через прямую c и точку B, проходит через точки B, K, E. Следовательно, данная плоскость совпадает с плоскостью α, т.к.
по аксиоме С1 через точки B, K и E проходит только одна плоскость.

Теорема 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Доказательство:
1. По условию a ∩ c = K (K ∈ a, K ∈ c).
2. Е — некоторая точка на прямой a (E∈α) не совпадающей
точкой K.
3. Следовательно, по теореме 1 существует плоскость α, прохо-
дящая через точку Е и прямую a.

2.6 Докажи, что через две пересекающиеся прямые проходит единственная плоскость.
2.7 Диагонали прямоугольника лежат в плоскости α. Лежат ли вершины прямоугольника в плоскости α?
2.8 Выбери верные утверждения (рис. 1).
1. Точки K, E, B лежат на одной прямой.
2. Точки K, E, D лежат на одной прямой.
3. Точки A, E, C лежат на одной прямой.
4. Точки K, E, B лежат на одной плоскости.
5. Точки T, E, B лежат на одной плоскости.
6. Точки K, C, D лежат на одной плоскости.
7. Точки E, B, D лежат на одной плоскости.
8. Прямые KB и AC пересекаются в точке E.
9. Прямая AC пересекается с плоскостью в точке E.

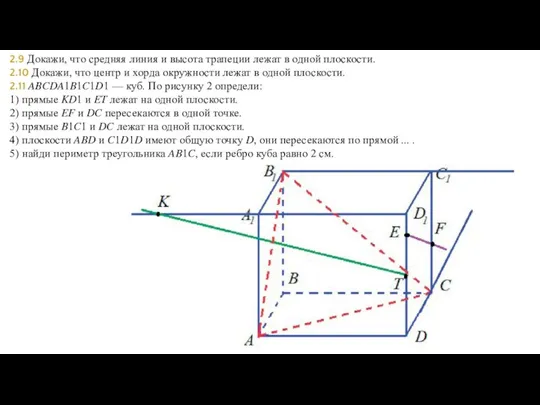
2.9 Докажи, что средняя линия и высота трапеции лежат в одной плоскости.
2.10 Докажи, что центр и хорда окружности лежат в одной плоскости.
2.11 ABCDA1B1C1D1 — куб. По рисунку 2 определи:
1) прямые KD1 и ET лежат на одной плоскости.
2) прямые EF и DC пересекаются в одной точке.
3) прямые B1C1 и DC лежат на одной плоскости.
4) плоскости ABD и C1D1D имеют общую точку D, они пересекаются по прямой ... .
5) найди периметр треугольника AB1C, если ребро куба равно 2 см.

2.12 Две прямые a и b пересекаются в точке N. Докажи, что все прямые, не проходящие через точку N и пересекающие данные прямые, лежат в одной плоскости. Лежат ли в одной плоскости все прямые, проходящие через точку N?
2.13 Одна сторона и точка пересечения диагоналей параллелограмма лежат в одной плоскости α.
Ответь на вопросы и обоснуй их.
1. Лежат ли вершины параллелограмма на плоскости α?
2. Лежат ли прямые, проходящие через середины сторон параллелограмма, на плоскости α?
3. Лежат ли прямые, проходящие через точку пересечения диагоналей параллелограмма, на
плоскости α.

2.14 Выполни чертеж и запиши краткую математическую запись утверждений.
1. Прямая KT лежит на плоскости α.
2. Прямая KT пересекает плоскость α.
3. Прямые PC и PB пересекают плоскость α в одной и той же точке.
4. Прямые PC и PB пересекают плоскость α в разных точках.
5. Плоскости α и β пересекаются по прямой с, плоскости α и γ также пересекаются по этой
же прямой с.
6. Плоскости α и β пересекаются по прямой АВ, а плоскости α и γ пересекаются по другой прямой АС.
7. Плоскость α проходит через прямую а и точку А, не лежащую на прямой а, и пересекает
прямую b в точке А.

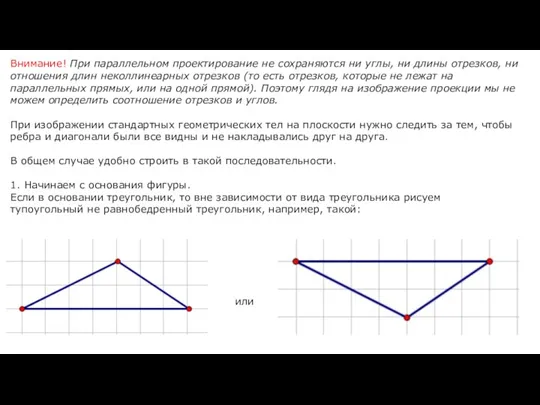
Внимание! При параллельном проектирование не сохраняются ни углы, ни длины отрезков, ни отношения длин неколлинеарных отрезков (то есть отрезков, которые не лежат на параллельных прямых, или на одной прямой). Поэтому глядя на изображение проекции мы не можем определить соотношение отрезков и углов.
При изображении стандартных геометрических тел на плоскости нужно следить за тем, чтобы ребра и диагонали были все видны и не накладывались друг на друга.
В общем случае удобно строить в такой последовательности.
1. Начинаем с основания фигуры.
Если в основании треугольник, то вне зависимости от вида треугольника рисуем тупоугольный не равнобедренный треугольник, например, такой:
или

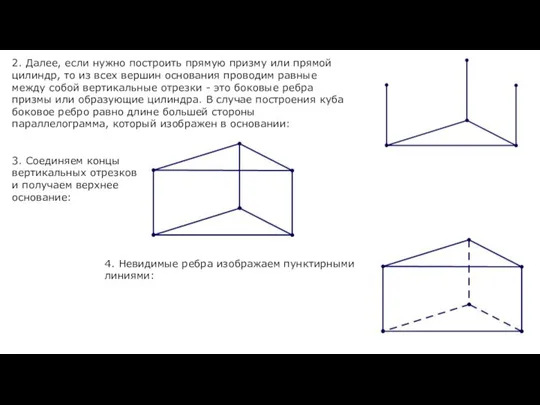
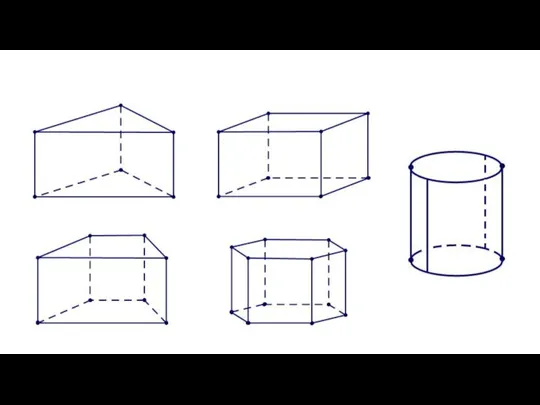
2. Далее, если нужно построить прямую призму или прямой цилиндр, то из всех вершин основания проводим равные между собой вертикальные отрезки - это боковые ребра призмы или образующие цилиндра. В случае построения куба боковое ребро равно длине большей стороны параллелограмма, который изображен в основании:
3. Соединяем концы вертикальных отрезков и получаем верхнее основание:
4. Невидимые ребра изображаем пунктирными линиями:

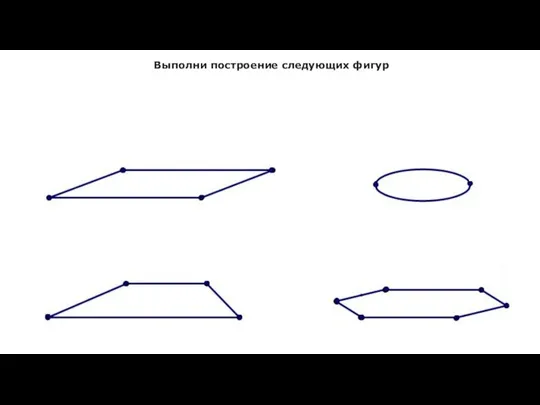
Выполни построение следующих фигур

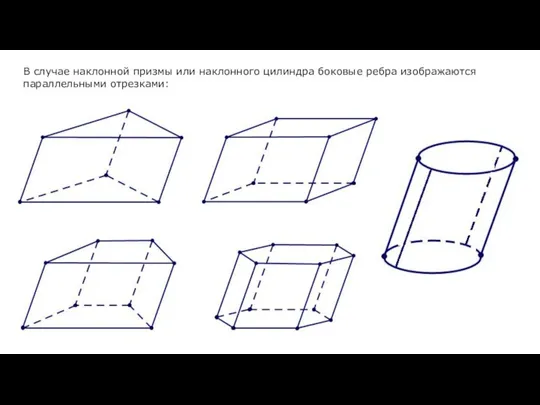
В случае наклонной призмы или наклонного цилиндра боковые ребра изображаются параллельными отрезками:

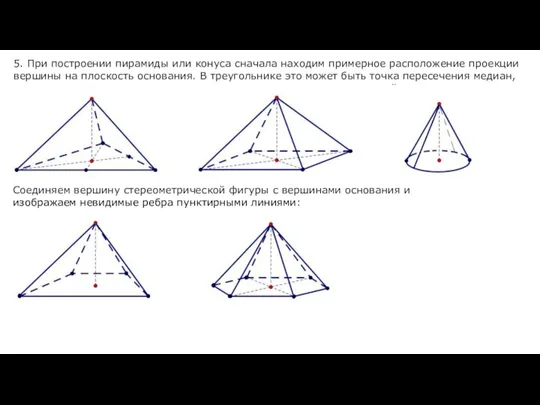
5. При построении пирамиды или конуса сначала находим примерное расположение проекции вершины на плоскость основания. В треугольнике это может быть точка пересечения медиан, в прямоугольнике или шестиугольнике - точка пересечения диагоналей:
Из центра основания проводим вертикальную линию и ставим на ней точку, которая будет вершиной стереометрический фигуры:
Соединяем вершину стереометрической фигуры с вершинами основания и изображаем невидимые ребра пунктирными линиями: