Содержание
- 2. Определение параметров уравнения регрессии с помощью метода наименьших квадратов
- 3. При использовании МНК к ошибкам предъявляются следующие требования, называемые условиями Гаусса - Маркова: 1) величина является
- 4. Критерии значимости коэффициентов и в уравнении регрессии. Коэффициент детерминации .
- 5. При оценке значимости коэффициента линейной регрессии можно использовать следующее грубое правило. Если стандартная ошибка коэффициента больше
- 6. Коэффициент детерминации характеризует долю вариации (разброса) зависимой переменной, объясненной с помощью данного уравнения. В качестве меры
- 7. Иногда при расчете коэффициента детерминации для получения несмещенных оценок дисперсии в числителе и знаменателе вычитаемой из
- 8. Для определения статистической значимости коэффициента детерминации проверяется нулевая гипотеза для F-статистики, рассчитываемой по формуле: Величина F,
- 9. Гетероскедастичность. Если остатки имеют постоянную дисперсию, они называются гомоскедастичными, но если они непостоянны, то гетероскедастичными. Гетероскедастичность
- 10. Гетероскедастичность Критерий Голдфелда-Кванта - это отношение суммы квадратов отклонений (СКО) высоких остатков к СКО низких остатков:
- 11. Автокорреляция.
- 12. Автокорреляция Автокорреляция, также известная как сериальная корреляция, имеет место, когда остатки не являются независимыми друг от
- 13. Мультиколлинеарность Если некоторые или все независимые переменные в множественной регрессии являются высоко коррелированными, то регрессионной модели
- 14. Для уменьшения мультиколлинеарности может быть принято несколько мер: Увеличивают объем выборки по принципу, что больше данных
- 15. Фиктивные переменные Иногда необходимо включение в регрессионную модель одной или более качественных переменных, например, степени качества
- 16. Нелинейная регрессия. Интервал прогнозирования:
- 17. Выявление наличия корреляционной связи между парой показателей и оценка ее тесноты. линейный (парный) коэффициент корреляции: Для
- 18. Оценка значимости коэффициента корреляции при малых объемах выборки выполняется с использованием t-критерия Стьюдента. При этом фактическое
- 19. Линейный коэффициент корреляции изменяется в пределах от -1 до +1. Его положительные значения свидетельствуют о прямой
- 20. Вычисленное по этой формуле значение tнабл сравнивается с критическим значением t-критерия, которое берется из таблицы значений
- 21. Матрица коэффициентов парной корреляции
- 22. Анализ матрицы коэффициентов парной корреляции используют при построении моделей множественной регрессии. Одной корреляционной матрицей нельзя полностью
- 23. Множественный коэффициент корреляции
- 24. Решение первой задачи (определение тесноты связи одной случайной величины с совокупностью остальных величин, включенных в анализ)
- 25. Частный коэффициент корреляции Если рассматриваемые случайные величины коррелируют друг с другом, то на величине коэффициента парной
- 26. Частный коэффициент корреляции
- 28. Скачать презентацию

























 Действия с функциями (9 задание ЕГЭ)
Действия с функциями (9 задание ЕГЭ) Математическая модель игры World of Tanks
Математическая модель игры World of Tanks преобразование графиков (1)
преобразование графиков (1) Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика
Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика Элементы теории вероятностей
Элементы теории вероятностей predel_funktsii
predel_funktsii Симметрия в природе и в жизни
Симметрия в природе и в жизни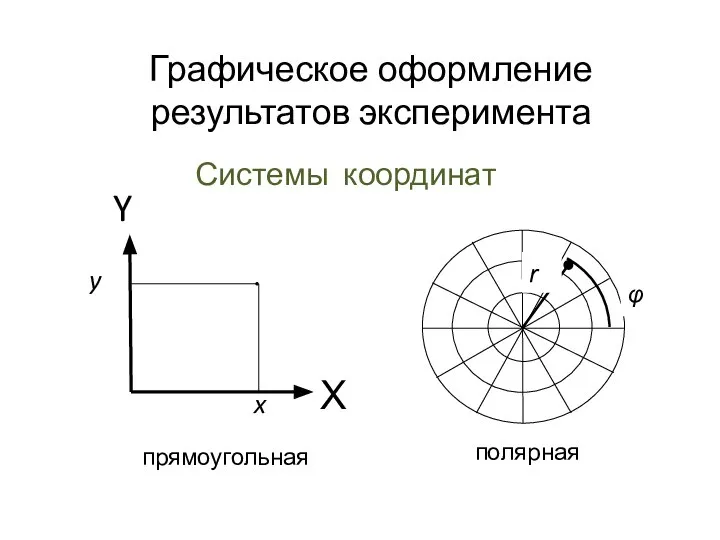 Графическое оформление результатов эксперимента
Графическое оформление результатов эксперимента Задачи. Геометрия 8 кл
Задачи. Геометрия 8 кл Объемы многогранников и тел вращения. Устная работа
Объемы многогранников и тел вращения. Устная работа Стародубцева Анна 9-а класс
Стародубцева Анна 9-а класс Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Свойства квадратного корня
Свойства квадратного корня Подобие треугольников
Подобие треугольников Школа волшебников
Школа волшебников Сосчитай-ка, угадай-ка. 4 класс
Сосчитай-ка, угадай-ка. 4 класс Основные тригонометрические формулы
Основные тригонометрические формулы Определители
Определители Разные задачи. Способ Пропорция
Разные задачи. Способ Пропорция Алгебра. Дроби. Сумма дробей
Алгебра. Дроби. Сумма дробей Применение мультимедийных презентаций для организации устных упражнений на уроках математики в 5-6 классах. Модуль 1
Применение мультимедийных презентаций для организации устных упражнений на уроках математики в 5-6 классах. Модуль 1 Решение иррациональных уравнений
Решение иррациональных уравнений Тригонометрические уравнения. Арксинус
Тригонометрические уравнения. Арксинус Задание 7. Простейшие текстовые задачи
Задание 7. Простейшие текстовые задачи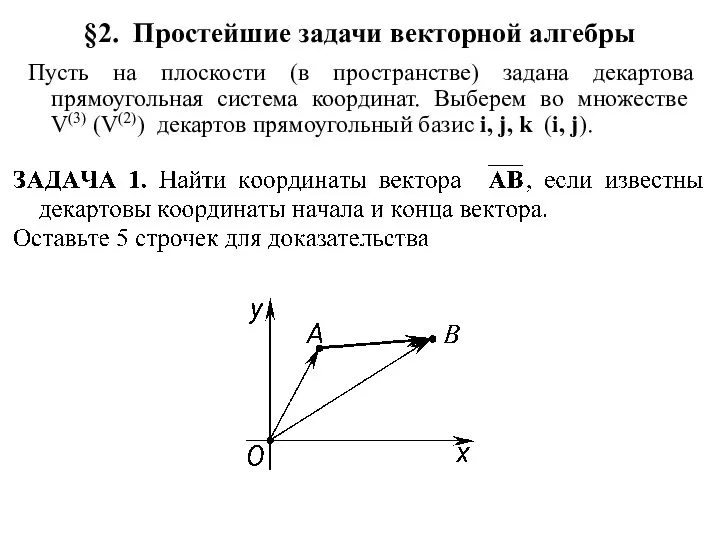 Простейшие задачи векторной алгебры
Простейшие задачи векторной алгебры Группировка слагаемых
Группировка слагаемых Урок математики 4 класс Тема: «Письменное умножение на числа, оканчивающиеся нулями» МБУО «Новообинцевская средняя общеобразова
Урок математики 4 класс Тема: «Письменное умножение на числа, оканчивающиеся нулями» МБУО «Новообинцевская средняя общеобразова Система географических координат
Система географических координат