Слайд 2Решаем задачи:
№№ 344, 345, 348, 350
Комментарии к упражнениям.
№355 - повторение

Слайд 3№344
16
9
Взаимное расположение окружности и прямой определяется соотношением радиуса окружности и расстояния от

центра окружности до прямой. В этой задаче речь идет о координатных осях и о прямой параллельной координатной оси. Вспомним , что расстояние от точки до координатных осей равно соответствующим координатам этой точки, а до прямой, параллельной оси абсцисс, - разности ординат любой точки этой прямой и данной точки.
Слайд 4№345
Уравнение фигуры является уравнением окружности, если его можно представить в виде
Образец

решения этой задачи приведен в задаче 2 данного параграфа.
Слайд 5№348
Расстояние от искомого центра окружности до каждой из данных точек равно данному
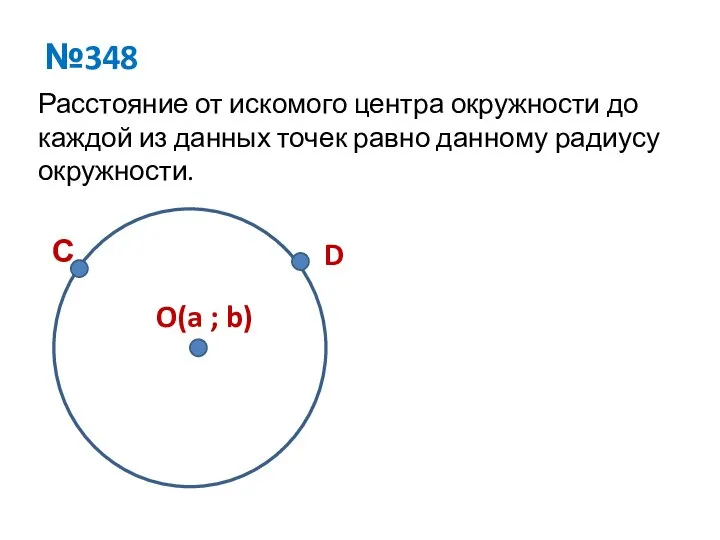
радиусу окружности.
С
D
O(a ; b)
Слайд 6№350
Если окружность касается двух параллельных прямых, то ее диаметр равен расстоянию между

этими прямыми, а центр находится на прямой, лежащей между этими прямыми и находящейся на одинаковом расстоянии от них. Следовательно радиус этой окружности равен ..? И т.д. Подумайте: сколько окружностей удовлетворяет данным условиям расположения?
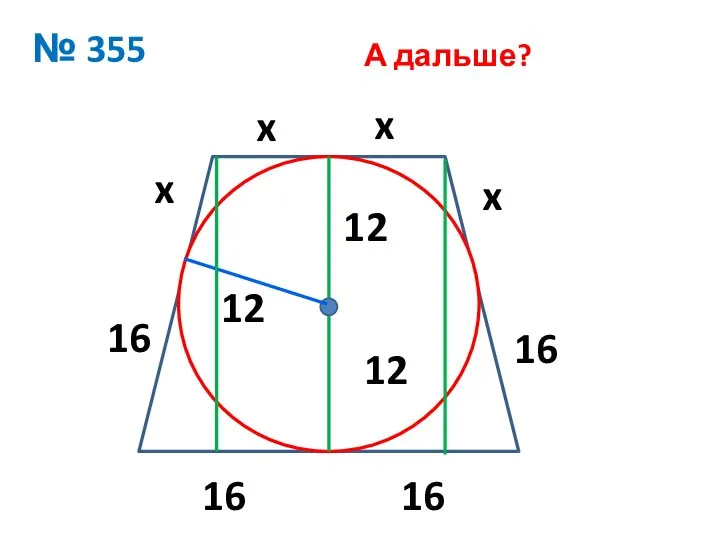
Слайд 7№ 355
16
16
16
16
12
12
x
x
x
x
12
А дальше?






 Знакомство с линиями чертежа Замкнутая, незамкнутая
Знакомство с линиями чертежа Замкнутая, незамкнутая Презентация по математике "Решение задач с помощью систем уравнений второй степени" -
Презентация по математике "Решение задач с помощью систем уравнений второй степени" -  Площадь прямоугольника
Площадь прямоугольника Геометрическая прогрессия
Геометрическая прогрессия Производная функции
Производная функции Числоа 6, 7. Письмо цифры 6
Числоа 6, 7. Письмо цифры 6 Измерительные работы
Измерительные работы Своя игра 1
Своя игра 1 Решение уравнений и неравенств заданий С3
Решение уравнений и неравенств заданий С3 Неопределенный интеграл
Неопределенный интеграл Пустое множество
Пустое множество Методы отбора единиц наблюдения для выборочной совокупности. Возможные типы систематических ошибок оценки в исследованиях
Методы отбора единиц наблюдения для выборочной совокупности. Возможные типы систематических ошибок оценки в исследованиях Подготовка к ПА
Подготовка к ПА Асимптотические методы. Граничные условия на горизонтальной скважине. (Лекция 3)
Асимптотические методы. Граничные условия на горизонтальной скважине. (Лекция 3) Математический диктант
Математический диктант Математическая статистика
Математическая статистика Математический турнир Степень и ее свойства. 7 класс
Математический турнир Степень и ее свойства. 7 класс Тригонометрические функции
Тригонометрические функции Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Дифференциальное исчисление функций нескольких переменных
Дифференциальное исчисление функций нескольких переменных Линейное уравнение с двумя переменными
Линейное уравнение с двумя переменными krivye-vtorogo-poryadka (1)
krivye-vtorogo-poryadka (1) Геометрический и физический смысл производной. Решение задач
Геометрический и физический смысл производной. Решение задач Основное свойство дроби
Основное свойство дроби Информационная безопасность. Базовые логические элементы, применяемые в вычислительной технике
Информационная безопасность. Базовые логические элементы, применяемые в вычислительной технике Круги Эйлера в решении задач
Круги Эйлера в решении задач Учимся писать цифры
Учимся писать цифры