АЛГОРИТМ ЕВКЛИДА

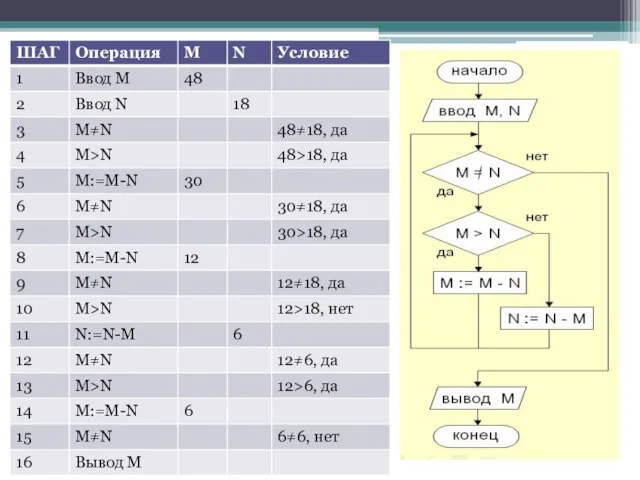
АЛГОРИТМ ЕВКЛИДА
Алгоритм Евклида - это алгоритм нахождения наибольшего общего делителя (НОД) двух целых неотрицательных чисел.
Евклид
(365-300 до. н. э.)
Древнегреческие математики называли этот алгоритм ἀνθυφαίρεσις или ἀνταναίρεσις — «взаимное вычитание».

Вычисление НОД
НОД = наибольший общий делитель двух натуральных чисел – это наибольшее число, на которое оба исходных числа делятся без остатка.
НОД(a, b)= НОД(a-b, b)= НОД(a, b-a)
Заменяем большее из двух чисел разностью большего и меньшего до тех пор, пока они не станут равны. Это и есть НОД.
НОД (18, 45) = НОД (18, 45-18) = НОД (18, 27)= НОД (18, 9) = =НОД(9,9)=9
Пример :

program Evklid;
var m, n: integer;
begin
writeln ('vved 2 chisla');
readln (m,n);
while m<>n do begin
if m>n
then m:=m-n
else n:=n-m;
end;
write ('nod=',m);
readln
end.

0.Выполните на компьютере программу Evklid. Протестируйте её при значениях М=32, N=24; M=696, N=234.
1. Проверить, являются ли два данных числа взаимно простыми.
Примечание. Два числа называются взаимно простыми, если их наибольший общий делитель равен 1.
2. Найти наименьшее общее кратное (НОК) чисел n и m, если
НОК(n, m) = n * m / НОД (n, m).
3. Даны натуральные числа m и n. Найти такие натуральные p и q, не имеющие общих делителей, что
p / q = m / n.
4. Найти НОД трех чисел.
Примечание. НОД(a, b, c)= НОД(НОД(a, b), c)
Задачи