Содержание
- 2. Цель урока: 10.4.1.1 - знать определение и способы задания функции; 10.4.1.2 - уметь выполнять преобразования графика
- 3. Функция – зависимость при которой, каждому значению величины Х (аргумента) соответствует единственное значение величины У (функции).
- 5. Определение: Функцией называют зависимость, где каждому элементу х из множества определения функции X ставят в соответствие
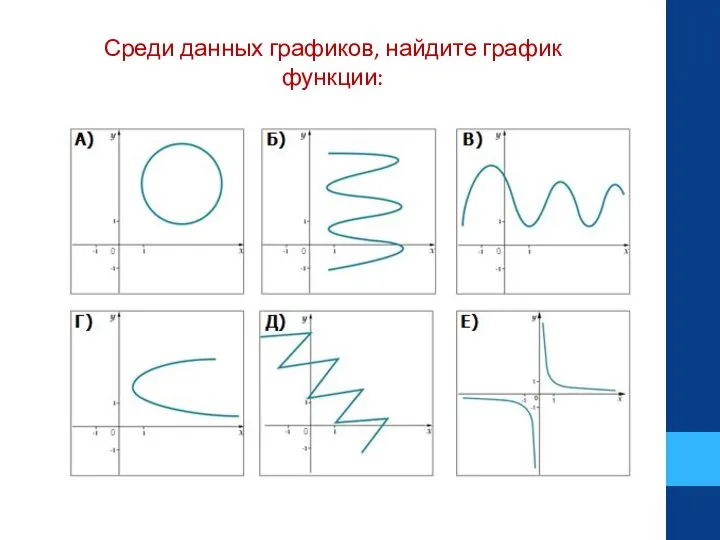
- 6. Среди данных графиков, найдите график функции:
- 8. Способы задания функции АНАЛИТИЧЕСКИЙ ГРАФИЧЕСКИЙ ТАБЛИЧНЫЙ СЛОВЕСНЫЙ
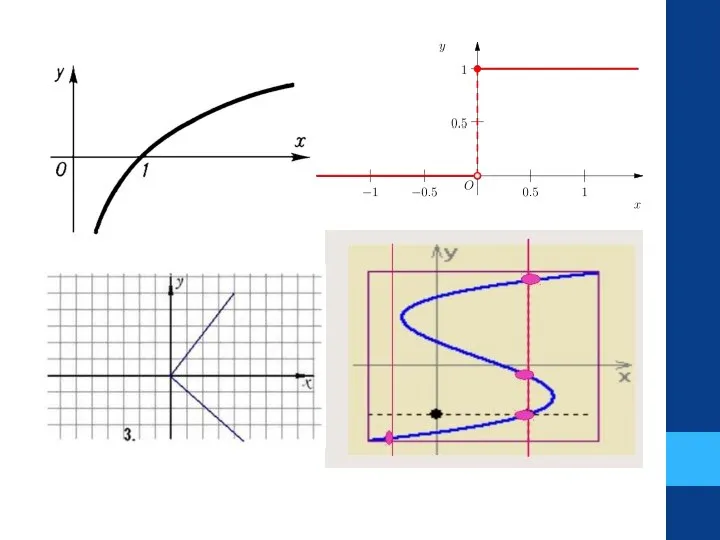
- 9. Способы задания функции АНАЛИТИЧЕСКИЙ функция задается при помощи формулы или нескольких формул Например,
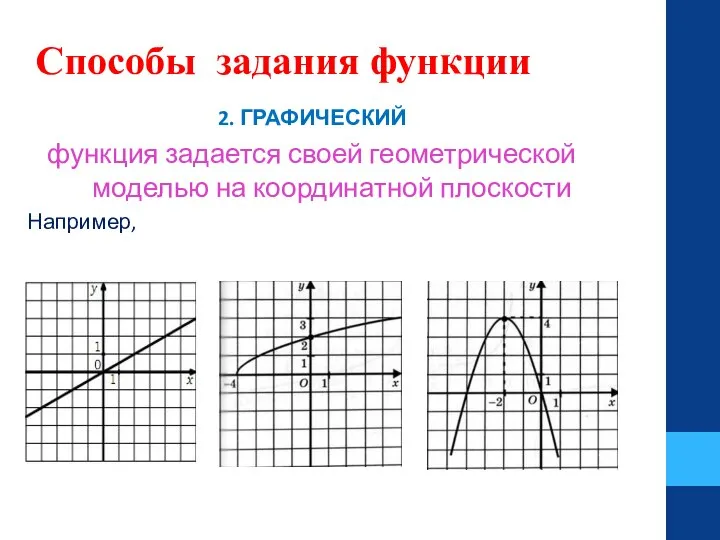
- 10. Способы задания функции 2. ГРАФИЧЕСКИЙ функция задается своей геометрической моделью на координатной плоскости Например,
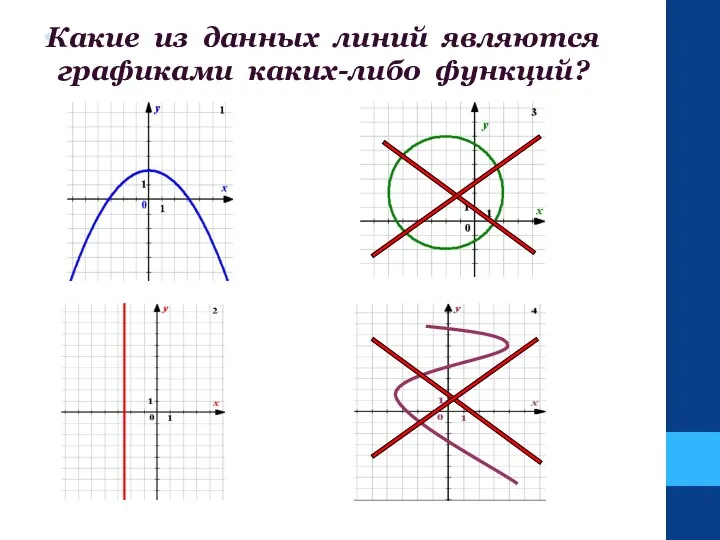
- 11. . Какие из данных линий являются графиками каких-либо функций?
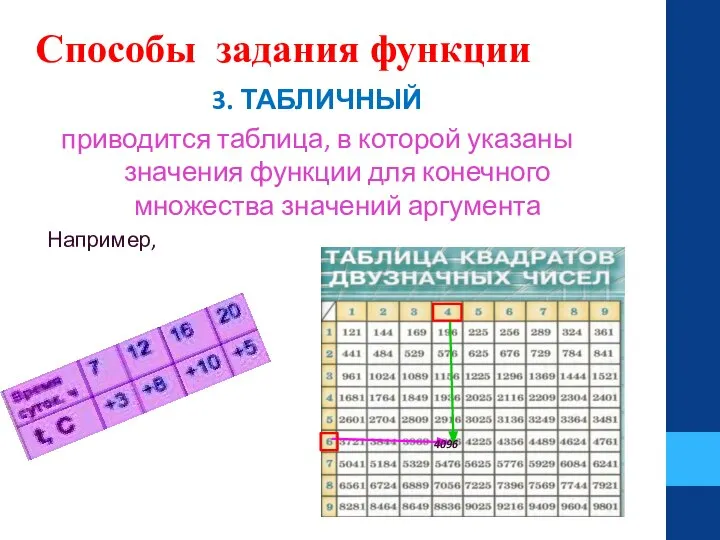
- 12. Способы задания функции 3. ТАБЛИЧНЫЙ приводится таблица, в которой указаны значения функции для конечного множества значений
- 13. Способы задания функции 4. СЛОВЕСНЫЙ правило задания функции описывается словами Например, Каждому натуральному числу ставится в
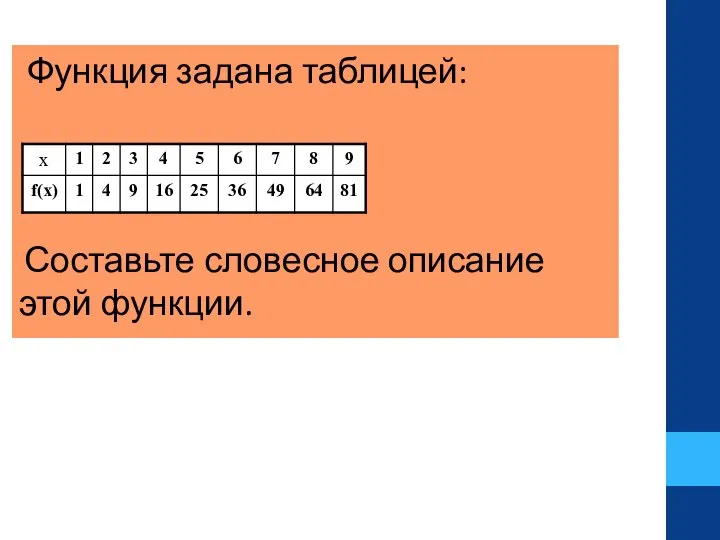
- 14. Функция задана таблицей: Составьте словесное описание этой функции.
- 15. Преобразование графиков функции
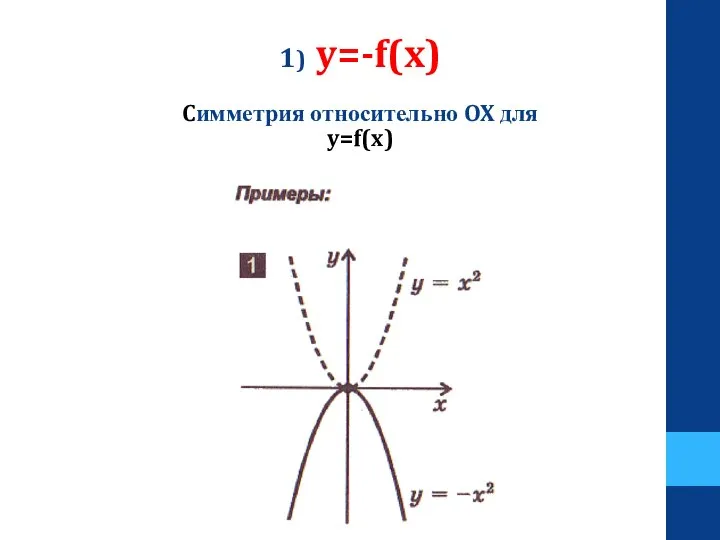
- 16. 1) y=-f(x) Cимметрия относительно OX для y=f(x)
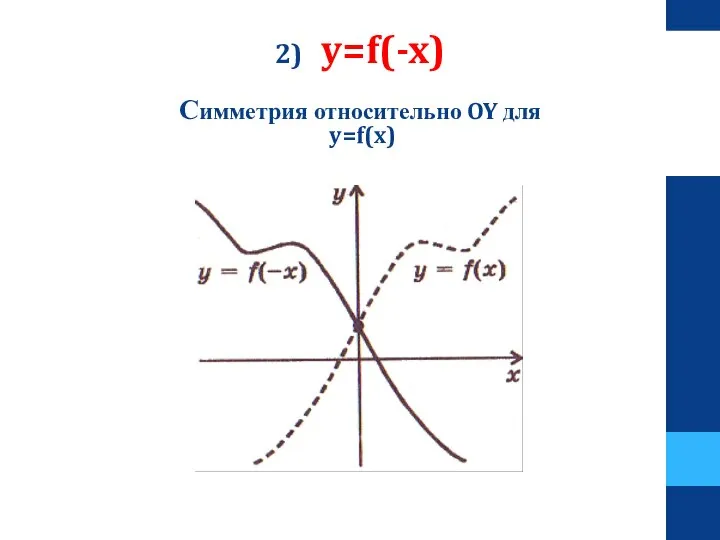
- 17. 2) y=f(-x) Симметрия относительно OY для y=f(x)
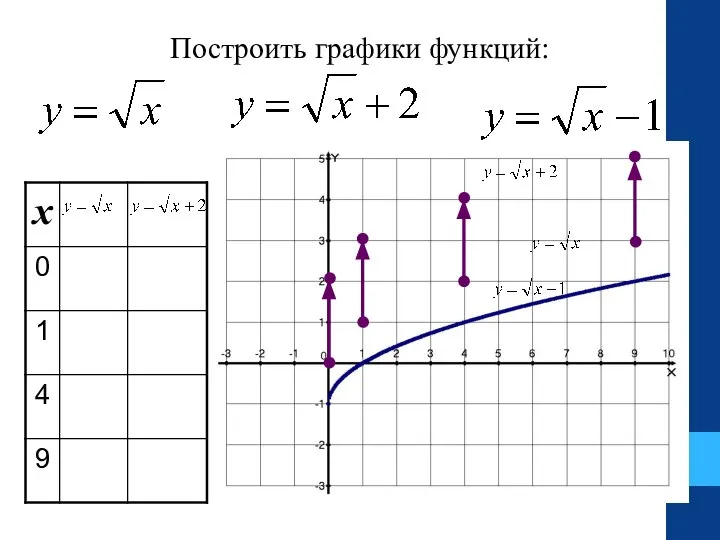
- 18. Построить графики функций:
- 19. График функции получен в результате параллельного переноса графика функции на 2 единицы вверх. График функции получен
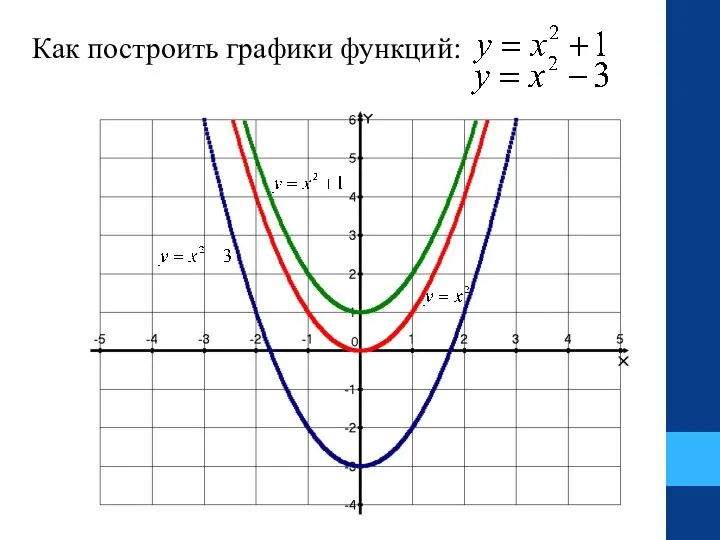
- 20. Как построить графики функций:
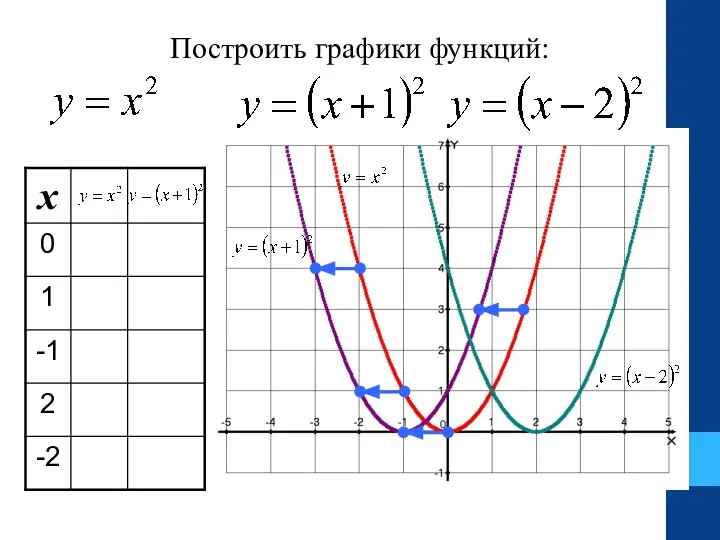
- 21. Построить графики функций:
- 22. График функции получен в результате параллельного переноса графика функции на 1 единицу влево. График функции получен
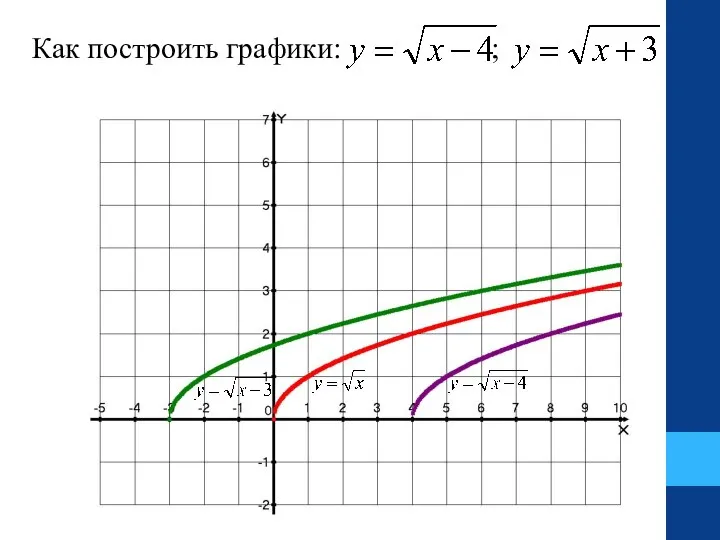
- 23. Как построить графики: ;
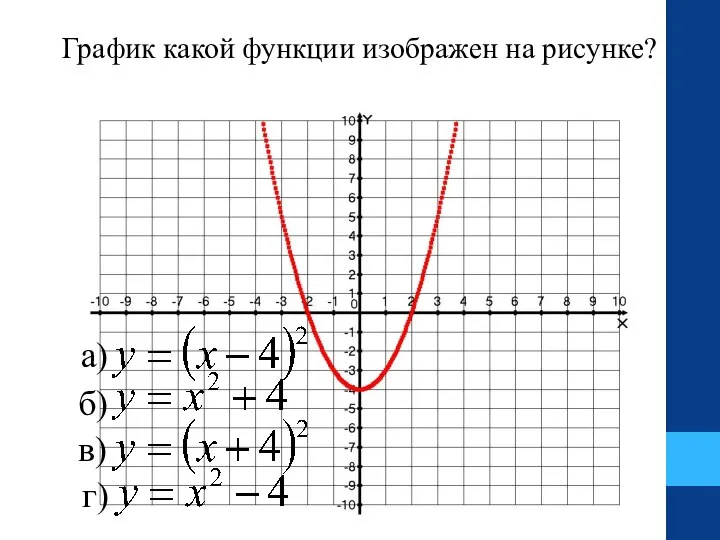
- 24. График какой функции изображен на рисунке? а) б) в) г)
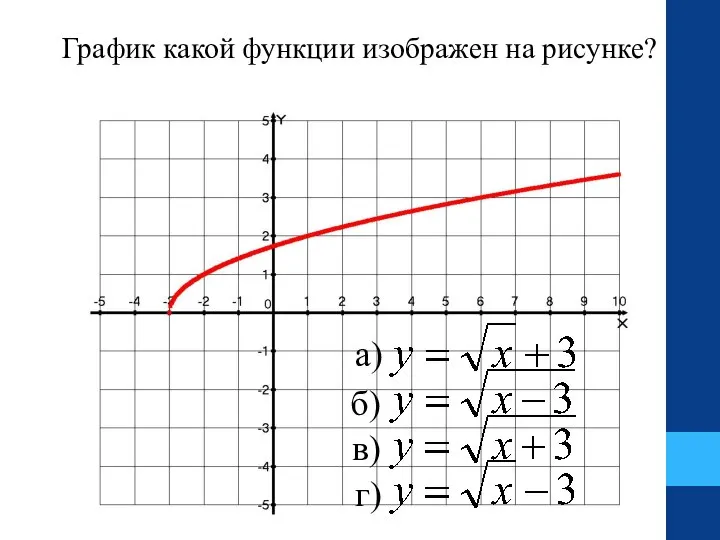
- 25. График какой функции изображен на рисунке? а) б) в) г)
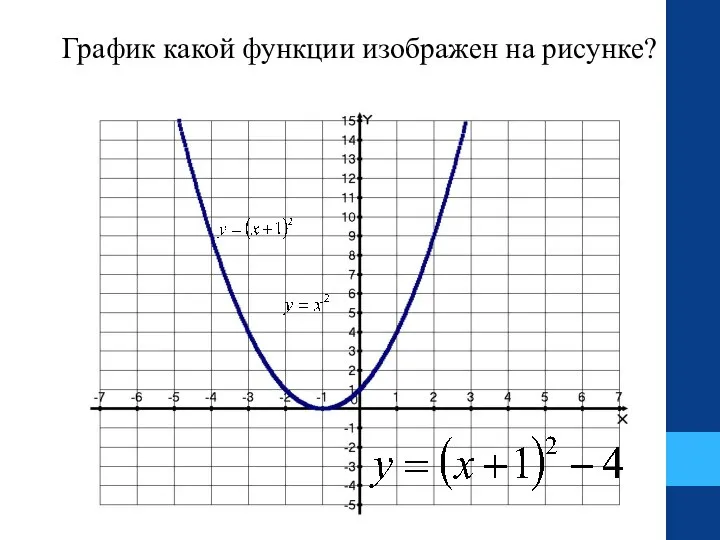
- 26. График какой функции изображен на рисунке?
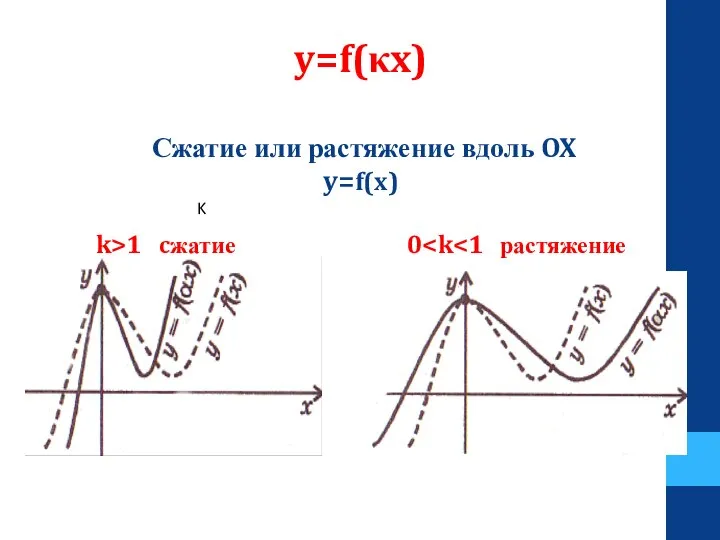
- 27. y=f(κx) Сжатие или растяжение вдоль OX y=f(x) k>1 cжатие 0 K
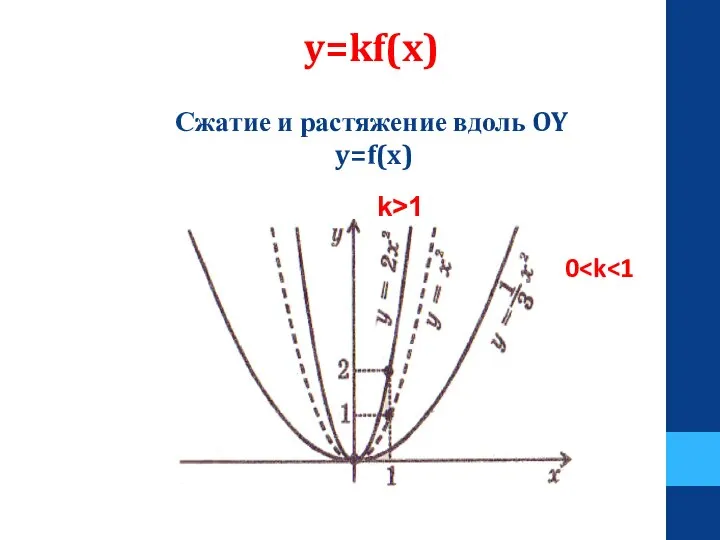
- 28. y=kf(x) Сжатие и растяжение вдоль OY y=f(x) 0 k>1
- 30. Скачать презентацию










 Частное и его значение
Частное и его значение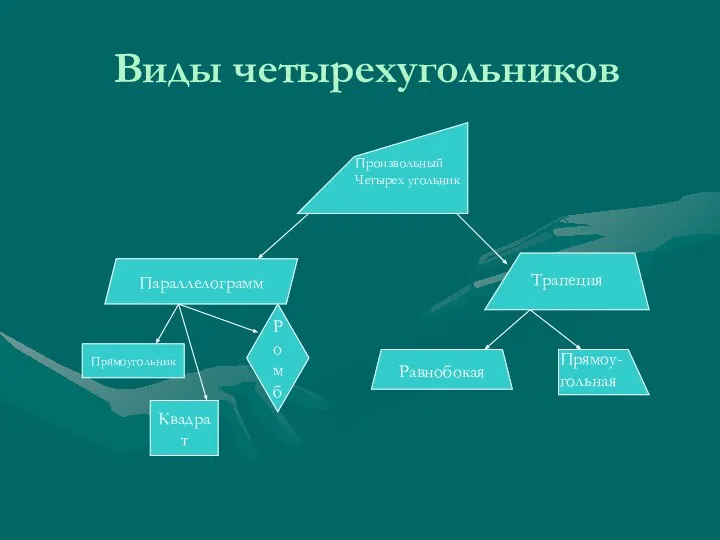 Виды четырехугольников
Виды четырехугольников Процентное содержание компонентов
Процентное содержание компонентов Окружность
Окружность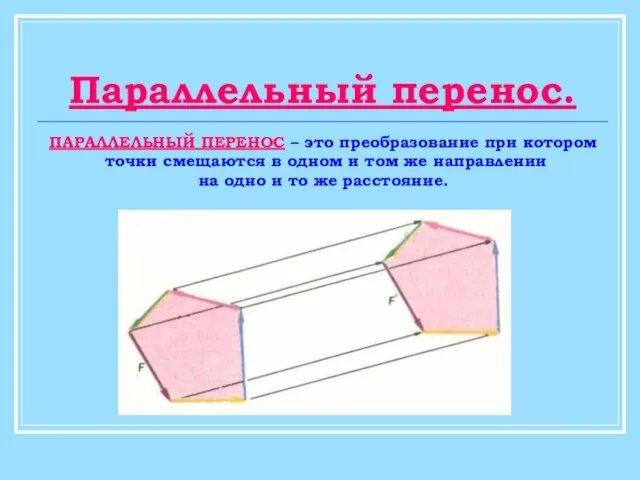 Параллельный перенос фигур
Параллельный перенос фигур Сущность экономического прогнозирования
Сущность экономического прогнозирования первые уроки геометрии
первые уроки геометрии Показательные неравенства
Показательные неравенства Стандартный вид числа
Стандартный вид числа Таблица сложения
Таблица сложения Окружность, круг, их элементы и части. Центральный угол. 7 класс
Окружность, круг, их элементы и части. Центральный угол. 7 класс Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов
Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов Какую прямую называют координатной?
Какую прямую называют координатной? Решение задач с помощью уравнений. Урок математики в 5 классе
Решение задач с помощью уравнений. Урок математики в 5 классе Презентация на тему Теорема синусов
Презентация на тему Теорема синусов  Теорема о неполноте
Теорема о неполноте Презентация на тему Технологии развивающего обучения в практике учителя математики
Презентация на тему Технологии развивающего обучения в практике учителя математики  Подготовка к ЕГЭ. Графическое решение уравнений и неравенств
Подготовка к ЕГЭ. Графическое решение уравнений и неравенств Проект Математическая вертикаль. Геометрия. 8 класс
Проект Математическая вертикаль. Геометрия. 8 класс Задача з піцою
Задача з піцою Презентация на тему Место числового множителя в выражении с переменной
Презентация на тему Место числового множителя в выражении с переменной  Разложение функций в степенные ряды
Разложение функций в степенные ряды Иррациональные уравнения
Иррациональные уравнения Умножение
Умножение Геометрия в искусстве
Геометрия в искусстве Что такое дискретная математика?
Что такое дискретная математика? Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график
Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график סדר פעולות החשבון
סדר פעולות החשבון