Содержание
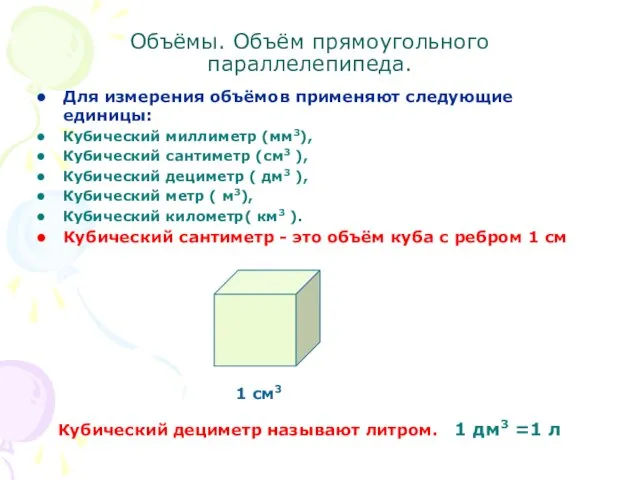
- 2. Объёмы. Объём прямоугольного параллелепипеда. Для измерения объёмов применяют следующие единицы: Кубический миллиметр (мм3), Кубический сантиметр (см3
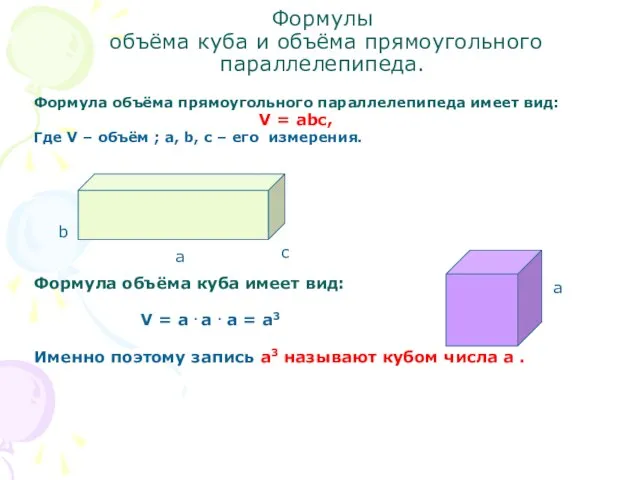
- 3. Формула объёма прямоугольного параллелепипеда имеет вид: V = abc, Где V – объём ; a, b,
- 4. Старинные единицы объёма На Руси в старину использовались в качестве единиц измерения объёма ведро ( 12
- 5. В обиходе, два ведра на коромысле должны быть в "подъём женщине". Деление на более мелкие меры
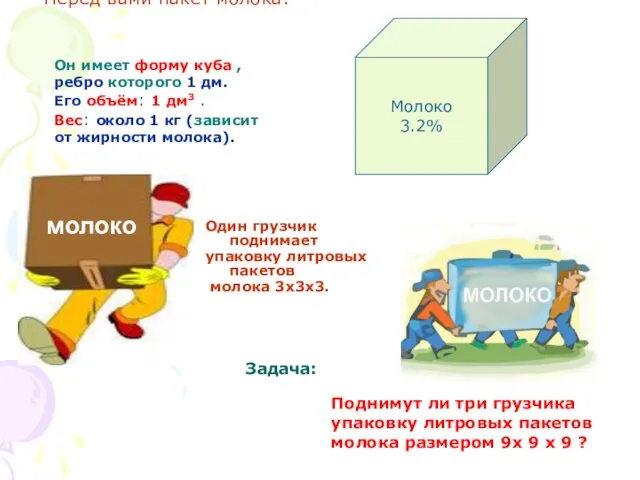
- 6. Перед вами пакет молока: Один грузчик поднимает упаковку литровых пакетов молока 3х3х3. Молоко 3.2% Он имеет
- 7. Решение: Количество пакетов молока первой упаковки: 3 х 3 х 3 = 27 (пакетов) Объём первой
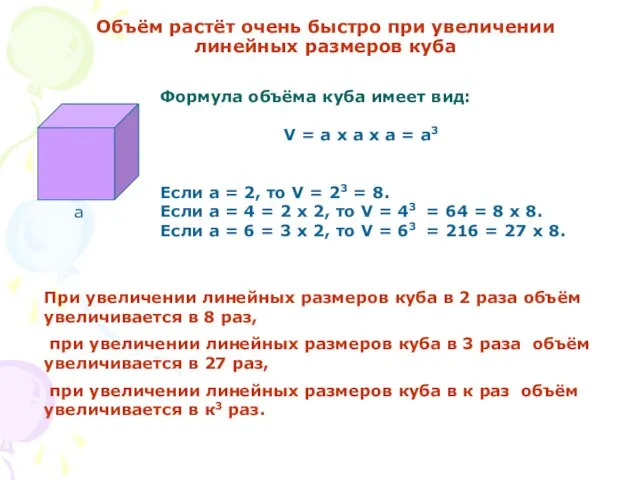
- 8. Объём растёт очень быстро при увеличении линейных размеров куба а Формула объёма куба имеет вид: V
- 9. Он тяжелый и пузатый, Носит фрак свой полосатый. На макушке хвостик-ус, спелый изнутри … Задача: Вам
- 10. Этот арбуз с тонкой корочкой Стоит 100 рублей ∠
- 11. А этот арбуз с толстой корочкой и 20% его радиуса придется выкинуть Он стоит 70 рублей
- 12. Их радиусы одного диаметра
- 13. Какой арбуз выгоднее купить?
- 14. Решение: Арбуз имеет форму шара. Объём шара находим по формуле: V = 4/3πR3 Пусть радиус первого
- 16. Скачать презентацию









 Комплексные числа и действия над ними
Комплексные числа и действия над ними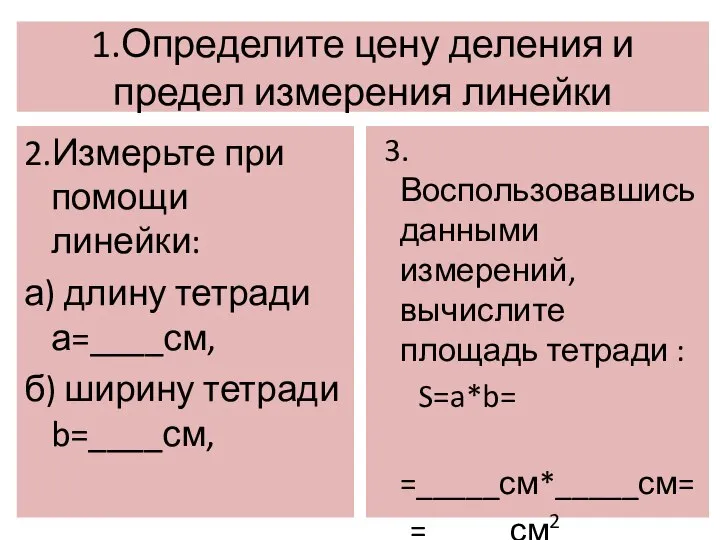 Цена деления и предел измерения линейки
Цена деления и предел измерения линейки Состав чисел
Состав чисел Умножение десятичных дробей. Графический диктант
Умножение десятичных дробей. Графический диктант Властивості і графіки тригонометричних функцій. Графік тангенса та котангенса числового аргументу
Властивості і графіки тригонометричних функцій. Графік тангенса та котангенса числового аргументу Реши уравнения
Реши уравнения Числоа 6, 7. Письмо цифры 6
Числоа 6, 7. Письмо цифры 6 Треугольники
Треугольники Теорема Виета. Урок систематизации, обобщения и контроля знаний
Теорема Виета. Урок систематизации, обобщения и контроля знаний Презентация на тему Метод интервалов
Презентация на тему Метод интервалов  Решение уравнений с одной переменной
Решение уравнений с одной переменной Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений Признаки параллельности прямых
Признаки параллельности прямых Умножение и деление отрицательных чисел. Урок-путешествие
Умножение и деление отрицательных чисел. Урок-путешествие Преобразование графиков вида у=f(х±а)
Преобразование графиков вида у=f(х±а) Математика. Числа до 20
Математика. Числа до 20 Какой функции соответствует график
Какой функции соответствует график Контрольная работа
Контрольная работа Теория антагонистических игр. Задачи для выполнения
Теория антагонистических игр. Задачи для выполнения Интерактивный тренажёр Весёлый счёт. Математика 1 класс
Интерактивный тренажёр Весёлый счёт. Математика 1 класс Задачи на перебор вариантов
Задачи на перебор вариантов Решение тригонометрических уравнений
Решение тригонометрических уравнений Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого Дифференциальные уравнения высшего порядка
Дифференциальные уравнения высшего порядка Итогово-обобщающий урок. Площадь. Теорема Пифагора
Итогово-обобщающий урок. Площадь. Теорема Пифагора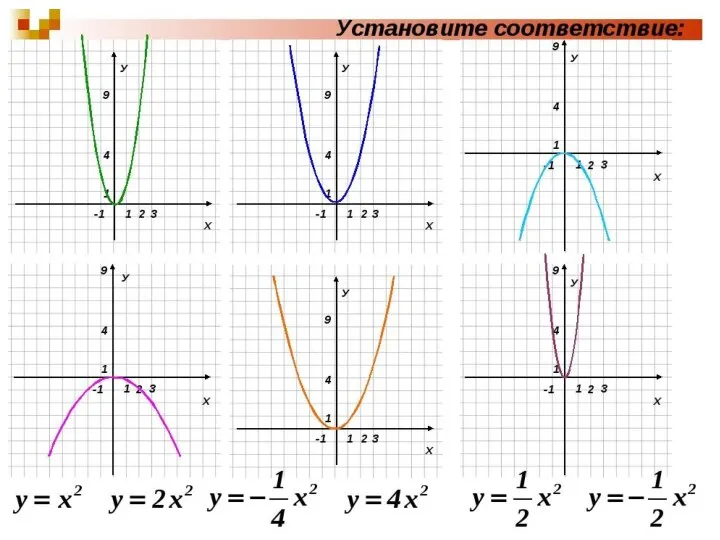 Графики функций
Графики функций Результант. Литература
Результант. Литература Занятие 45. Формулы двойного угла. Формулы половинного угла
Занятие 45. Формулы двойного угла. Формулы половинного угла