Многогранники. Вершины, рёбра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера

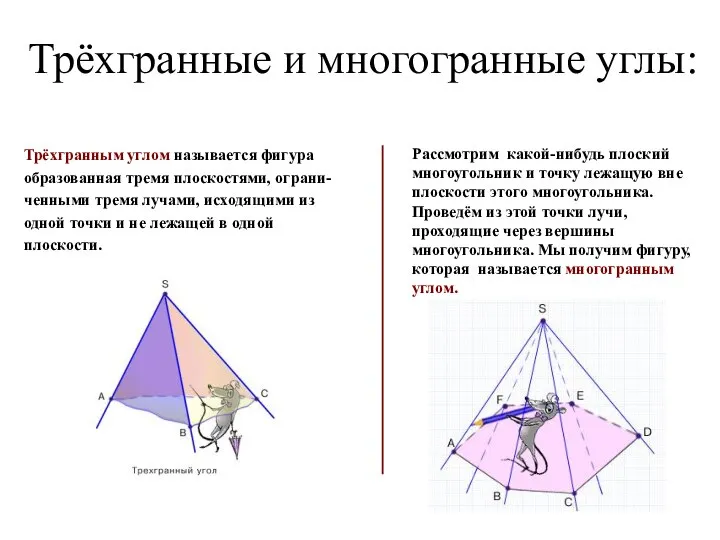
Трёхгранные и многогранные углы:
Трёхгранным углом называется фигура
образованная тремя плоскостями, ограни-
ченными тремя лучами, исходящими из
одной точки и не лежащей в одной
плоскости.
Рассмотрим какой-нибудь плоский многоугольник и точку лежащую вне плоскости этого многоугольника. Проведём из этой точки лучи, проходящие через вершины многоугольника. Мы получим фигуру, которая называется многогранным углом.

Трёхгранный угол — это часть пространства, ограниченная тремя плоскими углами с общей вершиной и попарно общими сторонами, не лежащими в одной плоскости. Общая вершина О этих углов называется вершиной трёхгранного угла. Стороны углов называются рёбрами, плоские углы при вершине трёхгранного угла называются его гранями. Каждая из трёх пар граней трёхгранного угла образует двугранный угол

Основные свойства трехгранного угла
1. Каждый плоский угол трёхгранного угла меньше суммы двух других его плоских углов.
α + β > γ; α + γ > β; β + γ > α
2. Сумма плоских углов трёхгранного угла меньше 360 градусов
α, β, γ — плоские углы,
A, B, C — двугранные углы, составленные плоскостями углов β и γ, α и γ, α и β.
3. Первая теорема косинусов
для трёхгранного угла
4. Вторая теорема косинусов для трёхгранного угла

,
5. Теорема синусов
Многогранный угол, внутренняя область которого расположена по одну сторону от плоскости каждой из его граней, называется выпуклым многогранным углом. В противном случае многогранный угол называется невыпуклым.

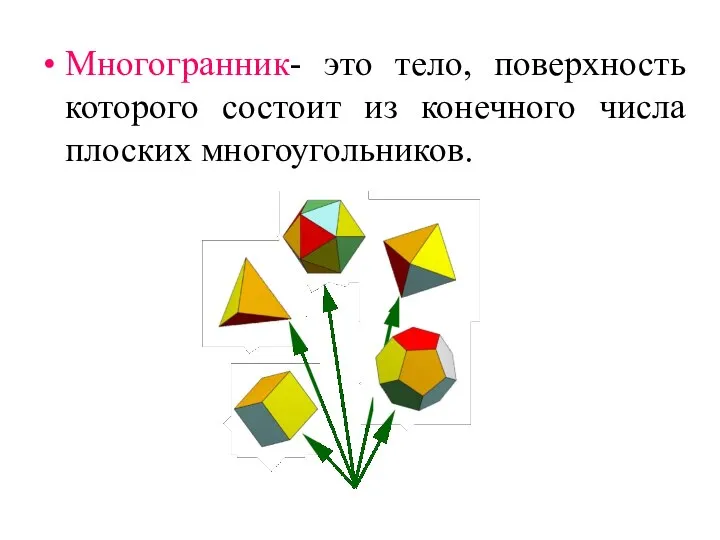
Многогранник- это тело, поверхность которого состоит из конечного числа плоских многоугольников.

Грани многогранника - это многоугольники, которые его образуют.
Ребра многогранника - это стороны многоугольников.
Вершины многогранника - это вершины многоугольника.
Диагональ многогранника - это отрезок, соединяющий 2 вершины, не принадлежащие одной грани.
Элементы многогранника

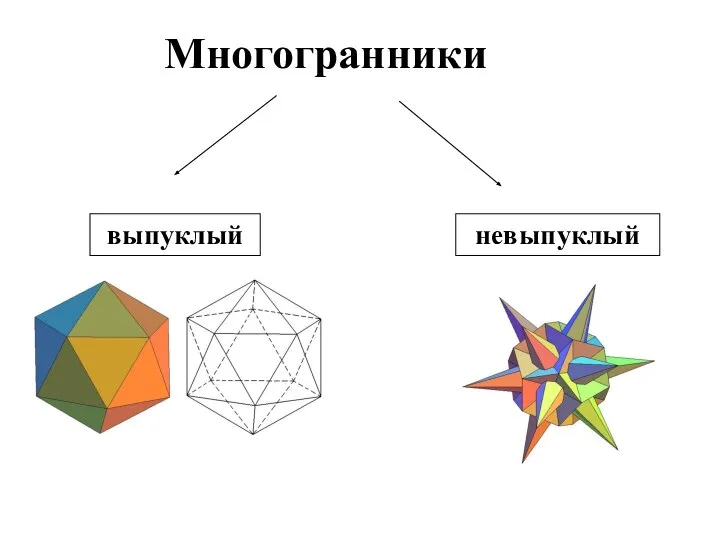
выпуклый
невыпуклый
Многогранники

Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого многоугольника на его поверхности.

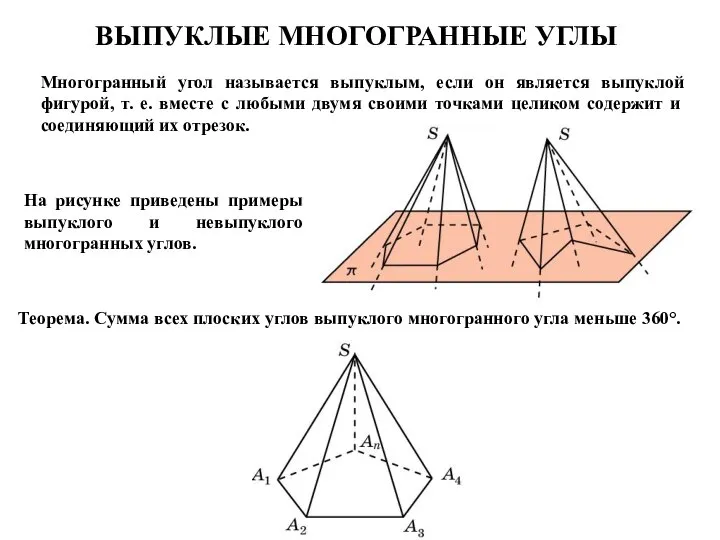
ВЫПУКЛЫЕ МНОГОГРАННЫЕ УГЛЫ
Многогранный угол называется выпуклым, если он является выпуклой фигурой, т. е. вместе с любыми двумя своими точками целиком содержит и соединяющий их отрезок.
На рисунке приведены примеры выпуклого и невыпуклого многогранных углов.
Теорема. Сумма всех плоских углов выпуклого многогранного угла меньше 360°.

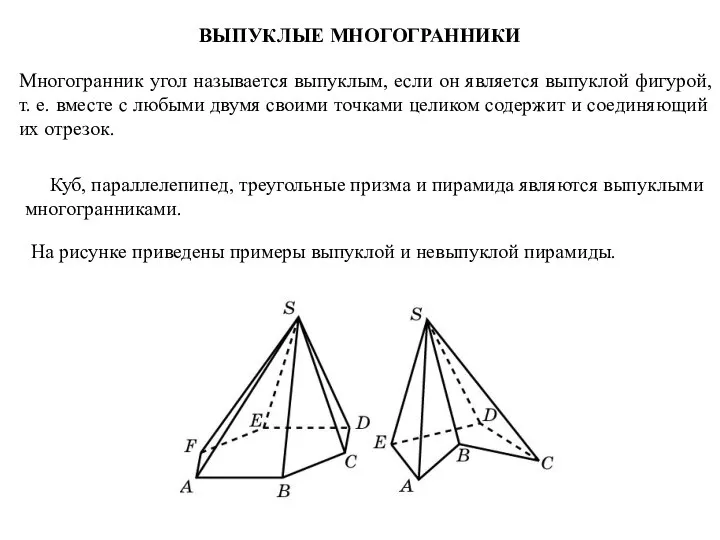
ВЫПУКЛЫЕ МНОГОГРАННИКИ
Многогранник угол называется выпуклым, если он является выпуклой фигурой, т. е. вместе с любыми двумя своими точками целиком содержит и соединяющий их отрезок.
На рисунке приведены примеры выпуклой и невыпуклой пирамиды.
Куб, параллелепипед, треугольные призма и пирамида являются выпуклыми многогранниками.

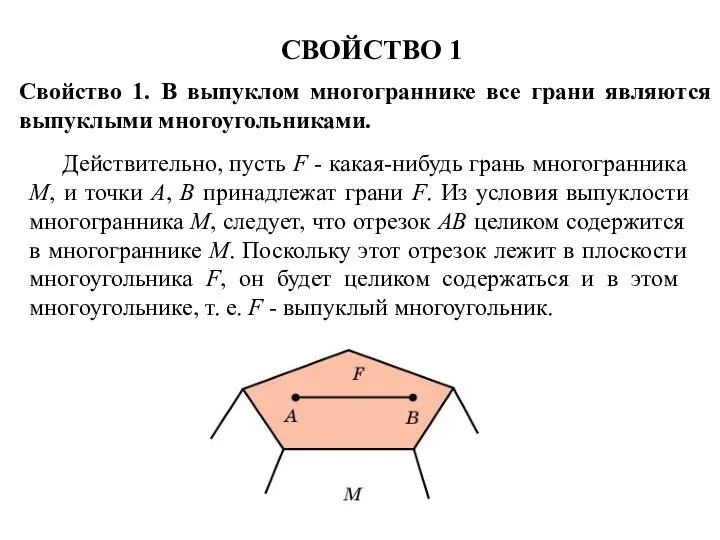
СВОЙСТВО 1
Свойство 1. В выпуклом многограннике все грани являются выпуклыми многоугольниками.
Действительно, пусть F - какая-нибудь грань многогранника M, и точки A, B принадлежат грани F. Из условия выпуклости многогранника M, следует, что отрезок AB целиком содержится в многограннике M. Поскольку этот отрезок лежит в плоскости многоугольника F, он будет целиком содержаться и в этом многоугольнике, т. е. F - выпуклый многоугольник.

СВОЙСТВО 2
Действительно, пусть M - выпуклый многогранник. Возьмем какую-нибудь внутреннюю точку S многогранника M, т. е. такую его точку, которая не принадлежит ни одной грани многогранника M. Соединим точку S с вершинами многогранника M отрезками. Заметим, что в силу выпуклости многогранника M, все эти отрезки содержатся в M. Рассмотрим пирамиды с вершиной S, основаниями которых являются грани многогранника M. Эти пирамиды целиком содержатся в M, и все вместе составляют многогранник M.
Свойство 2. Всякий выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника.

Правильные многогранники
Если грани многогранника являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер, то выпуклый многогранник называется правильным.

пришли из Древней Греции,
в них указывается число граней:
«эдра» − грань;
«тетра» − 4;
«гекса» − 6;
«окта» − 8;
«икоса» − 20;
«додека» − 12.
Названия многогранников

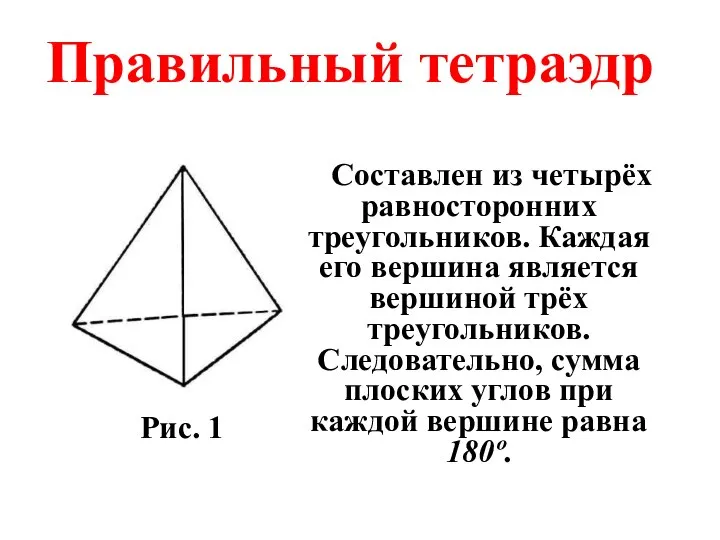
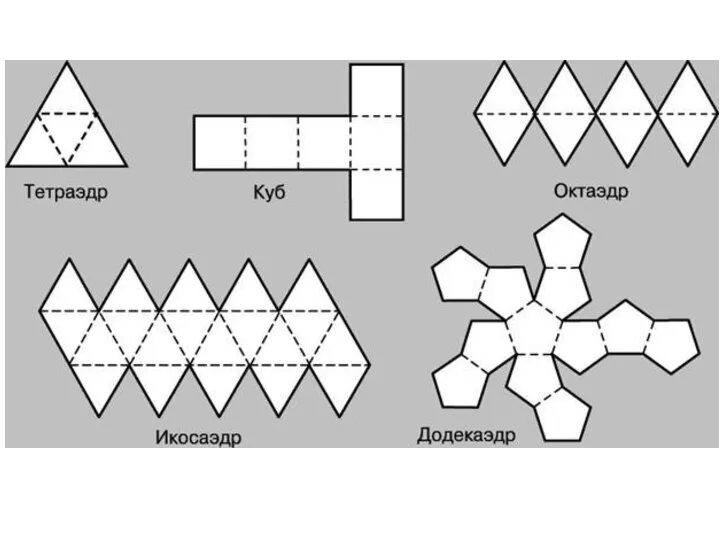
Правильный тетраэдр
Составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180º.
Рис. 1

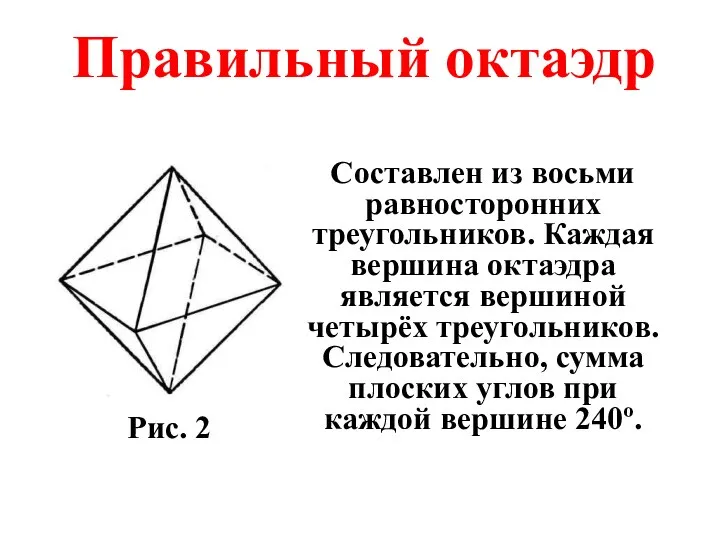
Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников. Следовательно, сумма плоских углов при каждой вершине 240º.
Правильный октаэдр
Рис. 2

Правильный икосаэдр
Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300º.
Рис. 3

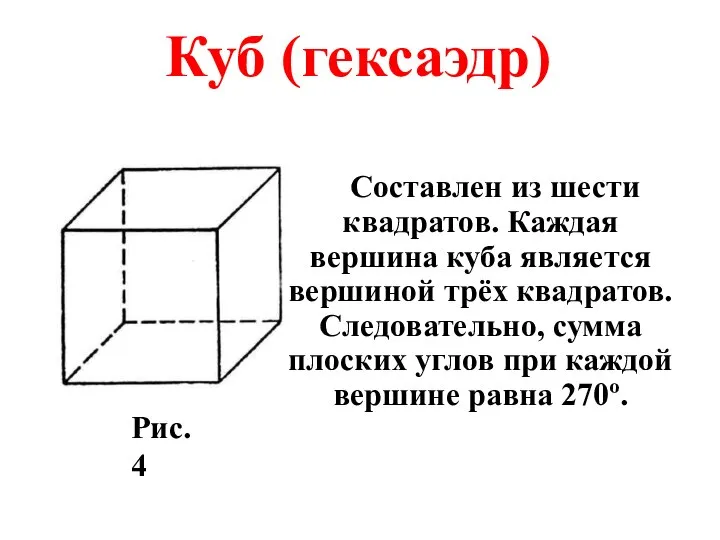
Составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270º.
Куб (гексаэдр)
Рис. 4

Правильный додекаэдр
Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324º.
Рис. 5

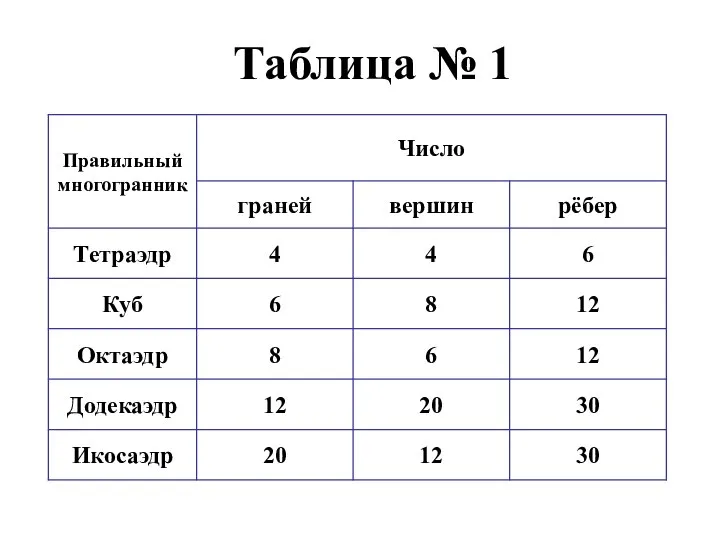
Таблица № 1

Сумма числа граней и вершин любого многогранника
равна числу рёбер, увеличенному на 2.
Г + В = Р + 2
Формула Эйлера
Число граней плюс число вершин минус число рёбер
в любом многограннике равно 2.
Г + В − Р = 2

Таблица № 2

Двойственность правильных многогранников
Гексаэдр (куб) и октаэдр образуют двойственную пару многогранников. Число граней одного многогранника равно числу вершин другого и наоборот.

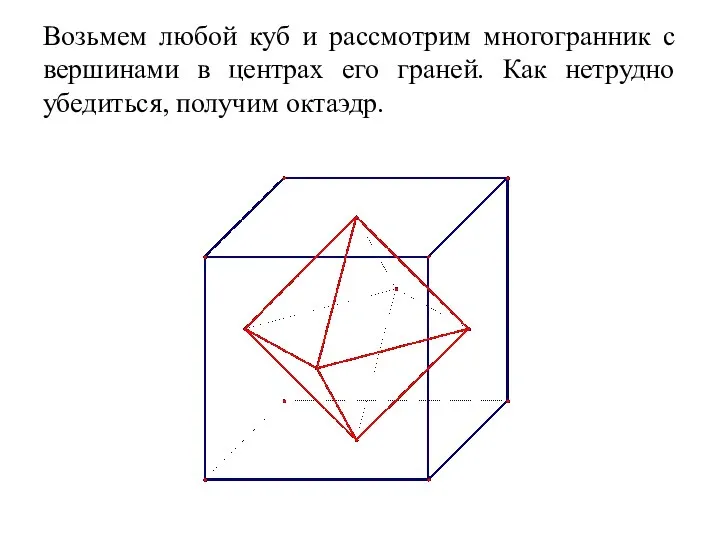
Возьмем любой куб и рассмотрим многогранник с вершинами в центрах его граней. Как нетрудно убедиться, получим октаэдр.

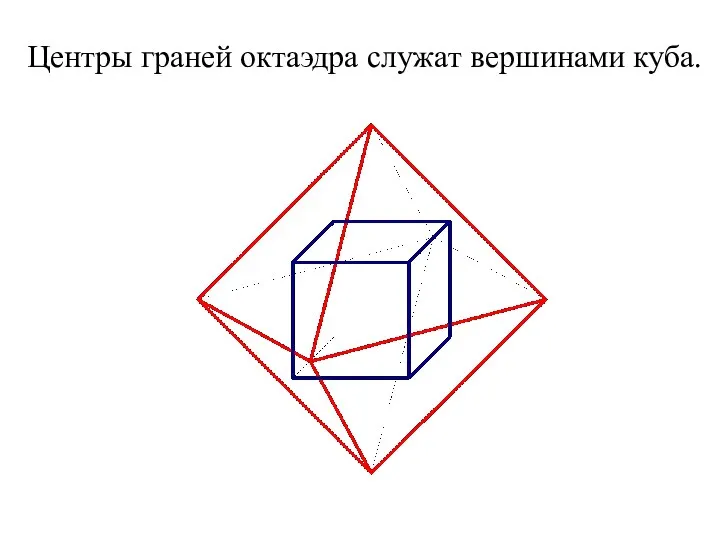
Центры граней октаэдра служат вершинами куба.

Сурьменистый сернокислый натрий – тетраэдра.
Многогранники в природе, химии и биологии
Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников.
Кристалл пирита— природная модель додекаэдр.
Кристаллы поваренной соли передают форму куб.
Монокристалл алюминиево-калиевых квасцов имеет форму октаэдра.
Хрусталь (призма)
Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень - икосаэдр.
В процессе деления яйцеклетки сначала образуется тетраэдр из четырех клеток, затем октаэдр, куб и, наконец, додекаэдро-икосаэдрическая структура гаструлы. И наконец, самое, пожалуй, главное – структура ДНК генетического кода жизни – представляет собой четырехмерную развертку (по оси времени) вращающегося додекаэдра!
В молекуле метана имеет форму правильного тетраэдра.

Многогранники в искусстве
«Портрет Монны Лизы»
Композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника.
гравюра «Меланхолия»
На переднем плане картины изображен додекаэдр.
«Тайная Вечеря»
Христос со своими учениками изображён на фоне огромного прозрачного додекаэдр.