Содержание
- 2. Этими физическими свойствами зеркал и воспользовались великий Архимед и Маршал Жуков при ведении боевых действий История
- 3. Из книги Г. К. Жукова «Воспоминания и размышления»: «Так родилась идея ночной атаки с применением прожекторов
- 4. Дифференциальные уравнения высших порядков. 1. Дифференциальные уравнения 2-го порядка. Определение. Уравнения вида называются дифференциальными уравнениями 2-го
- 5. Лемма. Дифференциальное уравнение 2-го порядка обычно имеет бесчисленное множество решений, определяемых формулой содержащей две произвольные постоянные.
- 6. Пример. Геометрический смысл начальных условий: Помимо точки задаем угловой коэффициент касательной.
- 7. Теорема о существовании и единственности решения. Если функция и ее производные непрерывны в окрестности значений то
- 8. Из теоремы следует, что уравнение при заданных начальных условиях имеет единственное решение. Если задать начальные условия
- 9. Пример.
- 10. 2. Частные случаи дифференциальных уравнений 2-го порядка. 1) Правая часть не содержит и интегрируем дважды
- 11. 2) Правая часть не содержит Замена Это дифференциальное уравнение 1-го порядка. Пример.
- 12. 3) Правая часть не содержит Введем замену Таким образом - дифференциальное уравнение 1-ого порядка, общим решением
- 14. Пример
- 15. Пример 1.
- 16. Пример 2. Найти частное решение уравнения удовлетворяющее начальным условиям: хо= 0, уо= 0, у/о= 1.
- 17. Пример 2. Найти частное решение уравнения удовлетворяющее начальным условиям: хо= 0, уо= 0, у/о= 1.
- 18. Пример 2. Найти частное решение уравнения удовлетворяющее начальным условиям: хо= 0, уо= 0, у/о= 1.
- 19. Пример 2. Найти частное решение уравнения удовлетворяющее начальным условиям: хо= 0, уо= 0, у/о= 1.
- 21. Пример 3. Найти общее решение ДУ2 : уу// - 2(у/)2=0. Решение. Уравнение явно не содержит х.
- 22. Пример 3. Найти общее решение ДУ2 : уу// - 2(у/)2=0. Решение. Уравнение явно не содержит х.
- 23. Пример 3. Решение. Уравнение явно не содержит х. Найти общее решение ДУ2 : уу// - 2(у/)2=0.
- 28. Скачать презентацию







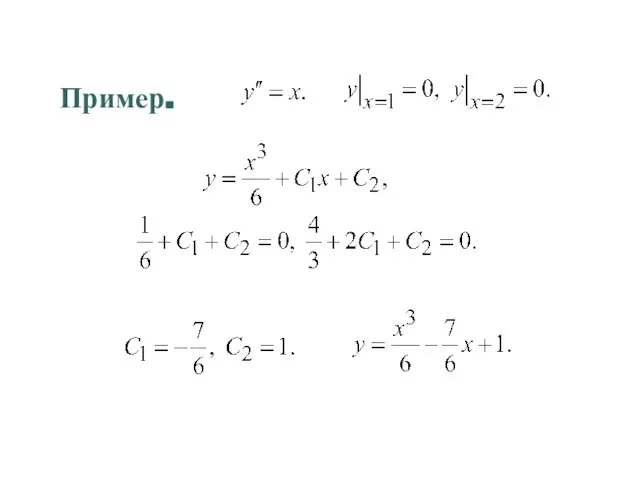

















 Арифметические действия
Арифметические действия Таблица значений синуса, косинуса, тангенса для углов
Таблица значений синуса, косинуса, тангенса для углов Логарифмическая линейка
Логарифмическая линейка Синус, косинус, тангенс и котангенс угла поворота
Синус, косинус, тангенс и котангенс угла поворота Конус. Цилиндр. Сфера
Конус. Цилиндр. Сфера Случаи вычитания 15 -
Случаи вычитания 15 - Средства измерений, классификация. Метрологические характеристики средств измерений
Средства измерений, классификация. Метрологические характеристики средств измерений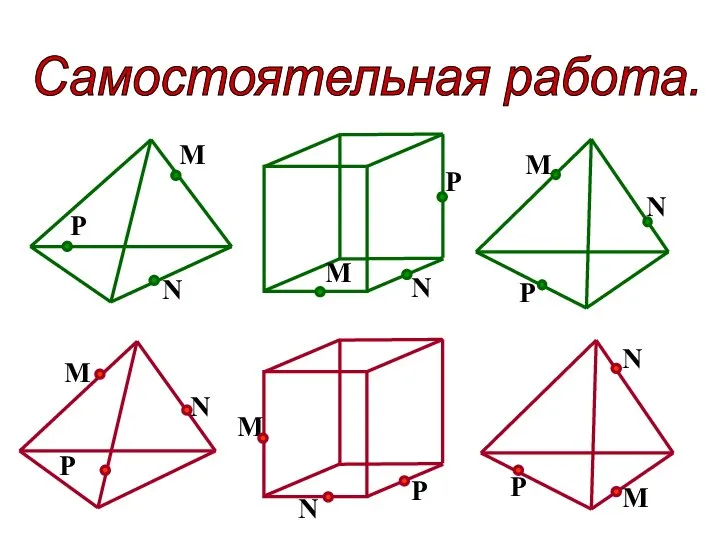 Построение сечений многогранников
Построение сечений многогранников Вычисление углов между прямыми и плоскостями
Вычисление углов между прямыми и плоскостями Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Анализ геометрической формы предмета
Анализ геометрической формы предмета Четырехугольник и его элементы
Четырехугольник и его элементы Касательная к окружности. Свойства касательных к окружности. 7 класс
Касательная к окружности. Свойства касательных к окружности. 7 класс Упрощение выражений. Восстановите цепочку вычислений
Упрощение выражений. Восстановите цепочку вычислений Призма. Площади поверхностей. Объем призмы
Призма. Площади поверхностей. Объем призмы Системы координат, используемые в спутниковых измерениях
Системы координат, используемые в спутниковых измерениях Графики
Графики Линейная алгебра просто! интерактивное учебное пособие
Линейная алгебра просто! интерактивное учебное пособие Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Умножение одночленов. Возведение одночлена в степень
Умножение одночленов. Возведение одночлена в степень Хитрые задачи. 4 класс
Хитрые задачи. 4 класс Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Геометрическая прогрессия. Урок 1
Геометрическая прогрессия. Урок 1 Умножение натуральных чисел
Умножение натуральных чисел Цветочное настроение. Математика
Цветочное настроение. Математика Уравнение сферы
Уравнение сферы Равнобедренный треугольник. Окружность
Равнобедренный треугольник. Окружность Метод координат
Метод координат